Fließproduktionssysteme mit begrenzten Puffern und konstanter Anzahl von Werkstückträgern
In der betrieblichen Praxis findet man nicht selten Fließproduktionssysteme, in denen nur eine begrenzte Anzahl von Werkstückträgern (bzw. Paletten, Skids, etc.) zirkuliert. Das sieht dann so aus:
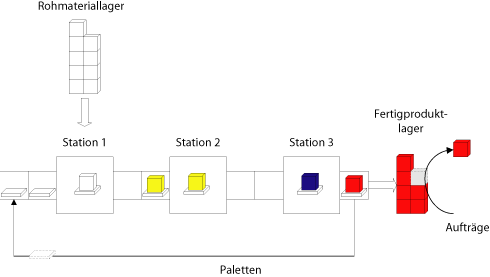
In dem System zirkulieren $N=7$ Paletten. An Station 1 wird ein unbearbeitetes Werkstück aus dem Rohmateriallager entnommen und auf eine leere Palette montiert. (Das Rohmateriallager ist oft das "Fertigproduktlager" aus der Sicht einer vorgelagerten Produktionsprozesses.) Nach Abschluß der Bearbeitung an Station 3 wird ein fertiges Werkstück von der Palette entfernt und die Palette wieder an den Systemanfang zurückgeschickt. Vernachlässigt man die Transferzeit vom Systemende zum Systemanfang und die Zeitspanne, die die leere Palette vor Station 1 auf das Aufspannen des nächsten Werkstücks wartet, dann ist der Lagerbestand in einem solchen System immer gleich der Anzahl Werkstückträger, $N$.
Solche Systeme nennt man auch geschlossene Systeme oder Systeme mit Bestandskontrolle.
Im Unterschied zu einem offenen System kann bei einem geschlossenen Werkstückträgerumlauf die erste Station in gleicher Weise wie alle anderen Stationen unter Materialmangel leiden und die letzte Station kann blockiert sein. Dies tritt dann häufig auf, wenn der Puffer zwischen der letzten Station $M$ und der ersten Station relativ klein ist. Dies wiederum ist oft der Fall, wenn die Stationen U-förmig angeordnet sind.
Ein System mit geschlossenen Werkstückträgerumlauf kann nicht produktiver sein als das äquivalente offene System.
Ist der kleinste Puffer größer als die Anzahl von Werkstückträgern $N$, dann kann es niemals zu Blockierungen kommen. In diesem Fall kann man das System als ein geschlossenes Warteschlangennetzwerk mit unbegrenzten Puffern modellieren, wie es z.B. auch für die Analyse des CONWIP-Systems oder von Flexiblen Fertigungssystemen eingesetzt wird.
Bei unbeschränkten Puffern und begrenzter Anzahl Paletten ist festzustellen, daß die Produktionsrate eine degressiv ansteigende Funktion der Anzahl Paletten ist. Ist ein bestimmtes Sättigungsniveau (Anzahl Paletten) erreicht, dann erhöhen zusätzliche Paletten nur noch den Lagerbestand. Sie bewirken aber keine weitere Erhöhung der Produktionsrate. Denn der Engpaß des Systems ist voll ausgelastet. Diese Annahme trifft man z.B. bei der Analyse eines Flexiblen Fertigungssystems in der statischen Analyse eines geschlossenen Warteschlangennetzwerks.
Anders ist es bei beschränkten Puffern und begrenzter Anzahl Paletten. In diesem Fall steigt die Produktionsrate zunächst an, nimmt aber ab einer bestimmten Anzahl Paletten wieder ab. Wird der gesamte Platz im System durch die zahl der Paletten überschritten, dann kommt es sogar zu einem Systemstillstand. In jedem Fall hat die Anzahl Werkstückträger $N$ einen erheblichen Einfluß auf die Produktionsrate des Systems. Ist $N$ zu niedrig, dann kommt nicht nur an den Stationen 2 bis $M$, sondern auch an Station 1 zu Materialmangel. Ist z.B. $N$ kleiner als die Anzahl Stationen, $M$, dann ist immer mindestens eine Station nicht beschäftigt. Dies führt zwangsläufig zu einem Produktionsmengenverlust im Vergleich zu der Situation, in der genügend Werkstückträger zirkulieren, um den Engpaß des Systems immer zu beschäftigen. Ist $N$ größer als der Puffer zwischen den Stationen $M$ und $1$, dann kann es auch an der letzten Station zu Blockierungen kommen. Im Extremfall, wenn $N$ gleich dem gesamten Speicherplatz im System (Summe aus allen Pufferplätzen und allen Bearbeitungsplätzen an den Stationen) ist, dann kommt es zu einem Systemstillstand (deadlock), da dann nichts mehr geht. Eine Obergrenze für die Anzahl Werkstückträger ist somit $\sum_{m=1}^{M}$(Pufferplätze+Bearbeitungsplätze) -1.
Das folgende Bild zeigt die Entwicklung der Produktionsrate eines 20-Stationen-Systems mit stochastischen Bearbeitungszeiten mit identischen Mittelwerten und Variationskoeffizienten von 0.3 als Funktion der Anzahl Werkstückträger. Die Puffer vor den Stationen können 2 Paletten aufnehmen.
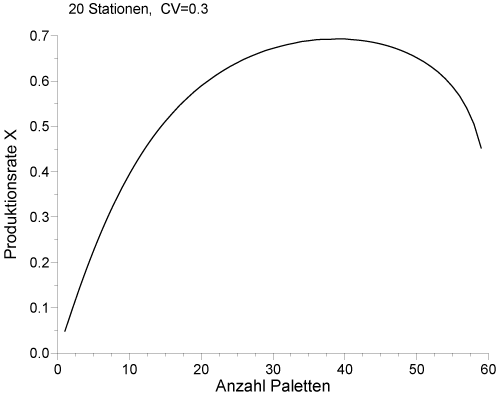
Die Produktionsrate steigt zunächst an, nimmt ab einer bestimmten Anzahl Paletten aber wieder ab. Je nachdem, wie groß die Puffer zwischen den Stationen sind, ist der flache Bereich der Produktionsfunktion schmaler oder breiter. Bei großen Puffern gibt es auch einen Bereich, in dem die Produktionsfunktion parallel zur X-Achse verläuft.
Ökonomisch relevant, d.h. effizient ist nur der linke Teil der Produktionsfunktion bis zum Maximalwert der Produktionsrate. Erhöht man $N$ über $N(X_{max})$ hinaus, dann führen zusätzliche Werkstückträger zu einem Rückgang der Produktionsrate. Dies ist selbst dann nicht sinnvoll, wenn die Werkstückträger keine Kosten verursachen. Da allerdings ein Werkstückträger i.d.R. mit Kosten verbunden ist - es gibt Paletten, die mehrere Tausend Euro kosten - , ist lediglich die linke Hälfte der Produktionsfunktion $N \leq N(X_{max})$ für Optimierungszwecke relevant.
Ist das System linear aufgebaut (und nicht kreis- oder U-förmig), dann ist der Transportweg für die Rückführung der leeren Paletten zum Systemanfang so lang wie das gesamte System. In diesem Fall kann es sein, daß der Puffer vor der Station 1 schon aus baulichen Gründen so groß ist, daß er niemals voll wird. In einem solchen System nähert sich die Produktionsrate als Funktion der Anzahl Paletten einer oberen Schranke (ähnlich wie in einem offenen System mit unbegrenzter Anzahl von Werkstückträgern). Dies zeigt das folgende Bild:
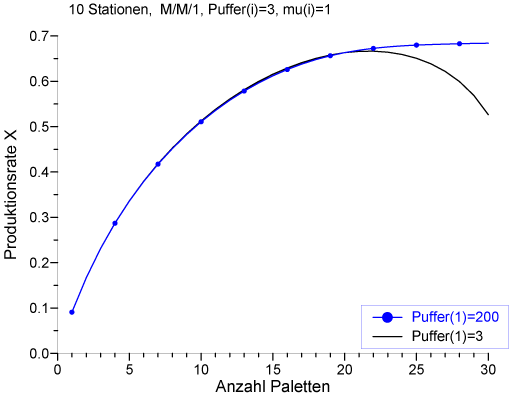
In dem betrachteten 10-Stationen-System sind die Bearbeitungszeiten an allen Stationen exponentialverteilt. Alle Puffergrößen sind identisch gleich 3. Variiert wurde der Puffer vor Station 1. Man erkennt, daß für den Fall eines unbeschränkten Puffers vor Station 1 die Produktionsrate sich einer oberen Schranke annähert.
Für die Optimierung eines Fließproduktionssystems mit begrenzter Anzahl von Werkstückträgern sind nun folgende Fragen von Interesse:
- Wie viele Puffer werden benötigt, um eine angestrebte Produktionsrate zu erreichen?
- Wie sollen diese Puffer auf die Stationen verteilt werden?
- Wie viele Paletten bzw. Werkstückträger sollen in dem System zirkulieren?
Zwischen diesen Fragen bestehen Interdependenzen. So hängt die optimale Gesamtanzahl von Pufferplätzen von der Pufferverteilung ab. Sind die Puffergrößen (aus Kostengründen oder aufgrund technischer Restriktionen) begrenzt, dann hat dies Einfluß auf die Anzahl Werkstückträger.
Siehe auch ...
- Produktions-Management-Trainer
- Leistungsanalyse eines Fließproduktionssystems
- Analyse eines 2-Stationen-Systems mit begrenztem Puffer
- Analyse längerer Fließproduktionssysteme mit begrenzten Puffern
Literatur
| Günther, H.-O. und Tempelmeier, H. (2020). Supply Chain Analytics - Operations Management und Logistik. 13. Aufl., Norderstedt: Books on Demand. |
| Tempelmeier, H. (2020), Analytics in Supply Chain Management und Produktion - Übungen und Mini-Fallstudien. 7. Aufl., Norderstedt: Books on Demand. |