Analyse eines 2-Stationen-Systems mit begrenztem Puffer, erste Station niemals leer
Wir betrachten ein 2-Stationen-System mit den Stationen (1,2) bzw. ($m,m+1$) und wollen die Produktionsrate $X(m,m+1)$ dieses Systems bestimmen. Dieses 2-Stationen-System kann auch als ein Subsystem eines längeren Fließproduktionssystem mit begrenzten Puffern betrachtet werden. Daher die Notation ($m,m+1$).
Zur Analyse eines solchen 2-Stationen-Systems stehen verschiedene Modelle zur Verfügung, die von den speziellen Eigenschaften des realen Systems abhängen. Es gibt u.a. Modelle für folgende Systemtypen:
- exponential-verteilte Bearbeitungszeiten, keine Störungen
- allgemein-verteilte Bearbeitungszeiten, keine Störungen
- deterministische Bearbeitungszeiten, an allen Stationen identisch, Störungen
- deterministische Bearbeitungszeiten, stationsspezifisch, Störungen
Im einfachsten Fall gehen wir von folgenden Annahmen aus:
- 2 Stationen
- asynchroner Materialfluß
- an allen Stationen exponentialverteilte Bearbeitungszeiten
- keine Störungen
- Station 1 ist niemals unbeschäftigt, da der Materialnachschub unendlich schnell ist
- Station 2 ist niemals blockiert, das sie ein Werkstück nach Abschluß der Bearbeitung sofort weitergeben kann
Das betrachtete 2-Stationen-System kann wie folgt als Markow-Kette in kontinuierlicher Zeit mit diskreten Zuständen modelliert werden. Wir bezeichnen mit $\lambda$ die Bearbeitungsrate der Station 1 und mit $\mu$ die Bearbeitungsrate der Station 2 des Subsystems.
Gehen wir zunächst davon aus, daß die Größe des Puffers in dem Subsystem gleich $c=0$ ist. In diesem Fall sieht das System so aus:

Ein Zustand wird beschrieben durch die Anzahl $n$ von Werkstücken in dem Subsystem, die bereits an der Station 1, aber noch nicht an Station 2 bearbeitet worden sind. Die Anzahl der Zustände hängt also davon ab, wie viele Werkstücke an der Station 1 bereits bearbeitet worden sind, aber noch nicht die Station 2 passiert haben. Das sind
- $c$ Werkstücke im Puffer,
- 1 Werkstück an Station 2 in Bearbeitung und
- 1 Werkstück an Station 1, wenn diese blockiert wird,
also insgesamt $c+2$ Zustände. Hinzu kommt der Zustand, an dem kein Werkstück auf Station 2 wartet, diese also leer ist. D.h. die Anzahl der Zustände ist $c+3$. Ist die Pufferkapazität $c=0$, dann können folglich insgesamt 3 Zustände auftreten. Im vorliegenden Fall also:
$n$ |
Station 1 |
Puffer |
Station 2 |
0 |
arbeitet |
-- |
leer |
1 |
arbeitet |
-- |
arbeitet |
2 |
blockiert |
-- |
arbeitet |
Betrachten wir nun ein Subsystem mit zwei Pufferplätzen ($c=2$):
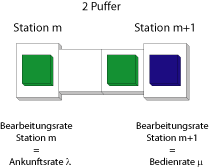
In diesem Fall gibt es $2+3=5$ Zustände, und zwar
$n$ |
Station 1 |
Puffer |
Station 2 |
0 |
arbeitet |
leer |
leer |
1 |
arbeitet |
leer |
arbeitet |
2 |
arbeitet |
1 Werkstück |
arbeitet |
3 |
arbeitet |
2 Werkstücke |
arbeitet |
4 |
blockiert |
2 Werkstücke |
arbeitet |
Das Gesamtsystem kann nicht leer sein, da Station 1 niemals unter Materialmangel leidet und somit immer entweder arbeitet oder blockiert ist. Zustandsveränderungen entstehen durch die "Bearbeitungsende"-Ereignisse an einer arbeitenden Station. Ist eine Station leer oder blockiert, dann tritt ein solches Ereignis nicht auf.
Zum Verständnis der weiteren Ausführungen zunächst einige allgemeine Bemerkungen. Wie erwähnt, kann das betrachtete 2-Stationen-System als ein Markov-Prozeß in kontinuierlicher Zeit mit diskreten Zuständen und stationären Übergangswahrscheinlichkeiten modelliert werden.
Dies ist ein stochastischer Prozeß $X(t)$ mit einer Zeitachse $t \in [0,\infty)$ und einer endlichen Menge von Zuständen $i=0,1, \ldots, I$, der folgende Eigenschaft hat:
$P\{X(t+h) = j\, |\, X(t) = i, X(s) = x(s), \forall s<t \} $
$= P\{X(t+h) = j\, |\, X(t) = i\}$
$= q_{ij} \cdot h + o(h)$
Das heißt, die bedingte Wahrscheinlichkeit dafür, daß im Zeitpunkt $t+h$ der Zustand $j$ eintritt, ist nur abhängig von dem Zustand im Zeitpunkt $t$, nicht aber davon, welche Zustände der Prozeß in der Vergangenheit, also in $s<t$ angenommen hatte. Darüberhinaus steigt diese bedingte Wahrscheinlichkeit linear mit der Länge der Zeitspanne $h$ mit dem Faktor $q_{ij}$, der als Übergangsrate (oder auch Intensität) bezeichnet wird. Diese wird weiter unten erläutert.
Die Wahrscheinlichkeiten
$p_{ij}(h) = P\{X(t+h) = j\, |\, X(t) = i\}$
nennt man Übergangswahrscheinlichkeiten zwischen dem Zustand $i$ und dem Zustand $j$ im Intervall $h$. Wenn diese unabhängig von der Länge des Zeitraums $h$ sind, dann spricht man von einer zeit-homogenen Markov-Kette.
Wir abstrahieren für einen Augenblick von dem zu analysierenden 2-Stationen-System und betrachten jetzt einen Markov-Prozeß, in dem die Zeitspanne, während der sich der Markov-Prozeß im Zustand $i$ befindet, mit der Rate $\nu_i$ exponentialverteilt sind. Angenommen, der Markov-Prozeß $X(t)$ befindet sich zum Zeitpunkt $t$ im Zustand $i$.
Wegen der Gedächtnislosigkeit der Exponentialverteilung ist dann die Wahrscheinlichkeit, daß der Prozeß diesen Zustand $i$ in einem bevorstehenden, sehr kurzen Zeitraum $h$ verläßt (z.B. daß die Bearbeitung an einem Werkstück abgeschlossen wird), gleich $\nu_i\cdot h + o(h)$. Dabei ist $o(h)$ eine Funktion, die für $h\rightarrow 0$ gegen 0 konvergiert.
Wenn der Prozeß den Zustand $i$ verläßt, dann erreicht er mit der Übergangswahrscheinlichkeit $p_{ij}$ den Zustand $j \neq i.$ Mit der Wahrscheinlichkeit $1-\nu_i\cdot h + o(h)$ bleibt der Prozeß weiterhin im Zustand $i$. Damit kann man schreiben (vgl. Tijms(1994), S. 132):
$P\{X (t, t + h) = j\,|\, X(t) = i\} = \nu_i \cdot h \cdot p_{ij} + o(h)$ , wenn $j\neq i$
$P\{X (t, t + h) = j\, |\, X(t) = i\} =1- \nu_i \cdot h + o(h)$, wenn $j=i$
für $h\rightarrow 0$. Da die Zeitspanne $h$ sehr klein ist, kann unterstellt werden, daß in $h$ immer nur ein Zustandsübergang auftritt. Übergänge $i\rightarrow k \rightarrow j$ kommen praktisch nicht vor und werden daher vernachlässigt.
Die Größen
$q_{ij} = \nu_i\cdot p_{ij} \qquad i,j \in \{0,1,\ldots I\}; i \neq j$
bezeichnet man als (infinitesimale) Übergangsraten (oder auch Intensitäten) der Markov-Kette $X(t)$. Da $\nu_i$ die Rate ist, mit der Zustand $i$ verlassen wird, und $p_{ij}$ die Wahrscheinlichkeit, mit der dann in den Zustand $j$ übergegangen wird, ist $q_{ij}$ die Rate, mit der der Prozeß, falls er im Zustand $i$ ist, in den Zustand $j$ übergeht.
Wegen
$\nu _i = \sum_{j \neq i} \nu_i \cdot p_{ij}= \sum_{j \neq i} q_{ij}$
und
$p_{ij}=\frac{q_{ij} }{ \nu_i } = \frac{ q_{ij} }{ \sum_{j \neq i} q_{ij} }$
kann die Markov-Kette auch durch die Übergangsraten beschrieben werden.
Diese Größen sind keine Wahrscheinlichkeiten sondern Raten. Ist $h$ allerdings sehr klein, dann können die Produkte $q_{ij} \cdot h$ als Approximationen der Wahrscheinlichkeiten für den Übergang vom Zustand $i$ zum Zustand $j$ in der infinitesimal kleinen Zeitspanne $h$ aufgefaßt werden.
In praktischen Anwendungen bestimmt man die Übergangsraten $q_{ij}$ i.d.R. direkt durch Analyse des betrachteten Systems. Man kann auch schreiben:
$P\{X (t, t + h) = j\, |\, X(t) = i\} =
q_{ij} \cdot h + o(h) $, wenn $j\neq i$
$P\{X (t, t + h) = j\, |\, X(t) = i\} =
1- \nu_i \cdot h + o(h)$, wenn $j=i$
Die Analyse eine konkreten 2-Stationen-Systems kann also auf der Grundlage der Übergangsraten $q_{ij}$ erfolgen.
Im vorliegenden Anwendungsfall beträgt für die Puffergröße $c=0$ die Übergangsrate zwischen den Zuständen $i=0$ und $j=1$: $q_{01} = \lambda$.
Denn
$P\{X (t, t + h) = 1\,|\, X(t) = 0\}
= P\{$Bearbeitungsende an Station 1 in $ h\} + o(h)$
$\quad= \lambda \cdot h + o(h)$
für $h\rightarrow 0$.
Dagegen ist die Übergangsrate zwischen den Zuständen $i=1$ und $j=2$: $q_{12} = \lambda$.
Denn
$P\{X (t, t + h) = 2\,|\, X(t) = 1\} $
$\quad = (P\{$Bearbeitungsende an Station 1 in $ h\}) \cdot (P\{$ kein Bearbeitungsende an Station 2 in $ h\} )$
$\quad= \lambda \cdot h \cdot (1-\mu \cdot h) + o(h) $
für $h\rightarrow 0$.
Die folgende Matrix gibt die Übergangswahrscheinlichkeiten zwischen den Zustanden im (sehr kleinen) Zeitraum $h$ für das betrachtete 2-Station-System für $c=0$ an. Die folgenden Berechnungen greifen auf diese Matrix zurück.
nach |
|||
von |
0 |
1 |
2 |
0 |
$(1-\lambda\cdot h)$: kein Bearbeitungsende an Station 1 |
$\lambda\cdot h$: Bearbeitungsende an Station 1 |
-- |
1 |
$(1-\lambda\cdot h)\cdot \mu\cdot h$: kein Bearbeitungsende an Station 1, Bearbeitungsende an Station 2 |
$(1-\lambda\cdot h)\cdot (1-\mu\cdot h)$: kein Bearbeitungsende an Station 1, kein Bearbeitungsende an Station 2 |
$\lambda\cdot h \cdot (1-\mu\cdot h)$: Bearbeitungsende an Station 1, kein Bearbeitungsende an Station 2 |
2 |
-- |
$\mu\cdot h$: Bearbeitungsende an Station 2 |
$(1-\mu\cdot h)$: kein Bearbeitungsende an Station 2 |
Für $c=2$ Pufferplätze ergibt sich folgende Matrix der Wahrscheinlichkeiten der Zustandsänderungen.
nach |
|||||
| von | 0 | 1 | 2 | 3 | 4 |
0 |
$(1-\lambda\cdot h)$ | $\lambda\cdot h$ | |||
1 |
$(1-\lambda\cdot h)\cdot \mu\cdot h$ | $(1-\lambda\cdot h)\cdot (1-\mu\cdot h)$ | $\lambda\cdot h \cdot (1-\mu\cdot h)$ | ||
2 |
$(1-\lambda\cdot h)\cdot \mu\cdot h$ |
$(1-\lambda\cdot h)\cdot (1-\mu\cdot h)$ | $\lambda\cdot h \cdot (1-\mu\cdot h)$ | ||
3 |
$(1-\lambda\cdot h)\cdot \mu\cdot h$ |
$(1-\lambda\cdot h)\cdot (1-\mu\cdot h)$ | $\lambda\cdot h \cdot (1-\mu\cdot h)$ | ||
4 |
$\mu\cdot h$ |
$(1-\mu\cdot h)$ | |||
Zur Bestimmung der Zustandswahrscheinlichkeiten zum Zeitpunkt $t+h$, $P_j(t+h)$, gewichtet man die Wahrscheinlichkeiten aller Zustände zum Zeitpunkt $t$, $P_i(t)$, die zum Zustand $P_j(t+h)$ im Zeitpunkt $t+h$ führen können, mit den jeweiligen Übergangswahrscheinlichkeiten $q_{ij}\cdot h$ und bildet die Summe. Bei $n$ möglichen Zuständen erhält man dann $n$ Gleichungen der folgenden Form:
$P_j(t+h) = q_{1j}·h·P_1(t) + q_{2j}·h·P_2(t) + \ldots + q_{nj}·h·P_n(t)$
Für den Fall $c=0$ erhält man z.B.:
$ P_0(t+h) = (1-\lambda\cdot h)\cdot P_0(t) + (1-\lambda\cdot h)\cdot \mu\cdot h\cdot P_1(t) $ (I)
$ P_1(t+h) = \lambda\cdot h\cdot P_0(t) + (1-\lambda\cdot h)\cdot (1-\mu\cdot h) \cdot P_1(t) + \mu \cdot h \cdot P_2$
$ P_2(t+h) = \lambda\cdot h\cdot (1-\mu\cdot h) \cdot P_1(t) + (1-\mu \cdot h) \cdot P_2$
Die weiteren Berechnungen werden anhand Gleichung (I) demonstriert.
Ausmultiplizieren
$ P_0(t+h) = P_0(t) - \lambda\cdot h \cdot P_0(t) + \mu\cdot h\cdot P_1(t) - \lambda\cdot h \cdot \mu \cdot h\cdot P_1(t) $ (Ia)
Umformen und Vernachlässigung aller $h^2$-Terme:
$ P_0(t+h) - P_0(t) = - \lambda\cdot h \cdot P_0(t) + \mu\cdot h\cdot P_1(t) $ (Ib)
Division durch $h$:
$ \frac{P_0(t+h) - P_0(t)}{h} = - \lambda \cdot P_0(t) + \mu\cdot P_1(t) $ (Ic)
Die stationären Zustandswahrscheinlichkeiten $P_j$ erhält man durch Betrachtung des Grenzübergangs $h\rightarrow 0$ und $t\rightarrow \infty$. Für $t\rightarrow \infty$ strebt dieser Differenzenquotient gegen Null (Siehe hierzu Papadopoulos/Heavey/Browne 1993, S. 55f.). Damit entsteht folgendes Gleichungssystem für die stationären Zustandswahrscheinlichkeiten, $P_{j}, (j= 0,1,2)$:
$-\lambda \cdot P_{0} + \mu \cdot P_{1} =0$
$\lambda \cdot P_{0}-(\lambda +\mu )\cdot P_{1}+\mu \cdot P_{2}=0$
$\lambda \cdot P_{1}-\mu \cdot P_{2}=0 $
oder
$\lambda \cdot P_{0}=\mu \cdot P_{1}\qquad $(a)
$(\lambda +\mu )\cdot P_{1}=\lambda \cdot P_{0}+\mu \cdot P_{2}\qquad$ (b)
$\mu \cdot P_{2}=\lambda \cdot P_{1}\qquad$ (c)
Aus (a) folgt
$P_{1}=\frac{\lambda}{ \mu }\cdot P_{0}\qquad $(d)
Aus (b) folgt
$P_{2}=\frac{\lambda}{ \mu }\cdot P_{1}+P_{1}-\frac{\lambda}{ \mu }\cdot P_{0}$
$P_{2}=\left( {\frac{\lambda }{ \mu }} \right)^2\cdot P_{0}+\frac{\lambda }{ \mu }\cdot P_{0}-\frac{\lambda }{ \mu }\cdot P_{0}$
$P_{2}=\left( {\frac{\lambda }{ \mu }} \right)^2\cdot P_{0} \qquad $(e)
Berücksichtigen wir nun, daß die Summe aller Wahrscheinlichkeiten 1 betragen muß:
$P_{0}+P_{1}+P_{2}=1 \qquad $(f)
Wir erhalten dann durch einsetzen von (d) und (e) in (f)
$P_{0}+\frac{\lambda}{ \mu }\cdot P_{0}+\left( {\frac{\lambda }{ \mu }} \right)^2\cdot P_{0}=1$
Daraus folgt
$P_{0}=\frac{1}{1+\frac{\lambda }{ \mu }+\left( {\frac{\lambda}{ \mu }} \right)^2}\qquad$(g)
Im Nenner von (g) steht eine geometrische Reihe, deren Elemente sich durch einen konstanten Faktor $\frac{\lambda}{\mu}$ unterscheiden: $({\frac{\lambda}{\mu}})^0, ({\frac{\lambda}{\mu}})^1, ({\frac{\lambda}{\mu}})^2$. Die Summe einer geometischen Reihe mit $n+1$ Gliedern, $s_n=a_0+a_1+...+a_n=a\cdot (1+q^1+q^2+...+q^n)$ beträgt $s_n=a\cdot \frac {1-q^{n+1}}{1-q}$.
Im vorliegenden Fall ergibt sich wegen $n=2$ und $a=1$:
$P_{0}=\frac{1}{\frac{ 1-\left( {\frac{\lambda }{ \mu }} \right)^3}{ 1-\frac{\lambda }{ \mu}$
oder
$P_{0}=\frac { 1-\frac{\lambda}{ \mu }}{1-\left( {\frac{\lambda }{ \mu }} \right)^3}$
Allgemein gilt bei $N+1=c+3$ Zuständen:
$\lambda \cdot P_{0}=\mu \cdot P_{1}\quad$
$(\lambda +\mu )\cdot P_{n}=\lambda \cdot P_{n-1}+\mu \cdot P_{n+1}\quad 1\leq n\leq N\quad$
$\mu \cdot P_{N}=\lambda \cdot P_{N-1}\quad$
Für $P_0$ ergibt sich dann
$P_0=\frac{1-(\frac{\lambda}{\mu})}{1-(\frac{\lambda}{\mu})^{N+1}}$
oder
$P_0=\frac{1-\rho}{1-\rho^{N+1}}$
Dieses Ergebnis ist identisch mit $P_0$ für ein $(M/M/1):(GD/N/\infty)$-Warteschlangensystem, wenn man die Produktionsrate der ersten Station als Ankunftsrate $\lambda$ und die Produktionsrate der zweiten Station als Bedienrate $\mu$ interpretiert. Das sieht dann so aus:
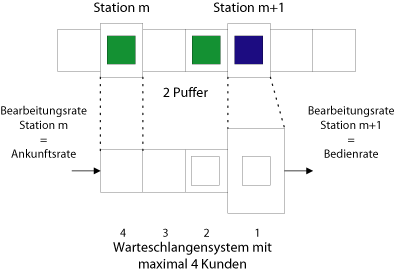
Die gesuchte Produktionsrate kann mit Hilfe von $P_0$ wie folgt ermittelt werden:
$X=(1-P_0) \cdot \mu$
Modul 2-Stationen-Flie▀produktionssystem mit exponentialverteilten Bearbeitungszeiten im Produktions-Management-Trainer:
Modul 3-Stationen-Flie▀produktionssystem mit exponentialverteilten Bearbeitungszeiten im Produktions-Management-Trainer:
Siehe auch ...
- Produktions-Management-Trainer
- Leistungsanalyse eines Fließproduktionssystems
- Fließproduktionssysteme mit unbegrenzten Puffern
- Analyse längerer Fließproduktionssysteme mit begrenzten Puffern
Literatur
| Tijms, H.C. (1994). Stochastic Models - An Algorithmic Approach. Chichester: Wiley. |