Analyse längerer Fließproduktionssysteme mit begrenzten Puffern
Während 2-Stationen-Systeme und 3-Stationen-Systeme - unter bestimmten Verteilungsannahmen - noch exakt analysiert werden können, ist dies für längere Fließproduktionssysteme nicht mehr möglich. Für diesen Fall gibt es verschiedene Approximationsverfahren, die auf dem von Gershwin vorgeschlagenen Dekompositionsansatz aufbauen. Danach wird das gesamte System in Subsysteme zerlegt, die jeweils aus zwei Stationen bestehen. Diese Subsysteme werden analysiert und die Ergebnisse werden iterativ zwischen den Subsystemen ausgetauscht.
Bei unbeschränkten Puffern konnte die Produktionsrate des Fließproduktionssystems aus der Leistungsfähigkeit des Engpasses abgeleitet werden. Der Engpaß konnte einfach als Station mit der längsten mittleren Bearbeitungszeit identifiziert werden. Wenn Blockierungen an den Stationen auftreten können, dann heißt dies, daß die prinzipiell produktiv nutzbare Zeit einer Station nicht nur aus den Phasen "beschäftigt" (arbeitet) und "unbeschäftigt" (starved) besteht. Vielmehr kommt nun noch hinzu, daß die Station "blockiert" (blocked) sein kann. Bei Störungen kommt auch noch der Zustand "gestört" hinzu.
Die beiden Zustände "beschäftigt" und "blockiert" kann man als
die Zustände zusammenfassen, in denen ein neu an einer Station
ankommendes bzw. an der Vorgängerstation fertiggestelltes
Werkstück zunächst warten muß, bis mit seiner Bearbeitung
begonnen wird.
Im folgenden wird das Dekompositionskonzept zur Analyse eines Fließproduktionssystems eingesetzt. Dabei gelten folgende Annahmen:
- asynchroner Materialfluß
- an allen Stationen exponentialverteilte Bearbeitungszeiten
- keine Störungen
- begrenzte Puffer zwischen den Stationen
- ein unbegrenzter Puffer vor Station 1 (d.h. Station ist niemals leer)
- ein unbegrenzter Puffer hinter der letzten Station $M$ (d.h. die letzte Station ist niemals blockiert)
Insbesondere die Annahme exponentialverteilter Bearbeitungszeiten ist in der Praxis selten erfüllt. Wir benutzen sie hier, weil man für diesen Fall die Berechnungen sehr schön nachvollziehen kann.
Für die Praxis bieten sich vor allem Verfahren an, die auch für allgemein-verteilte Bearbeitungszeiten bzw. deterministische Taktzeiten und Störungen geeignet sind. Derartige, ebenfalls auf dem Dekompositionskonzept basierende Verfahren sind in der Software POM Flowline Optimiser implementiert und werden in der Praxis erfolgreich eingesetzt.
Wir betrachten folgendes System mit fünf Stationen:
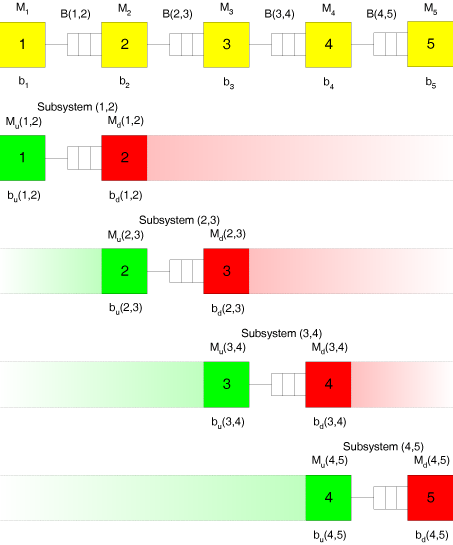
Damit die Subsysteme leicht identifiziert werden können, werden jeweils die Originalnummern der beiden in dem Subsystem enthaltenen Stationen in Klammern angegeben. $b_m$ ist die mittlere Bearbeitungszeit an Station $m$ (später wird mit der Bearbeitungsrate $\mu_m=\frac{1}{b_m}$) gerechnet. $M_u$ steht für Upstream-Station. $M_d$ steht für Downstream-Station. $b_u(m,m+1)$ ist die modifizierte Bearbeitszeit der Upstream-Station des Subsystems, das aus den Stationen $m$ und $m+1$ besteht. $b_d(m,m+1)$ ist die modifizierte Bearbeitszeit der Downstream-Station des Subsystems, das aus den Stationen $m$ und $m+1$ besteht.
Jedes Subsystem (bestehend aus den Stationen $m$ und $m+1$) hat eine Upstream-Station $M_u(m,m+1)$ (niemals leer) und eine Downstream-Station $M_d(m,m+1)$ (niemals blocked). Zwischen diesen beiden Stationen liegt der Puffer mit der Kapazität $c_{m,m+1}$.
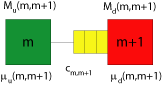
Betrachten wir einmal den Puffer zwischen den Stationen 2 und 3.
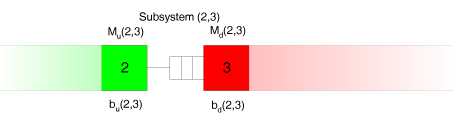
Wir stellen uns nun einen Beobachter vor, der den Zufluß von Werkstücken in den Puffer in diesem Subsystem beobachtet.
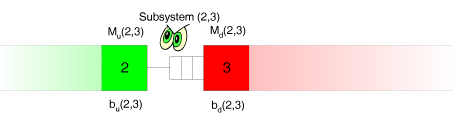
Der Beobachter sieht den Zugang von Werkstücken in den Puffer. Die Zugangsgeschwindigkeit hängt davon ab, wie schnell die stromaufwärts gelegene Station 2 arbeitet und ob sie immer über ein zu bearbeitendes Werkstück verfügt bzw. in welchem Ausmaß sie unter Materialmangel leidet. Dieser mögliche Materialmangel wird durch die Station 1 verursacht, welche der Beobachter aber nicht sehen kann.
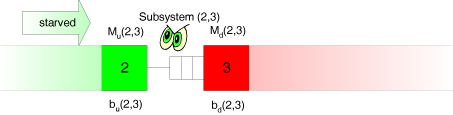
Jetzt betrachtet der Beobachter den Abfluß von Werkstücken aus dem Puffer.
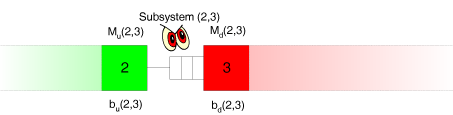
Der Abfluß von Werkstücken wird durch die Produktionsgeschwindigkeit der stromabwärts gelegenen Station 3 beeinflußt und durch das Ausmaß, in dem diese Station unter Blockierung leidet.
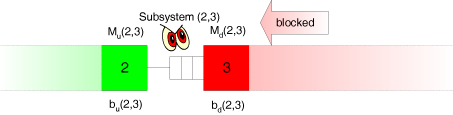
Das Ausmaß der Blockierung der Station 3 wird durch die Stationen im Fließproduktionssystem verursacht, die stromabwärts hinter der Station 3 liegen. Diese Stationen kann der Beobachter aber ebenfalls nicht sehen.
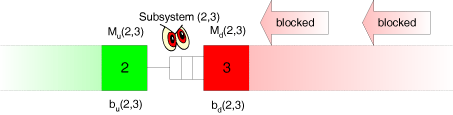
Der Beobachter kann nur den unmittelbaren Zu- und Abfluß in den Puffer direkt sehen. Die Starving- und Blockierzeiten der Stationen müssen geschätzt werden. Dies geschieht wie folgt. Wir bezeichnen mit
- $\mu_u =\frac {1}{b_u}$ die modifizierte Bearbeitungsrate der Upstream-Station
- $\mu_d = \frac {1}{b_d}$ die modifizierte Bearbeitungsrate der Downstream-Station
Die Rate $\mu_u$
soll neben der Bearbeitung an der Upstream-Station den Einfluß aller stromaufwärts gelegenen Stationen auf den Zufluß in den Puffer erfassen (Leerzeiten, starving). Die Rate $\mu_d$
soll neben der Bearbeitung an der Downstream-Station den Einfluß aller stromabwärts gelegenen Stationen auf den Abfluß aus dem Puffer wiedergegeben (Blockierzeiten, blocking).
Wir nehmen vorläufig einmal an, daß wir die modifizierte Bearbeitungsraten $\mu_d(m,m+1)$ für alle Downstream-Stationen bereits kennen. Diese $\mu_d$-Werte
berücksichtigen nicht die Starving-Effekte, wohl aber (wenn sie richtig geschätzt wurden) die
Blocking-Effekte. Wir werden diese Größen später aktualisieren. Jetzt nehmen wir einfach einmal an,
wir würden sie kennen. Als Startwert verwendet man üblicherweise $\mu_d(m,m+1)=\mu_{m+1}$
($m+1=2,\ldots,M$). Das ist natürlich eine Überschätzung der tatsächlichen Produktionsrate, da durch das Blocking Produktionsrate verlorengeht.
Berechnung der $\mu_u-$Werte:
Die $\mu_u$-Werte sind die Bearbeitungsraten der Upstream-Stationen. Sie sollen den Einfluß des gesamten vor der Upstream-Station gelegenen Segments des Fließproduktionssystems erfassen. Dies sind die Starving-Effekte, da von den Upstream-Stationen lediglich Materialmangel verursacht werden kann.
Da die erste Station des Fließproduktionssystems niemals unter Materialmangel leiden kann, gilt
$\frac{1}{\mu _u\left( {1,2} \right)}=\frac{1} {\mu _1}$
Für alle anderen Stationen $(2,3,\ldots,M)$ werden folgende Überlegungen angestellt, wobei zur Veranschaulichung das folgende Bild dient.
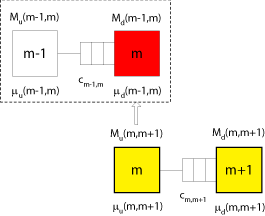
Nehmen wir einmal an, wir hätten das Subsystem ($m-1,m$) bereits analysiert. Wir kennen also bereits die Größe $\mu _u\left( {m-1,m} \right)$.
Setzen wir annahmegemß auch $\mu _d\left( {m-1,m} \right)$ als bekannt voraus, dann können wir
auch die Produktionsrate $X(m-1,m)$ des vorgelagerten Subsystems $(m-1,m)$ berechnen. Die Berechnung der Produktionsrate eines 2-Stationen-Subsystems wird hier im Detail beschrieben.
Die gesuchte Bearbeitungsrate $\mu _u(m,m+1)$ der Upstream-Station des Subsystems $(m,m+1)$ soll den Einfluß des gesamten vor dieser Station liegenden Fließproduktionssystem-Segments erfassen. Sie ergibt sich als ursprüngliche Bearbeitungszeit zuzüglich eines noch unbekannten Leerzeitzuschlags. Da die Upstream-Station eines Subsystems aber annahmegemäß nicht leer sein kann, greift man auf die Tatsache zurück, daß die Stationen $M_u(m,m+1)$ und $M_d(m-1,m)$ identisch sind, weil sie dieselbe physische Station $m$ des Originalsystems bezeichnen.
Nehmen wir nun also an, wir hätten die Produktionsrate des Subsystems $(m-1,m)$, $X(m-1,m)$ bereits geschätzt. Diese Produktionsrate ist geringer als die isolierte Bearbeitungsrate $\mu_m$ der Station $m$, da hierbei sowohl Leerzeiten als auch Blockierzeiten berücksichtigt werden. Die Produktionsrate $X(m-1,m)$ ist nun die Rate, mit der Werkstücke durch das Subsystem $(m-1,m)$ hindurchgeschleust werden. Aus dieser Produktionsrate kann man auch die durchschnittliche Zwischenabgangszeit von Werkstücken $\frac{1}{X(m-1,m)}$ ermitteln. Wäre die Downstream-Station niemals leer, dann könnte sie mit der Rate $\mu_d(m-1,m)$ arbeiten und die Zwischenabgangszeit wäre $\frac{1}{\mu_d(m-1,m)}$.
Wenn nun die Downstream-Station im Subsystem $(m-1,m)$ schneller arbeitet kann als das Subsystem $(m-1,m)$, dann muß sie hin und wieder warten. Die Wartezeit ist damit die Differenz aus $\frac{1}{\mu_m}$ und$\frac{1}{X(m-1,m)}$. Damit können wir $\mu_u(m,m+1)$ aus $X(m-1,m)$ und $\mu_d(m-1,m)$ ableiten:
$\frac{1}{\mu _u\left( {m,m+1} \right)} =\frac{1}{\mu _m}+ \underbrace{\left[ {\frac{1}{X\left( {m-1,m} \right)}- \frac{1}{\mu _d\left( {m-1,m} \right)}} \right]}_{\mathrm{= mittlere Leerzeit}} \qquad m=2,3,...,m-1 $
Zur Bestimmung der Produktionsrate $X(m-1,m)$ wird das hier beschriebene Verfahren eingesetzt.
Berechnung der $\mu_d-$Werte:
Die $\mu_d$-Werte sind die Bearbeitungsraten der Downstream-Stationen. Sie sollen den Einfluß des gesamten hinter der Downsstream-Station gelegenen Segments des Fließproduktionssystems erfassen. Dies sind die Blocking-Effekte, da von den Downstream-Stationen lediglich Blockierungen verursacht werden können.
Da die letzte Station des gesamten Fließproduktionssystems niemals blockiert sein kann, gilt:
$\frac{1}{\mu _d\left( {M-1,M} \right)}=\frac{1} {\mu _M}$
Für alle anderen Stationen gilt folgendes, wobei das folgende Bild zur Veranschaulichung dient.
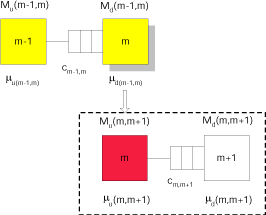
Die Argumentation ist ähnlich wie bei der Quantifizierung der Leerzeiten.
Die Bearbeitungrate $\mu_d(m-1,m)$ der Downstream-Station $m$ eines Subsystems soll den Einfluß des hinter dieser Station liegenden Fließproduktions-Segments erfassen.Sie ergibt sich als ursprüngliche Bearbeitungszeit zuzüglich eines noch unbekannten Blockierzeitzuschlags. Da die Downstream-Station eines 2-Stations-Systems aber annahmegemäß nicht blockiert sein kann, greift man auf die Tatsache zurück, daß die Stationen $M_d(m-1,m)$ und $M_u(m,m+1)$ identisch sind, weil sie dieselbe Station $m$ des Originalsystems bezeichnen.
Nehmen wir nun wieder an, wir hätten die Produktionsrate des Subsystems $(m,m+1)$ bereits ermittelt. Außerdem nehmen wir an, daß wir die modifizierte Bearbeitungsrate der Upstream-Station $M_u(m,m+1)$ dieses Subsystems kennen. Deren Berechnung haben wir ja bereits oben beschrieben. In diesem Fall können wir die mittlere Blockierzeit der Upstream-Station $M_u(m,m+1)$ als Differenz zwischen dem Kehrwert der Produktionsrate $X(m,m+1)$ und dem Kehrwert der modifizierten Bearbeitungsrate der Upstream-Station $M_u(m,m+1)$, $\mu_u(m,m+1)$, ermitteln. Da in $\mu_u(m,m+1)$ die Blockierungseffekte noch nicht enthalten sind, sondern nur die Starving-Effekte, ist $\mu_u(m,m+1)$ größer als $X(m,m+1)$. Die Differenz der Kehrwerte ergibt die mittlere Blockierdauer:
$\frac{1}{\mu _d\left( {m-1,m} \right)} =\frac{1}{\mu _m}+ \underbrace{\left[ {\frac{1}{X\left( {m,m+1} \right)}- \frac{1}{\mu _u\left( {m,m+1} \right)}} \right]}_{\mathrm{mittlere Blockierzeit}} \qquad m=M-1,M-2,...,2$
Zur Lösung des Gleichungssystems geht man zusammenfassend wie folgt vor. Man
nimmt zunächst an, daß die $\mu_d$-Werte bekannt seien. Das
entspricht der Vorstellung, daß der Abgangsprozeß aller Stationen
aktiv ist. Man legt $\mu_u(1,2)$ fest und
bestimmt dann in einer Vorwärtsrechnung nacheinander alle
$\mu_u(m,m+1)$-Werte. Dann geht man von den zuvor berechneten
$\mu_u$-Werten aus und bestimmt in einer Rückwärtsrechnung nacheinander alle $\mu_d$-Werte. Diese beiden Rechenschritte
wiederholt man so lange, bis eine stabile Lösung gefunden wurde.
Modul M/M/1-Modelle (begrenzte Puffer, Dekomposition) im Produktions-Management-Trainer:
Siehe auch ...
- Produktions-Management-Trainer
- Leistungsanalyse eines Fließproduktionssystems
- Fließproduktionssysteme mit unbegrenzten Puffern
- Analyse eines 2-Stationen-Systems mit begrenztem Puffer
Literatur
| Günther, H.-O. und Tempelmeier, H. (2020). Supply Chain Analytics - Operations Management und Logistik. 13. Aufl., Norderstedt: Books on Demand. |
| Tempelmeier, H. (2020), Production ANalytics. 6. Aufl., Norderstedt: Books on Demand. | Tempelmeier, H. (2020). Analytics in Supply Chain Management und Produktion - Übungen und Mini-Fallstudien. 7. Aufl., Norderstedt: Books on Demand. |