CONWIP-System
Das CONWIP-System (CONstant Work-In-Process) implementiert wie das Kanban-System das Pull-Prinzip. Im Unterschied zum Kanban-System, in dem für jede Produktart ein eigener Kartenkreislauf eingerichtet wird, wird im CONWIP-System ein Kartentyp für mehrere Produkte verwendet. Außerdem umfassen die Regelkreise, in denen die Produktions-Autorisierungskarten zirkulieren, mehrere aufeinanderfolgende Stationen des Fließproduktionssystems. Nach Abschluß der Bearbeitung eines Werkstücks an der letzten Station wird das Werkstück in das Fertigproduktlager gelegt. Die CONWIP-Karte haftet weiter an dem Werkstück.
Nach Eintreffen eines Kundenauftrags wird das betreffende Fertigprodukt aus dem Lager entnommen und die CONWIP-Karte an den Systemanfang geschickt. Dort wartet sie, bis sie an die Reihe kommt. Nachdem die Station 1 ein Werkstück bearbeitet hat und folglich wieder frei geworden ist, wird über die Festlegung der nächsten Produktart entschieden. Für diese Entscheidung benötigt man ein Kriterium, nach dem die freien CONWIP-Karten den Produktarten zugeordnet werden. Man kann z.B. für jedes Produkt die kumulierte Plan-Produktionsmenge mit der kumulierten Ist-Produktionsmenge vergleichen und dann das Produkt mit der größten Differenz auswählen.
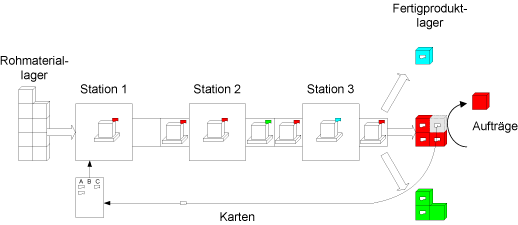
Der Vorteil des CONWIP-Systems gegenüber dem liegt darin, daß keine produktspezifischen Zwischenlagerbestände geführt werden müssen.
Unter bestimmten Annahmen kann man ein CONWIP-System als ein geschlossenes Warteschlangennetzwerk (Produktform-Netzwerk) modellieren. Dies soll im Folgenden gezeigt werden, wobei von folgenden Annahmen ausgegangen wird:
- das Fließproduktionssystem besteht aus $M$ Stationen
- alle Produkte werden zu einem repräsentativen Produkt aggregiert
- die Bearbeitungszeit an der Station $m$ ist mit dem Mittelwert $b_m$ exponentialverteilt
- es zirkulieren $N$ CONWIP-Karten
- die Puffer vor den Stationen sind unbegrenzt
- das Rohmateriallager ist niemals leer
- die Nachfrage nach den Produkten ist unbegrenzt, d.h. unmittelbar nach der Fertigstellung eines Produkts an Station $M$ wird die CONWIP-Karte zurück an den Systemanfang geschickt
Das folgende Bild zeigt die Struktur dieses CONWIP-Systems. Wegen der Annahme unbegrenzter Nachfrage kann das Fertigproduktlager aus der Betrachtung ausgeschlossen werden. Wenn nach der Fertigstellung eines Produkts an Station 3 die CONWIP-Karte sofort einem neuen Produkt bzw. Rohmaterial zugeordnet und dieses in die Warteschlange vor Station 1 eingeordnet wird, dann ist der Lagerbestand, d.h. die Anzahl Werkstücke, in dem Fließproduktionssystem (work-in-process, WIP) immer konstant gleich der Anzahl CONWIP-Karten. Die grauen CONWIP-Karten in der Plantafel entsprechen den beiden produktspezifischen CONWIP-Karten in der Warteschlange vor Station 1. Durch die Plantafel wird angedeutet, daß die Warteschlange bis zum Beginn der nächsten Bearbeitung an Station 1 noch umsortiert werden kann.
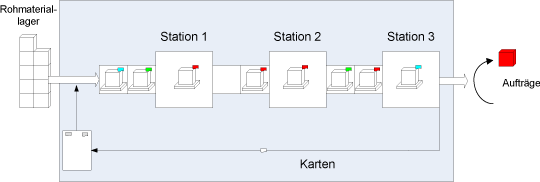
In diesem Fall kann die Produktionsrate des Fließproduktionssystems als Funktion der Anzahl CONWIP-Karten u.a. mit der Mittelwertanalyse (mean-value analysis, MVA) exakt berechnet werden. Dabei werden folgende Überlegungen angestellt:
a) mittlere Durchlaufzeit eines Werkstücks an Station $m$
Nehmen wir an, ein Werkstück trifft an der Station $m$ ein und wird sich dort in wenigen Augenblicken am Ende der Warteschlange einreihen (FCFS-Warteschlangendisziplin). Im Zeitpunkt unmittelbar vor dem Eintreffen des Werkstücks befinden sich an der Station $A_m(N)$ Werkstücke. Die Zeitspanne, die vergeht, bis das betrachtete Werkstück die Station nach der Bearbeitung wieder verläßt, ist dann gleich der Bearbeitungszeit des Werkstücks plus der Zeitspanne, welche die Station zur Abarbeitung der anderen Werkstücke benötigt, die sich bereits zum Zeitpunkt der Ankunft des Werkstücks in der Station befinden. Die mittlere Durchlaufzeit $D_m(N)$ eines Werkstücks an Station $m$ kann dann durch folgende Beziehung dargestellt werden.
$D_m(N) =b_m\cdot A_m(N)+b_m \qquad m=1,2,\ldots,M$
Dabei bezeichnet $A_m(N)$ die mittlere Anzahl der Werkstücke, die sich zum Ankunftszeitpunkt (arrival-instant) an der Station $m$ befinden. Zwischen der "arrival-instant"-bezogenen und der "time-average"-bezogenen Anzahl von Werkstücken $Q_m(N)$ an Station $m$ besteht unter den getroffenen Annahmen folgende wichtige Beziehung:
$A_m(N) = Q_m(N-1) \qquad m=1,2,\ldots,M$
b) mittlere Produktionsrate der Station $m$
Eine u.a. für die Berechnung der Produktionsrate wichtige Beziehung wird durch das Gesetz von Little beschrieben. Es besagt im betrachteten Kontext, daß die Anzahl von Werkstücke im System, $N$, gleich dem Produkt aus der mittleren Produktionsrate $X$ und der Durchlaufzeit $D$ ist. Für ein Fließproduktionssystem mit nur einem Produkttyp wird dieser Zusammenhang mit der folgenden Gleichung beschrieben:
$L=\lambda \cdot W\qquad $ (Anzahl Werkstücke im System = Produktionsrate $\cdot$ Durchlaufzeit)
oder
$N=X(N)\cdot D(N)$
oder
$X(N)=\frac{N}{D(N)$
Da die Anzahl CONWIP-Karten $N$ eine bekannte Größe ist, müssen wir nur noch $D(N)$, die mittlere Durchlaufzeit (die von der Anzahl CONWIP-Karten abhängt) durch das gesamte Fließproduktionssystem, ermitteln. Die mittlere Durchlaufzeit ergibt sich aus der Summe der stationsbezogenen Durchlaufzeiten:
$D(N)= \displaystyle{\sum_{m=1}^M} D_m(N)$
Setzen wir nun $D(N)$ in Little's Formel ein, dann erhalten wir
$X(N)= \frac{N}{\displaystyle{\sum_{m=1}^M} D_m(N)}$
Um stationsbezogene Durchlaufzeiten $D_m(N)$ berechnen zu können, müssen wir aber die Größen $A_m(N)$ kennen. Um $A_m(N)$ zu ermitteln, benötigen wir $Q_m(N-1)$. Um $Q_m(N-1)$ zur bestimmen, wenden wir Little’s Gesetz auf eine Station an, d.h.
$Q_m(N) = X_m(N) \cdot D_m(N) \qquad m=1,2,...,M$
Damit können wir nun folgendes Verfahren zur Bestimmung der Produktionsrate eines geschlossenen Fließproduktionssystems mit $N$ zirkulierenden CONWIP-Karten und exponentialverteilten Bearbeitungszeiten an den Stationen beschreiben:
| $Q_m(0)=0$ | $m=1,2,...,M$ | |
| For $n=1,...,N$ | ||
| $A_m(n)=Q_m(n-1)$ | $m=1,2,...,M$ | |
| $D_m(n)=[1+A_m(n)]\cdot b_m$ | $m=1,2,...,M$ | |
| $X(n)=\frac{n}{\displaystyle{\sum_{m=1}^m} D_m(n)}$ | ||
| $X_m(n)=X(n)$ | $m=1,2,...,M$ | |
| $Q_m(n)=X_m(n)\cdot D_m(n)$ | $m=1,2,...,M$ | |
| endfor | ||
Beispiel: Wir betrachten ein CONWIP-System mit 8 Stationen, einem (aggregierten) Produkt, exponentialverteilten Bearbeitungszeiten $b_m=1 (m=1,2,\ldots,8)$ und 7 CONWIP-Karten. Für dieses System erhält man folgende Zwischenergebnisse:
| $n$ | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Durchlaufzeit $D_m(n)$ | |||||||
| $m=$1 | 1 |
1.125 |
1.25 |
1.375 |
1.5 |
1.625 |
1.75 |
| $m=$2 | 1 |
1.125 |
1.25 |
1.375 |
1.5 |
1.625 |
1.75 |
| $m=$3 | 1 |
1.125 |
1.25 |
1.375 |
1.5 |
1.625 |
1.75 |
| $m=$4 | 1 |
1.125 |
1.25 |
1.375 |
1.5 |
1.625 |
1.75 |
| $m=$5 | 1 |
1.125 |
1.25 |
1.375 |
1.5 |
1.625 |
1.75 |
| $m=$6 | 1 |
1.125 |
1.25 |
1.375 |
1.5 |
1.625 |
1.75 |
| $m=$7 | 1 |
1.125 |
1.25 |
1.375 |
1.5 |
1.625 |
1.75 |
| $m=$8 | 1 |
1.125 |
1.25 |
1.375 |
1.5 |
1.625 |
1.75 |
| $\sum D_m(n)$ | 8 |
9 |
10 |
11 |
12 |
13 |
14 |
| Produktionsrate $X(n)$ | 0.125 |
0.2222 |
0.3 |
0.3636 |
0.4167 |
0.4615 |
0.5 |
| Lagerbestand $Q_m(n)$ | |||||||
| $m=$1 | 0.125 |
0.25 |
0.375 |
0.5 |
0.625 |
0.75 |
0.875 |
| $m=$2 | 0.125 |
0.25 |
0.375 |
0.5 |
0.625 |
0.75 |
0.875 |
| $m=$3 | 0.125 |
0.25 |
0.375 |
0.5 |
0.625 |
0.75 |
0.875 |
| $m=$4 | 0.125 |
0.25 |
0.375 |
0.5 |
0.625 |
0.75 |
0.875 |
| $m=$5 | 0.125 |
0.25 |
0.375 |
0.5 |
0.625 |
0.75 |
0.875 |
| $m=$6 | 0.125 |
0.25 |
0.375 |
0.5 |
0.625 |
0.75 |
0.875 |
| $m=$7 | 0.125 |
0.25 |
0.375 |
0.5 |
0.625 |
0.75 |
0.875 |
| $m=$8 | 0.125 |
0.25 |
0.375 |
0.5 |
0.625 |
0.75 |
0.875 |
Man erkennt, daß bei 7 CONWIP-Karten die Produktionsrate erst 50% des theoretischen Maximalwertes beträgt. Die folgende Graphik zeigt, daß die Produktionsrate durch die weitere Erhöhung der Anzahl CONWIP-Karten noch beträchtlich gesteigert werden kann. Da $n$ der Bestand im System ist, zeigt die Graphik anschaulich den Konflikt zwischen Produktivität und Bestand. Will man den Bestand senken, dann geht das bei niedrigen Werten von $n$ nur, wenn man Produktivitätsverluste in Kauf nimmt.
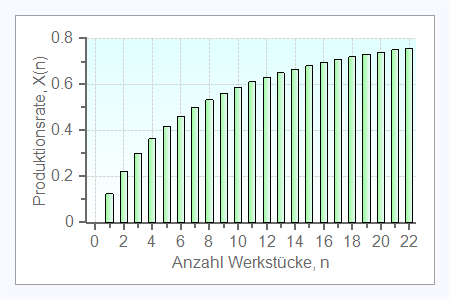
Erweiterungen:
- Falls die CONWIP-Karten erst dann von den Fertigprodukten getrennt und an den Systemanfang geschickt werden, wenn ein Kundenauftrag zu einer Lagerentnahme geführt hat, dann muß der Bestand im Fertigproduktlager mit in die Betrachtung einbezogen werden. Für ein solches Systems führt man eine Synchronisierungsstation ein, die die Wartezeit eines Fertigprodukts auf einen Kundenauftrag abbildet. Man kann dann auch Lagerservicegrade berechnen.
- Weiterhin wird man die Betrachtung auf mehrere Produktarten ausweiten müssen.
- Schließlich gibt es CONWIP-gesteuerte Fließproduktionssysteme, in denen die Puffer zwischen den Stationen begrenzt sind.
Für die genannten Erweiterungen gibt es spezielle Analyseverfahren, die allerdings wesentlich komplexer sind als der oben gezeigte einfache Algorithmus zur Bestimmung der Produktionsrate der Fließproduktionssystems als Funktion der Anzahl CONWIP-Karten.
Siehe auch ...
- Produktions-Management-Trainer, Modul CONWIP-System
- Kanban-System
Literatur
| Tempelmeier, H. (2020). Production Analytics. 6. Aufl., Norderstedt: Books on Demand. |
| Günther, H.-O. und Tempelmeier, H. (2020). Supply Chain Analytics - Operations Management und Logistik. 13. Aufl., Norderstedt: Books on Demand. |
