Einflußgrößen der Leistung von Fließproduktionssystemen unter stochastischen Bedingungen
Im folgenden werden Fließproduktionssystemen (FPS) unter stochastischen Bedingungen betrachtet. In diesem Fall sind die Zeitspannen, während deren sich die Werkstücke an den Stationen aufhalten, mehr oder weniger großen zufälligen Schwankungen unterworfen. Diese Schwankungen zwingen i.a. dazu, die einzelnen Stationen zu entkoppeln, z.B. durch Einfügen von Puffern.
In der Praxis werden stochastische Einflüsse bei der Fließbandabstimmung oft durch den sog. Bandwirkungsfaktor berücksichtigt, durch den die Taktzeit bei der Zuordnung der Arbeitselemente zu den Stationen künstlich verkürzt wird. Ein Problem dabei ist allerdings, daß niemand den Bandwirkungsfaktor kennt. Denn dessen Höhe hängt von der Konfiguration des Fließproduktionssystems, insbesondere auch von den Puffergrößen ab.
Betrachtet man ein in der Praxis laufendes FPS, dann wird man feststellen, daß die Aufenthaltsdauer eines Werkstücks an einer Station nicht mehr exakt vorhersehbar, sondern stochastisch ist. Warum ist das so?
Hierfür gibt es mehrere Ursachen:
Schwankungen der Bearbeitungszeiten
Wenn die Stationen nun Handarbeitsplätze sind,
dann treten durch den Menschen verursachte Schwankungen der Bearbeitungszeiten auf. Selbst bei Produktion nur einer Produktart und bei perfekter
Fließbandabstimmung (balanced flow line), wenn also die Mittelwerte der Bearbeitungszeiten an
allen Stationen identisch sind, können die Bearbeitungszeiten der einzelnen Werkstücke
individuell variieren. Dies wird in der deterministischen Fließbandabstimmung nicht berücksichtigt.
Empirischen Untersuchungen zufolge sind Bearbeitungszeiten bei manuellen Tätigkeiten linkssteil verteilt mit Variationskoeffizienten im Bereich von $CV=0.1$
bis $CV=0.6$. Der Variationskoeffizient wird i.a. als ein Maß für die Streuung der
Bearbeitungszeiten verwendet. Er ist bekanntlich als Quotient aus Standardabweichung und Mittelwert wie folgt definiert:
$CV=\frac{\sigma}{\mu}$
In analytischen Modellen wird oft auf theoretische Verteilungen zurückgegriffen.
- Exponentialverteilung
In analytischen Modellen, die auf Methoden der Warteschlangentheorie zurückgreifen, greift man häufig auf die Exponentialverteilung zurück. Die Exponentialverteilung hat folgende Dichtefunktion:
$f(x)=\lambda \cdot e^{-\lambda \cdot x} \qquad x \geq 0$
Graphisch sieht die Dichtefunktion der Exponentialverteilung wie folgt aus:
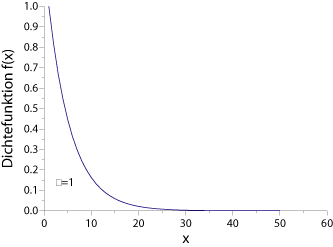
Die Momente der Exponentialverteilung lauten:
$E\{X\} = \frac{1}{\lambda}$ (Erwartungswert)
$V\{X\} = \frac{1}{\lambda^2}$ (Varianz)
Der Variationskoeffizient beträgt folglich:
$CV\{X\} = \frac{ \sqrt{V\{X\}} }{ E\{X\} } = \frac{1}{\lambda}\cdot
\frac{\lambda}{1}=1 $
- Gamma-Verteilung
Eine sehr flexible Wahrscheinlichkeitsverteilung zur Beschreibung der Bearbeitungszeiten ist die Gamma-Verteilung. Dies ist eine Verteilung mit zwei Parametern, einem Lageparameter $\alpha$ und einem Streuungsparameter $k$.
Die Dichtefunktion lautet:
$f(x) = \frac{{\alpha ^k x^{k - 1} e^{ - \alpha x} }}{{\Gamma \left( k \right)}},\qquad x \geq 0$
Die Momente der Gamma-Verteilung lauten:
$E\left\{ X \right\} = \frac{k}{\alpha }$ (Erwartungswert)
$V\left\{ X \right\} = \frac{k}{{\alpha ^2 }}$ (Varianz)
Daraus folgt:
$k=\frac{E\left\{ X \right\}^2}{V\left\{ X \right\}}$
$\alpha=\frac{E\left\{ X \right\}}{V\left\{ X \right\}}$
Das folgende Bild zeigt verschiedene Gamma-Verteilungen mit demselben Mittelwert und unterschiedlichen Varianzen bzw. Variationskoeffizienten.
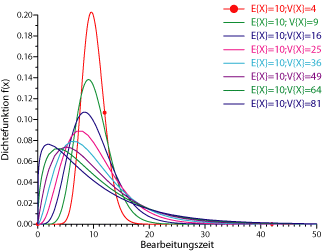
Wie man sieht, ist die Gamma-Verteilung eine sehr flexible zweiparametrige Verteilung, mit der man unterschiedliche Verteilungsformen approximieren kann.
Die minimale Bearbeitungszeit eines Werkstücks an einer Station kann in der Praxis oft weniger als 50 % der normalen, d.h. durchschnittlichen Bearbeitungszeit betragen. Einige Unternehmen gehen auch davon aus, daß der Schwankungsbereich der Bearbeitungszeit an einem Handarbeitsplatz zwischen 80 % und 150 % des Mittelwerts liegt.
Oft sind nicht nur die Bearbeitungszeiten der einzelnen Werkstücke an einer Station unterschiedlich, sondern auch die mittleren Bearbeitungszeiten aller Werkstücke an den Stationen. Wenn z.B. die Fließbandabstimmung (Arbeitsverteilung) nicht perfekt gelungen ist, dann haben die Stationen unterschiedliche Arbeitsbelastungen (Stationszeiten) zu bewältigen. Dies kann bedeuten, daß z.B. Station 3 eine mittlere Belastung von 33 Sekunden hat, während die Nachfolgestation 4 nur durchschnittlich 27 Sekunden beschäftigt ist. Diese Ungleichverteilung der Arbeitslast kann das Ergebnis der deterministischen Fließbandabstimmung für ein System mit einem Produkt sein, wenn die Zuordnung der Arbeitselemente nicht anders möglich ist. Aber auch dann, wenn keine Fließbandabstimmung erfolgt ist, kann es aus technischen Gründen oft zu unausgeglichenen Belastungen kommen. Dies ist dann der Fall, wenn man für jedes Arbeitselement eine Station einrichtet und die Elementzeiten und damit auch die Stationszeiten unterschiedlich sind.
Solche Fließproduktionssysteme nennt man unbalancierte Systeme. Diese Unterschiede der mittleren Stationszeiten werden i.d.R. noch überlagert durch die stochastischen Schwankungen der Bearbeitungszeiten der einzelnen Werkstücke.
Mehrere Produktarten (Produktmix)
Wenn mehrere Produktarten in wahlfreier Reihenfolge in das Fließproduktionssystem eingeschleust werden, können die Aufenthaltsdauern der Werkstücke aus der Sicht einer Station ebenfalls schwanken - selbst bei deterministischen Bearbeitungszeiten. Da die einzelnen Werkstücke unterschiedliche Bearbeitungszeiten haben, kann man die Bearbeitungszeit eines beliebigen Werkstücks aus der Sicht einer Station als stochastisch betrachten. Wird bei der Einlastung der Werkstücke an der ersten Station ein vorgegebenes Mischungsverhältnis eingehalten, dann kann man die zu erwartenden mittleren Bearbeitungszeiten an den einzelnen Stationen aus den produktartspezifischen Bearbeitungszeiten ableiten.
Störungen
Es treten Störungen auf: Werkzeugbruch, Maschinenausfälle, Probleme mit der Zuführung von Material, etc. Störungen können zeitabhängig oder nutzungsabhängig sein. Nutzungsabhängige Störungen treten nur während der Bearbeitungszeiten auf (z.B. Werkzeugbruch). Zeitabhängige Störungen können immer auftreten, z.B. bei einem Antrieb einer Maschine, die sich im Leerlauf befindet. Störungen treten auch unter sonst deterministischen Bedingungen auf, z.B. bei einer perfekt ausgetakteten Transferstraße, die nur eine Produktart mit identischen Bearbeitungszeiten an allen Stationen bearbeitet.
Oft wird in analytischen Modellen angenommen, daß die Abstände zwischen Ausfällen einer Exponentialverteilung folgen (d.h. $CV=1.0$). Auch die Weibullverteilung oder die Erlang-Verteilung werden oft angenommen.
Man muß i.a. eine theoretische Verteilung annehmen, da der Fabrikplaner i.d.R. nur sehr wenig Informationen über die Störungscharakteristika hat. Maschinenhersteller geben oft nur die mittlere störungsfreie Laufzeit (mean time to failure, MTTF) an. Die Reparaturzeiten erhöhen die Zeitspanne, während der eine Station durch ein Werkstück belegt ist. Man nimmt oft an, daß die Reparaturzeiten aufgrund der verschiedenen unterschiedlichen Defekte, die aufgetreten sein können, wesentlich höhere Variationskoeffizienten haben ($CV>1.0$). In vielen Fällen wird aber für die Reparaturzeiten eine Exponentialverteilung angenommen. Erlang-2-verteilte Stördauern werden z.T. in der Automobilindustrie unterstellt.
In der Praxis verwendet man zur Beschreibung der Zuverlässigkeit einer Station die Kennziffer Verfügbarkeit. Diese ist definiert als
$V=\frac{\mathrm{MTTF}}{\mathrm{MTTF}+\mathrm{MTTR}}$
und beschreibt das Verhältnis der störungsfreien Laufzeit zur Gesamtzeit. MTTR (mean time to repair) ist mittlere Stördauer. Diese besteht aus der technisch bedingten Reparaturzeit und einer Wartezeit auf den Mitarbeiter, der die Reparatur ausführt. Die Wartezeit wird durch die Struktur des Instandhaltungssystems beeinflußt (z.B. Anzahl Mitarbeiter; zentral, dezentral, Patrouille oder nicht, etc.).
Zur Veranschaulichung des Einflusses der Störungen auf die Produktionsrate eines FPS betrachten wir ein System mit zehn identischen vollautomatisierten Stationen. Die Bearbeitungszeiten bzw. Taktzeiten seien deterministisch und an allen Stationen einheitlich gleich eins. Die Stationen unterliegen operationsabhängigen Störungen und die Puffer sind beschränkt. Die Störungen treten mit exponentialverteilten Abständen mit dem Mittelwert MTTF auf und die Reparaturdauer ist ebenfalls eine exponentialverteilte Zufallsvariable mit dem Mittelwert MTTR. Das folgende Bild zeigt für unterschiedliche Verfügbarkeiten, welchen Einfluß die mittlere Reparaturdauer (MTTR) bei variierenden Puffergrößen auf die Produktionsrate hat.
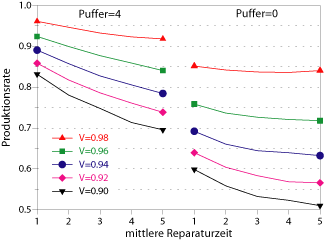
Offensichtlich reicht es nicht aus, zur
Beschreibung der Leistungsfähigkeit einer Station neben der
Stationszeit die Verfügbarkeit anzugeben, wie dies in der Praxis
häufig geschieht. Es kann durchaus vorkommen, daß ein System mit
niedrigen Verfügbarkeiten der Stationen bei einer kurzen mittleren
Reparaturzeit eine höhere Produktionsrate hat als ein System mit
höheren Verfügbarkeiten, dessen mittlere Reparaturzeit relativ
lang ist. Die Ursache liegt darin, daß sich Störungen bei kurzen
Reparaturzeiten relativ leicht durch Pufferbestände kompensieren lassen. Insofern kann ein System mit vielen kurzen Störungen eine
höhere Produktionsrate aufweisen als in System mit wenigen langen
Störungen und derselben mittleren Verfügbarkeit.
Produktionsfehler
Eine weitere Ursache für Schwanlungen der Aufenthaltsdauern der Werkstücke an den Stationen besteht darin, daß Ausschuß an den Stationen entstehen kann. Ein Werkstück muß evtl. an der Station sofort wieder aufgearbeitet werden. Dann erhöht sich die Arbeitslast der Station. Alternativ kann das Werkstück aus dem Produktionssystem ausgeschleust werden. Dann resultiert aus diesem Werkstück überhaupt kein Zeitbedarf an der nächsten und allen nachfolgenden Stationen. Allerdings benötigt man dann separate Reparaturkapazitäten.
Die genannten stochastischen Einflüsse führen dazu, daß die Aufenthaltsdauern der Werkstücke an den Stationen nicht mehr - wie bei der deterministischen Leistungsabstimmung unterstellt wird - perfekt aufeinander abgestimmt sind. Eine Station wartet daher zeitweise auf Nachschub von der Vorgängerstation (starving) oder sie kann ein bearbeitetes Werkstück aufgrund von Platzmangel nicht sofort an die Nachfolgerstation weitergegeben (blocking). In beiden Fällen kommt es zu einem Produktionsverlust, dessen Ausmaß nicht primär von den Leistungsmerkmalen einer einzelnen Station, sondern von dem Zusammenwirken aller Stationen beeinflußt wird.
In all diesen Fällen kann man die Produktionsmenge des Fließproduktionssystems nicht mehr so einfach vorhersagen, wie das unter deterministischen Bedingungen möglich ist. Denn durch die nicht mehr exakt aufeinander abstimmbaren Bearbeitungszeiten der einzelnen Werkstücke treten nun verschiedene Effekte auf:
- Blockierung (blocking)
Blockierung tritt auf, wenn eine Station zwar mit ihrer Arbeit fertig ist, wenn sie aber das Werkstück nicht weitergeben kann,
weil an der nachfolgenden Station noch kein Platz für das Werkstück ist. Wenn gleichzeitig vor der Station wieder ein
unbearbeitetes Werkstück wartet, dann ist die Station blockiert.
- Leerzeiten (starving)
Leerzeit (starving) tritt auf, wenn eine Station unbeschäftigt ist, weil kein unbearbeitetes Werkstück verfügbar ist.
Beide Formen der Nicht-Ausnutzung der verfügbaren Kapazität sollte man so weit wie möglich reduzieren, wenn man Produkte herstellen kann, die man auf dem Markt auch verkaufen kann. Insbesondere in der Konfigurierungsphase eines Fließproduktionssystems spielt die Nicht-Ausnutzung der Ressourcen eine bedeutende Rolle. Denn wenn man durch Verringerung der Nicht-Ausnutzung die Menge der benötigten Ressourcen (Stationen) verringern kann, dann ist das natürlich ein ökonomischer Vorteil.
Prinzipiell gilt: ein schlecht konfiguriertes Fließproduktionssystem mit hohem Anteil an blocking und starving benötigt tendenziell mehr Ressourcen als ein gut
konfiguriertes Fließproduktionssystem, das dieselbe
Produktionsmenge herstellen kann.
Um ein Fließproduktionssystem
optimal, ohne Verschwendung ("lean") konfigurieren zu können, muß man aber in der Lage sein, die interessierenden
Kenngrößen (Produktionsmenge, Blockierungsanteile,
Leerzeitanteile) der verschiedenen Konfigurationsalternativen ex
ante zu bestimmen.
Genau dies ist mit analytischen Methoden zur Leistungsanalyse möglich, die im Softwaresystem POM FlowEval implementiert sind.
Siehe auch ...
- Produktions-Management-Trainer
- Leistungsanalyse von Fließproduktionssystemen
- Fließproduktionssysteme mit unbegrenzten Puffern
- Analyse von 2-Stationen-Systemen mit begrenztem Puffer
- Analyse längerer Fließproduktionssysteme mit begrenzten Puffern
Literatur
| Günther, H.-O. und Tempelmeier, H. (2020). Supply Chain Analytics - Operations Management und Logistik. 13. Aufl., Norderstedt: Books on Demand. |
| Tempelmeier, H. (2020), Production ANalytics. 6. Aufl., Norderstedt: Books on Demand. | Tempelmeier, H. (2020). Analytics in Supply Chain Management und Produktion - Übungen und Mini-Fallstudien. 7. Aufl., Norderstedt: Books on Demand. |