(r,S)-Politik
Bei Verfolgung einer $(r,S)$-Lagerhaltungspolitik wird nach folgender Entscheidungsregel vorgegangen:
In Abständen von r Perioden wird eine Lagerbestellung in der Höhe ausgelöst, die – falls sie sofort eintreffen würde – den Lagerbestand auf das Niveau S anheben würde.
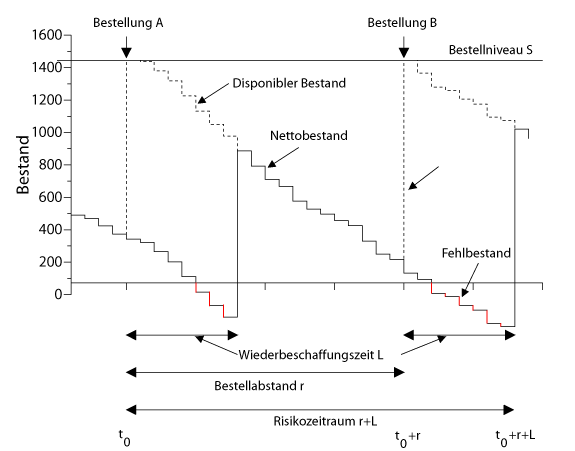
Das obige Bild zeigt die Entwicklung des Lagerbestands bei Anwendung einer $(r,S)$-Lagerhaltungspolitik. Wir gehen im folgenden davon aus, daß der Bestellabstand ()Überwachungszyklus $r$ extern vorgegeben ist. Er kann z.B. durch die Beziehung
$r_{{opt}}=\frac{q_{{opt}}}{E\left\{ D \right\}}= \frac{{optimale\;\; Bestellmenge}}{{mittlere\;\; Periodennachfragemenge}}$
festgelegt worden sein. In diesem Fall dient das Bestellniveau zur Absorption
der Unsicherheit bezüglich der Nachfragemenge in der Wiederbeschaffungszeit.
Betrachten wir einmal das oboge Bild genauer. Hier sind zwei aufeinanderfolgende
Bestellungen dargestellt. Bestellung $A$ wird in $\tau=t_0$ ausgelöst und trifft in
$(t_0+L)$ im Lager ein. Bestellung $B$ wird in $\tau=t_0+r$ ausgelöst und trifft in
$(t_0+r+L)$ im Lager ein. Bestellungen können nur in den diskreten Zeitpunkten
$\tau=t_0$, $t_0+r$, $t_0+2\cdot r$, usw.\ ausgelöst werden.
Damit das Auftreten von Lieferunfähigkeit (Fehlmengen) möglichst vermieden wird, muß die Bestellung im Zeitpunkt $\tau=t_0$ mindestens so groß sein, daß sie den Bedarf bis zum Zeitpunkt $(t_0+r+L)$ abdeckt. Denn die nächste -- in $\tau=t_0+r$ aufgegebene -- Bestellung $B$ trifft frühestens im Zeitpunkt $(t_0+r+L)$ im Lager ein.
Lieferunfähigkeit des Lagers tritt möglicherweise kurz vor dem Zeitpunkt $(t_0+r+L)$ ein, und zwar dann, wenn die Nachfragemenge im Intervall $[t_0,t_0+r+L]$ das Bestellniveau $S$, d.\,h.\ den im Zeitpunkt $t_0$ disponiblen Lagerbestand,übersteigt.
Die Höhe des Bestellniveaus wird so bestimmt, daß ein angestrebter Servicegrad im Risikozeitraum erreicht wird. Nimmt man an, daß die Nachfrage stationär ist, d.h. wenn die Charakteristik der Nachfrage sich im betrachteten Zeitraum nicht verändert, dann bleibt das Bestellniveau konstant.
Verläuft die Nachfrage zwar stochastisch, aber nicht-stationär, dann muß der Wert des Bestellniveaus von Zeit zu Zeit angepaßt werden. Dies führt zu Schwankungen der tatsächlichen Bestellmengen, da nicht nur die seit der letzten Bestellung beobachteten Nachfragemengen, sondern auch die Änderungen des Sicherheitsbestands in die Bestellung mit einfließen. Dies ist eine der Ursachen für den Bullwhip-Effekt, der beim Lieferanten entsteht.
Die $(r,S)$-Lagerpolitik läßt sich mit geringerem Überwachungsaufwand anwenden als die $(s,q)$-Lagerpolitik. Ein besonderer Vorteil ist darin zu sehen, daß die Beschaffungstermine mehrerer unabhängiger Produkte, die von demselben Lieferanten bezogen werden, aufeinander abgestimmt werden können. Dies erlaubt die Nutzung kostengünstigerer Transportmittel als bei produktindividueller Beschaffung. Werden die Produkte eigenproduziert, dann kann man z.B. Produktionstermine für Produkte mit einem gemeinsamen Rüstvorgang bei Einsatz der $(r,S)$-Politik aufeinander abstimmen.
Ein Nachteil sind die von der aktuellen Entwicklung der Nachfrage abhängigen Schwankungen der Bestellmengen, da diese in der Praxis oft durch bestimmte Restriktionen nicht frei variiert werden können. Ist der Beschaffungspreis z.B. aufgrund von Mengenrabatten abhängig von der Bestellmenge, dann kann es sinnvoll sein, die Bestellmenge extern vorzugeben, anstatt sie in Abhängigkeit von der aktuellen Lagerbestandsentwicklung zu bestimmen. Darüber hinaus birgt der längere Risikozeitraum der $(r,S)$-Politik ($r+L$ anstatt $L$) die Gefahr einer größeren Streuung der lagerbedingten Lieferzeiten der Kundenaufträge in sich. Dieses aus der Sicht eines Kunden äußerst wichtige Leistungskriterium eines Lagers wird allerdings in der Literatur trotz seiner hohen Praxisrelevanz nur sehr selten in die Optimierungsüberlegungen einbezogen.
Siehe auch ...
- Produktions-Management-Trainer, Modul (r,S)-Politik
- (r,s,q)-Politik
- (s,S)-Politik
- (r,S)-Politik
- Mehrstufige Lagerpolitiken
Literatur
| Tempelmeier, H. (2020). Analytics im Bestandsmanagement. 7. Aufl., Norderstedt: Books on Demand. |
| Günther, H.-O. und Tempelmeier, H. (2020). Supply Chain Analytics - Operations Management und Logistik. 13. Aufl., Norderstedt: Books on Demand. |
