(s,q)-Politik
Bei Verfolgung einer (s,q)-Lagerhaltungspolitik wird nach folgender Entscheidungsregel vorgegangen:
Immer dann, wenn der (disponible) Lagerbestand auf die Höhe des Bestellpunkts $s$ gesunken ist, wird eine Bestellung der Höhe $q$ ausgelöst.
Der disponible Lagerbestand ist die Summe aus dem physischen Bestand plus den ausstehenden, noch nicht eingetroffenen Bestellungen abzüglich der aufgelaufenden Fehlmengen.
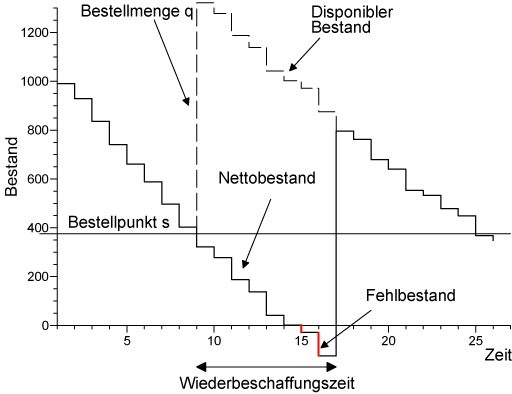
Die Entwicklung des Lagerbestands bei Anwendung eines $(s,q)$-Lagerhaltungssystems für ein Produkt zeigt das obige Bild Der durchgezogene Linienzug beschreibt den sog. Nettobestand. Ist dieser positiv, dann ist physischer Bestand vorhanden. Ist der Nettobestand negativ, dann spricht man von Fehlbestand. Der disponible Lagerbestand unterscheidet sich vom Nettobestand nur in den Perioden mit positivem Bestellbestand. In den anderen Perioden sind beide Größen identisch. Die Orientierung der Bestellentscheidung am disponiblen Bestand – und nicht am Nettobestand – bewirkt, daß in den Perioden unmittelbar nach einer Bestellung nicht erneut bestellt wird. Der disponible Bestand hat somit eine Gedächtnisfunktion. Der Vergleich des Bestellpunkts mit dem disponiblen Bestand verhindert also die mehrfache Auslösung von Bestellungen.
Achtung: Im Bild wird der Bestellpunkt s bei der Auslösung der Bestellung durch den disponiblen Lagerbestand nicht genau getroffen. Dies ist - anders als in vielen Lehrbüchern unterstellt - der Normalfall in der Realität. In der Praxis hat der disponible Bestand unmittelbar vor Auslösung der Bestellung den Bestellpunkt bereits unterschritten. Es tritt das sog. Defizit (undershoot) auf. Dies ist der Fall, wenn der Lagerbestand nur in diskreten Zeitabständen (täglich) erfaßt wird. Aber auch dann, wenn eine kontinuierliche Lagerüberwachung erfolgt, wenn aber die Auftragsgrößen größer als 1 sind, kommt es regelmäßig zu einem Defizit. Das Defizit muß man bei der Bestimmung der optimalen Höhe des Bestellpunkts mit berücksichtigen. Geschieht dies nicht, dann wird der Sicherheitsbestand falsch berechnet und der angestrebte Servicegrad wird nicht erreicht. Dieser Planungsfehler ist in der Praxis die Regel.
Ein einfaches Beispiel aus einem Lehrbuch so das verdeutlichen (Chopra/Meindl, Supply Chain Management, 5. Auflage, Hallbergmoos(Pearson) 2014, Beispiel 2.5): Die wöchentliche Nachfragemenge nach Lego-Bausteinen bei einem Einzelhändler ist mit dem Mittelwert 2500 und der Standardabweichung 500 normalverteilt. Die Wiederbeschaffungszeit beträgt 2 Wochen. Die Bestellmenge ist 10000. Der angestrebte ß-Servicegrad ist 97.5%.
Setzt man das (s,q)-Lagerhaltungsmodell unter der Annahme einer kontinuierlichen Lagerüberwachung zur Bestimmung des Bestellpunkts s ein, dann ergibt sich der Bestellpunkt s=5067 und ein Sicherheitsbestand in Höhe von 67. Wird der Lagerbestand nun aber jeweils am Periodenende überwacht, dann erreicht man anstelle des angestrebten Servicegrades von 97.5% nur 88%. Bei korrekter Modellierung des tatsächlich ablaufenden Lagerprozesses würde man einen erheblich größeren Sicherheitsbestand benötigen, und zwar 417.
Während in der Theorie oft von einer kontinuierlichen Zeitachse ausgegangen wird, wird in der Praxis mit einer diskreten Zeiteinteilung gearbeitet. Dies ist auch die Sicht der Warenwirtschaftssysteme, die die Nachfrage pro Tag erfassen und speichern. Die gesamte an einem Tag eingetroffene Nachfrage für ein Produkt wird dann als Periodennachfrage betrachtet. Der Lagerbestand wird üblicherweise am Ende eines Tages ermittelt. Dann wird auch die Entscheidung getroffen, ob eine Bestellung beim Lieferanten auszulösen ist.
Eine $(s,q)$-Politik mit diskreter Zeitachse und täglicher Bestandsüberwachung ist daher eine (r,s,q)-Lagerpolitik (mit einem Überwachungszyklus $r=1$). Prinzipiell kann man auch Überwachungszyklen, die größer als 1 sind, verwenden. In einer $(r=5,s,q)$-Lagerpolitik wird z.B. am Ende jeder Periode der Lagerbestand erfaßt (und mit dem Bestellpunkt $s$ verglichen), aber nur höchstens in Abständen von 5 Perioden bestellt. Es kann dabei vorkommen, daß der Bestellpunkt unterschritten wird, aber erst nach weiteren 4 Perioden tatsächlich bestellt wird. Diese Lagerpolitik hat einen längeren Risikozeitraum als die $(r=1,s,q)$-Lagerpolitik und führt daher auch unter sonst gleichen Bedingungen zu einem höheren Sicherheitsbestand.
Module (s,q)-Politik und Simulation einer (s,q)-Politik im Produktions-Management-Trainer:
Siehe auch ...
- Produktions-Management-Trainer, Modul (s,q)-Politik
- (r,s,q)-Politik
- (s,S)-Politik
- (r,S)-Politik
- Mehrstufige Lagerpolitiken
Literatur
| Tempelmeier, H. (2020). Analytics im Bestandsmanagement. 7. Aufl., Norderstedt: Books on Demand. |
| Günther, H.-O. und Tempelmeier, H. (2020). Supply Chain Analytics - Operations Management und Logistik. 13. Aufl., Norderstedt: Books on Demand. |