Siehe auch ...

Lineare Optimierung

Unter dem Begriff „Lineare Optimierungsprobleme“ wird eine Gruppe mathematischer Optimierungsprobleme zusammengefaßt, die folgende Eigenschaften aufweisen:

- Das Kriterium zur Auswahl der „besten“ Werte der Entscheidungsvariablen kann als lineare Funktion dieser Variablen beschrieben werden. Diese Funktion nennt man auch Zielfunktion.
- Die zu berücksichtigenden Nebenbedingungen können als eine Menge linearer Gleichungen oder Ungleichungen beschrieben werden (Proportionalität und Additivität).

LP-Modelle gehören zu den am meisten in der Praxis eingesetzten Entscheidungsmodellen. Hierfür gibt es mehrere Gründe:

- Eine Vielzahl praktischer Probleme kann zumindest angenähert durch eine Menge linearer Gleichungen und Ungleichungen beschrieben werden.
- Es gibt sehr effiziente Algorithmen zur Bestimmung der optimalen Lösung.
- Im Rahmen der Sensitivitätsanalyse kann leicht der Einfluß von Datenänderungen auf die Struktur der optimalen Lösung ermittelt werden.

Bei der Formulierung linearer Programme sind drei Schritte zu vollziehen:

Schritt 1: Identifizierung der Entscheidungsvariablen und Benennung jeder Variablen mit einem Symbol.

Schritt 2: Identifizierung der zu beachtenden Nebenbedingungen als Funktionen der Entscheidungsvariablen.

Schritt 3: Identifizierung der Zielfunktion als Funktion der Entscheidungsvariablen.

Beispiel eines LP-Modells

Mischungsproblem:

Ein Unternehmen produziert zwei Produkte A und B mit Hilfe von zwei Rohstoffen, die nur in begrenzten Mengen verfügbar sind.

  Produkt A Produkt B Verfügbar
Rohstoff 1 6 4 24
Rohstoff 2 1 2 6
Deckungsbeitrag 5 4  

Aus einer Marktanalyse weiß man, daß die maximale Nachfrage für Produkt B höchstens 2 Mengeneinheiten beträgt. Außerdem soll die Produktionsmenge für Produkt B höchstens eine Mengeneinheit mehr als die Produktionsmenge von Produkt A betragen.

Um diese Problemstellung nun in die Form eines LP-Modells zu bringen, geht man wie folgt vor.

Schritt 1:

x1 Produktionsmenge Produkt A

x2 Produktionsmenge Produkt B

Schritt 2:

Nebenbedingung I:
6 ·x1+4·x2 <= 24
Nebenbedingung II:
1 ·x1+2·x2 <= 6
Nebenbedingung III:
-1 ·x1+1·x2 <= 1
Nebenbedingung III:
1 ·x2 <= 2
Nichtnegativitätsbedingungen:
x1, x2 >= 0

Schritt 3:

Zielfunktion:
Z=5·x1+4·x2

Das LP-Modell lautet damit:

Max Z= 5·x1 +4·x2      
u.B.d.R.          
  6·x1 +4·x2 <= 24 Rohstoff 1
  1·x1 +2·x2 <= 6 Rohstoff 2
  -1·x1 +1·x2 <= 1  
    1·x2 <= 2  
  x1, x2, >= 0  

Zur Lösung eines LP kann man den Simplex-Algorithmus einsetzen. Jeder Student sollte die Rechenschritte dieses Verfahrens in einer Operations-Research-Vorlesung erlernt haben.

Zunächst muß man das obige LP-Problem zunächst in die sog. Normalform bringen, indem man die Ungleichungen durch die Einführung von Schlupfvariablen in Gleichungen überführt. Die folgenden Bildschirme sind aus dem LP-Modul (einer alten Version) des Produktions-Management-Trainers entnommen. Die "s"-Variablen sind die Schlupfvariablen. Die Ungleichheitszeichen markieren den Typ der Ungleichung in dem ursprünglichen Modell. Aufgrund der Einführung der Schlupfvariablen ist jede Zeile als Gleichung zu lesen, z.B. 6*X(1)+4*X(2)+1*s1=24.

1

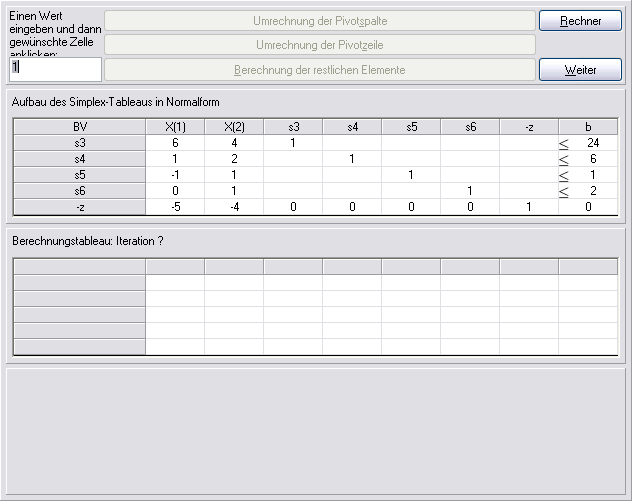
Dann werden in mehreren Iterationen einige Nicht-Basisvariablen zu Basisvariablen gemacht. Hierzu werden zunächst die Pivotzeile und die Pivotspalte bestimmt und dann der Variablentausch ausgeführt:

2

3

4

5

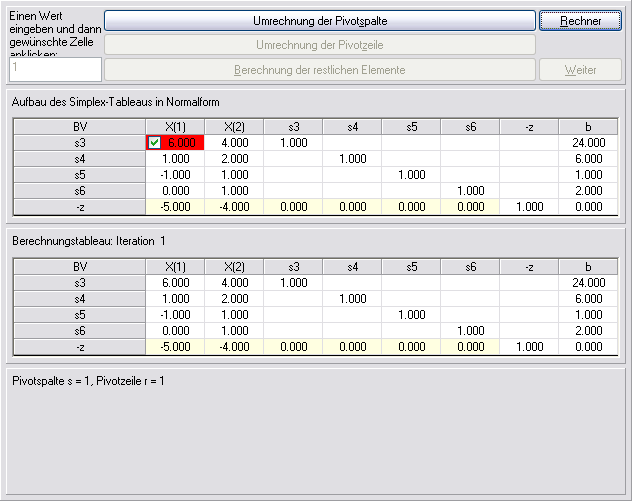
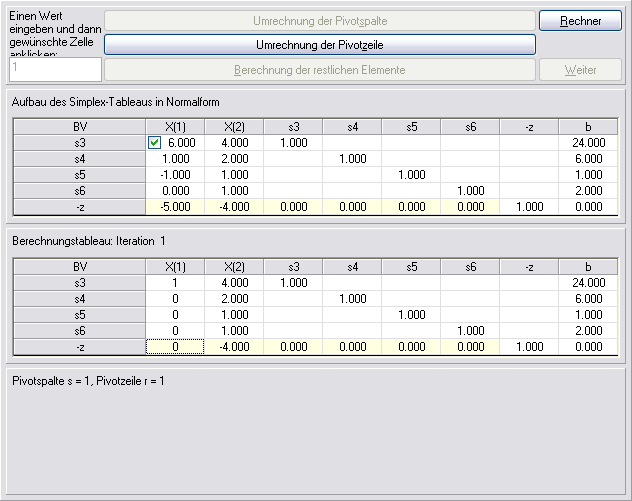
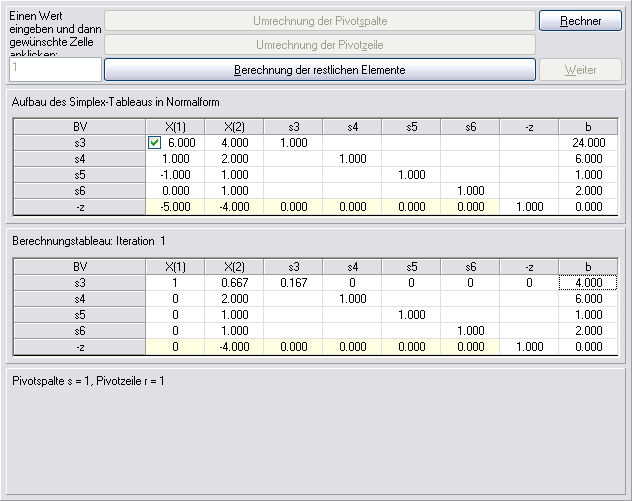
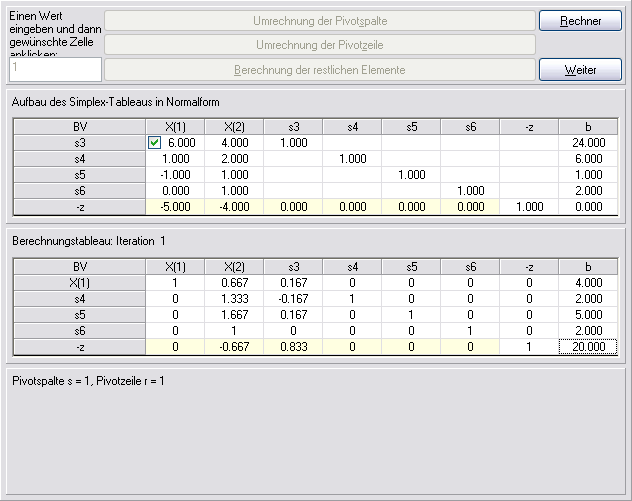
Nach der ersten Simplex-Iteration beträgt der neue Zielwert 20. Der negative Wert in der Zielfunktionszeile in Spalte X(2) zeigt uns, daß diese Lösung noch weiter verbessert werden kann. Daher wird eine weitere Simplex-Iteration durchgeführt, die zu folgender optimaler Lösung führt: X(1)=3, X(2)=1.5 und Z=21.

6

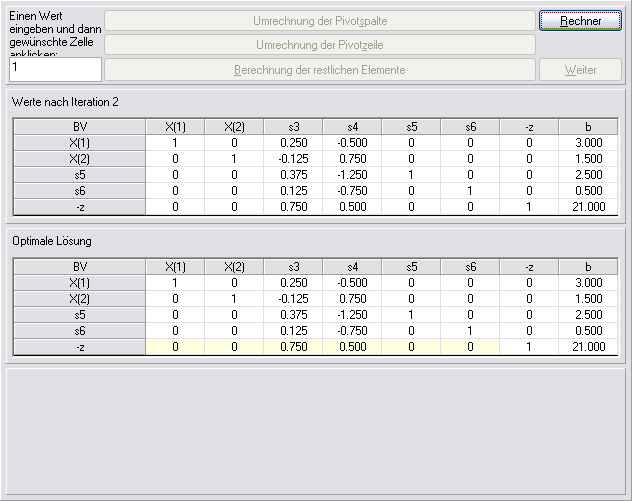
Lineare Optimierungsmodelle werden heute in fast allen Advanced-Planning-Systemen (in den Anwendungsmoduln "Master Planning", "Supply Network Planning", "Enterprise Planning") eingesetzt.

Zur Lösung praktischer Probleme greift man auf Modellgeneratoren und Standardsolver zurück. Im Beispiel sieht die Beschreibung des LP-Modells im AMPL wie folgt aus:

# Modelldefinition
set Constr;
set Var;
param Rhs {Constr};
param C {Var};
param Aij {Constr, Var};
var X {Var} >= 0;
maximize Total:
sum {j in Var} C[j] * X[j];
subject to Restrictions {i in Constr}:
sum {j in Var} Aij[i,j]*X[j] <= Rhs[i];

# Datendefinition
set Constr := M1 M2 Demand1 Demand2;
set Var := X1 X2;
param Rhs :=
M1 24
M2 6
Demand1 1
Demand2 2;
param Aij:
X1 X2 :=
M1 6 4
M2 1 2
Demand1 -1 1
Demand2 0 1;
param C := X1 5 X2 4;

Nach dem Start erscheint AMPL mit folgender Eingabeaufforderung:

ampl:

Man gibt dann die folgende AMPL-Anweisungen an:

ampl:

model PRODPLAN.mod;
ampl:
data PRODPLAN.dat;
ampl:
option solver cplex;
ampl:
solve;
ampl:
display X;

Als Ausgabe erhält man dann:

X [*] := X1 3
X2 1.5 ;