Ablaufplanung bei Reihenproduktion (Flow-Shop)
Bei Reihenproduktion sind die Ressourcen dem Arbeitsplan der Produkte entsprechend angeordnet. Alle Produkte besuchen die Ressourcen in derselben Reihenfolge. Für die Bestimmung der Einlastungsreihenfolge der Aufträge gibt es verschiedene Verfahren, deren Anwendbarkeit u.a. von der Anzahl der Produktionsstufen abhängt.
Besonders bekannt ist das exakte Verfahren von Johnson, das die zykluszeitminimale Reihenfolge für N Aufträge an 2 Maschinen bestimmt. Ein weiteres Verfahren, das dieselbe Problemstellung wie das Verfahren von Johnson, allerdings für eine beliebige Anzahl von Maschinen, heuristisch löst, die die NEH-Heuristik.
1. Flowshop mit 2 Maschinen, N Aufträge, Ziel ist die Minimierung der Zykluszeit (makespan)
-> Algorithmus von Johnson
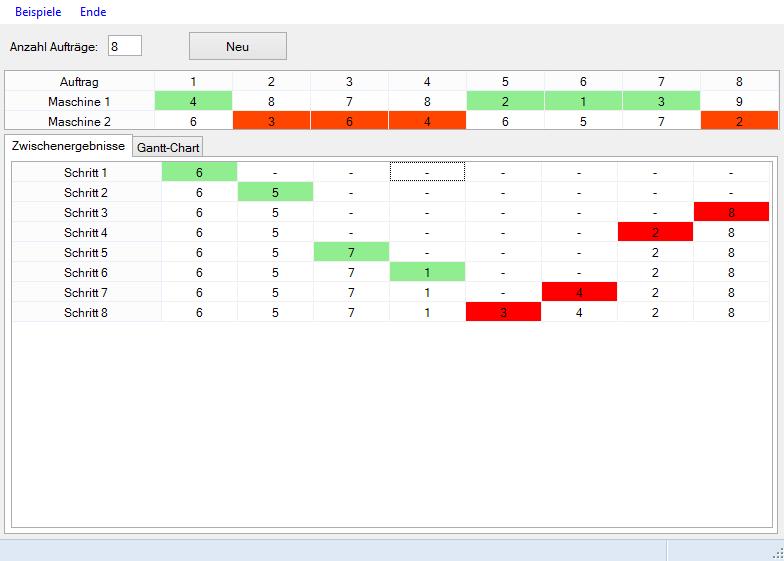
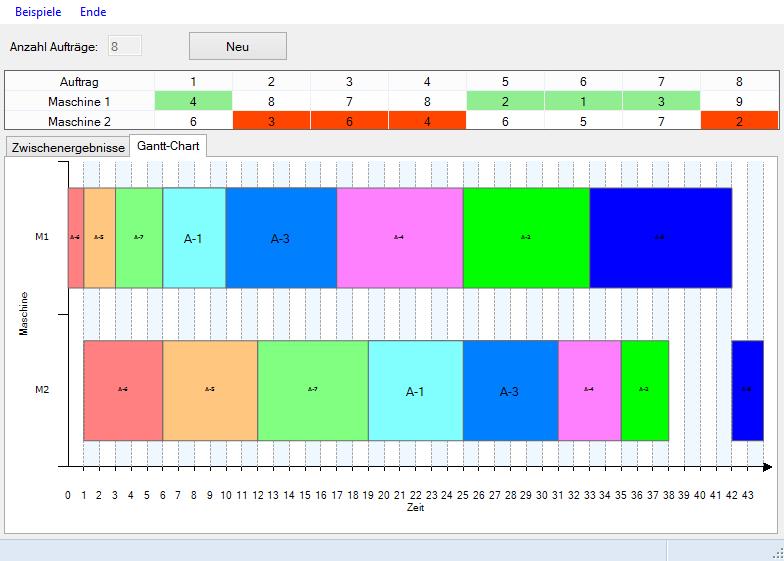
Zur Beschreibung des Verfahrens siehe Tempelmeier(2010), Aufgabe B3.6 Die folgenden mit dem Produktions-Management-Trainer erzeugten Bilder zeigen den Ablauf des Verfahrens.
2. Flowshop mit M Maschinen, N Aufträge, Ziel ist die Minimierung der Zykluszeit (makespan)
-> NEH-Heuristik
Hier wird wie folgt vorgegangen:
- Bestimme für jeden Auftrag $i$ die Summe der Bearbeitungszeiten an allen Maschinen
$T_i =\sum_{m=1}^{M} a_{im}$
und sortiere die Aufträge absteigend nach diesem Kriterium.
- Setze $\ell=2$. Nimm die Aufträge mit den Rängen $1$ und $2$ und
bestimme die Zykluszeit für die Reihenfolgen $\{1,2\}$ und $\{2,1\}$. Fixiere die (partielle) Reihenfolge mit der
geringsten Zykluszeit (makespan): $\pi^\ell=\{\pi(1),\pi(2)\}$
- Setze $\ell=\ell+1$. Nimm den nächsten Auftrag mit dem Rang $\ell$ und füge ihn der Reihe nach in jede Position der
Reihenfolge $\pi^{\ell-1}$ (im vorhergehenden Schritt ermittelt) ein. Wenn die optimale
Reihenfolge z.B. $4-3-5-2$ ist und man den Auftrag 1 einfügen will, dann erhält man:
(1-4-3-5-2), (4-1-3-5-2), (4-3-1-5-2), (4-3-5-1-2), (4-3-5-2-1)
Bestimme für jede Reihenfolge die Zykluszeit und fixiere die (partielle) Reihenfolge mit der kürzesten Zykluszeit.
- Falls $\ell=P$ (Anzahl Aufträge) STOP; andernfalls gehe zu Schritt 3.
Die Berechnung der Zykluszeit verlangt die Nachbildung des zeitlichen Produktionsablaufs und geht wie folgt, wobei die Indizes $i$
die aktuelle Reihenfolge beschreiben:
- Auftrag i kann an Maschine j erst beginnen, wenn er an Maschine j-1 beendet
wurde:
START(i,j) >= ENDE(i,j-1) alle i,j
- Maschine j kann mit Auftrag i erst beginnen, wenn der Auftrag i-1 auf dieser Stufe beendet
wurde:
START(i,j) >= ENDE(i-1,j) alle i,j
- Das Bearbeitungsende des Auftrags i auf Stufe j ergibt sich aus dem Bearbeitungsbeginn zuzüglich der Rüstzeit und der
Bearbeitungszeit:
ENDE(i,j) = START(i,j) + a(i,j) alle i,j
- F(0,j) = 0
- F(i,0) = 0
Beispiel:
Daten
Auftrag |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Maschine 1 |
4 |
1 |
5 |
2 |
5 |
1 |
3 |
3 |
2 |
4 |
Maschine 2 |
3 |
5 |
6 |
2 |
1 |
1 |
2 |
3 |
4 |
3 |
Maschine 3 |
4 |
1 |
5 |
2 |
5 |
1 |
3 |
3 |
2 |
4 |
Maschine 4 |
3 |
5 |
6 |
2 |
1 |
5 |
2 |
2 |
4 |
1 |
Vorbereitung:
Rang |
Auftrag |
$T_i$ |
1 |
3 |
22 |
2 |
1 |
14 |
3 |
2 |
12 |
4 |
5 |
12 |
5 |
9 |
12 |
6 |
10 |
12 |
7 |
8 |
11 |
8 |
7 |
10 |
9 |
4 |
8 |
10 |
6 |
8 |
$\ell=2$; Bestimmung der ersten Reihenfolge ; die Angaben in den Auftragsspalten sind die jeweiligen Endtermine ENDE(i,j) der Aufträge an den jeweiligen Machinen.
Akt. Reihenfolge |
3 |
1 |
M-1 |
5 |
9 |
M-2 |
11 |
14 |
M-3 |
16 |
20 |
M-4 |
22 |
25 |
Akt. Reihenfolge |
1 |
3 |
M-1 |
4 |
9 |
M-2 |
7 |
15 |
M-3 |
11 |
20 |
M-4 |
14 |
26 |
Optimale Reihenfolge: |
3-1 |
|
Zykluszeit: |
25 |
|
Gantt-Diagramm:
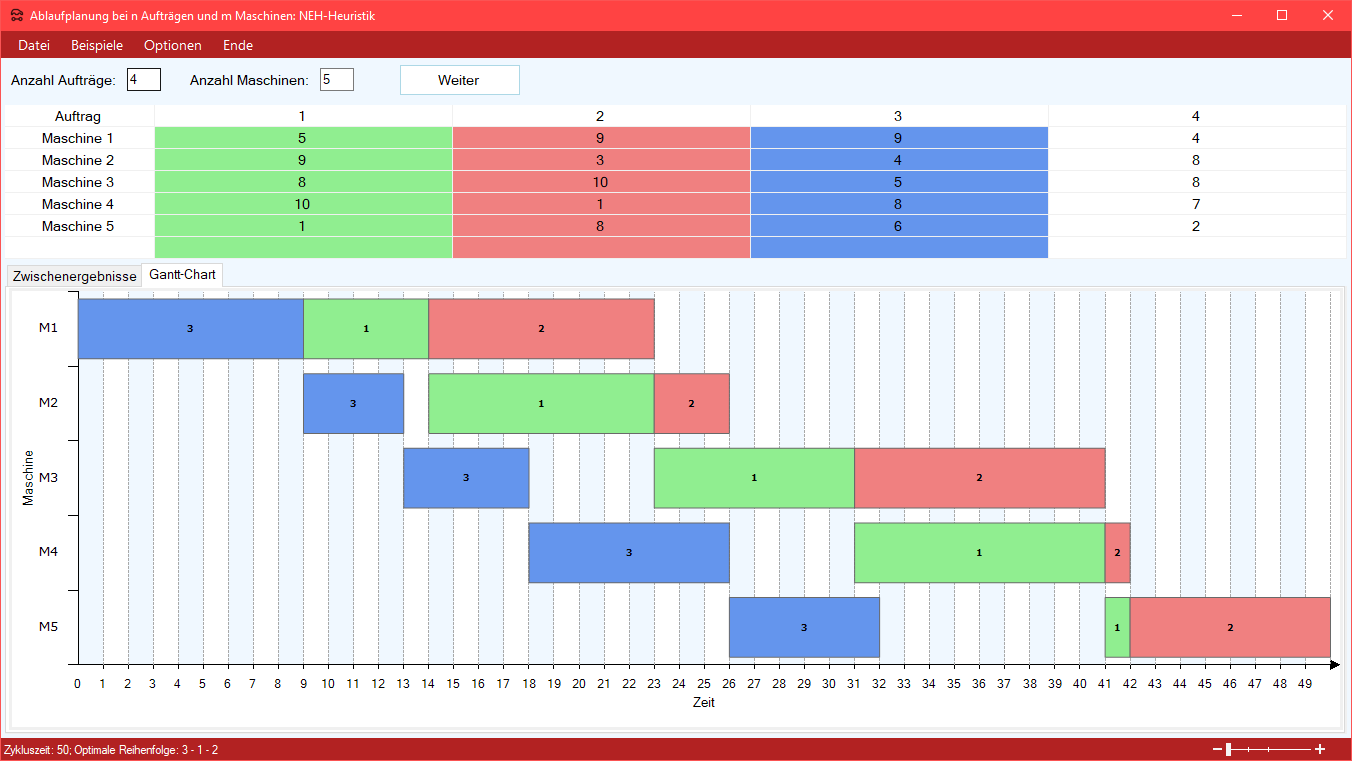
Auftrag 3 / 12 |
|
|
|
Akt. Reihenfolge |
2 |
3 |
1 |
M-1 |
1 |
6 |
10 |
M-2 |
6 |
12 |
15 |
M-3 |
7 |
17 |
21 |
M-4 |
12 |
23 |
26 |
Akt. Reihenfolge |
3 |
2 |
1 |
M-1 |
5 |
6 |
10 |
M-2 |
11 |
16 |
19 |
M-3 |
16 |
17 |
23 |
M-4 |
22 |
27 |
30 |
Akt. Reihenfolge |
3 |
1 |
2 |
M-1 |
5 |
9 |
10 |
M-2 |
11 |
14 |
19 |
M-3 |
16 |
20 |
21 |
M-4 |
22 |
25 |
30 |
Optimale Reihenfolge: |
2-3-1
|
Zykluszeit: |
26 |
|
|
Gantt-Diagramm:
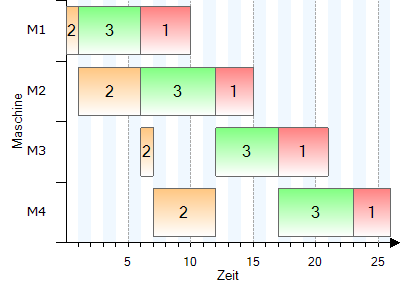
Auftrag 4 / 12 |
|
|
|
|
Akt. Reihenfolge |
5 |
2 |
3 |
1 |
M-1 |
5 |
6 |
11 |
15 |
M-2 |
6 |
11 |
17 |
20 |
M-3 |
11 |
12 |
22 |
26 |
M-4 |
12 |
17 |
28 |
31 |
Akt. Reihenfolge |
2 |
5 |
3 |
1 |
M-1 |
1 |
6 |
11 |
15 |
M-2 |
6 |
7 |
17 |
20 |
M-3 |
7 |
12 |
22 |
26 |
M-4 |
12 |
13 |
28 |
31 |
Akt. Reihenfolge |
2 |
3 |
5 |
1 |
M-1 |
1 |
6 |
11 |
15 |
M-2 |
6 |
12 |
13 |
18 |
M-3 |
7 |
17 |
22 |
26 |
M-4 |
12 |
23 |
24 |
29 |
Akt. Reihenfolge |
2 |
3 |
1 |
5 |
M-1 |
1 |
6 |
10 |
15 |
M-2 |
6 |
12 |
15 |
16 |
M-3 |
7 |
17 |
21 |
26 |
M-4 |
12 |
23 |
26 |
27 |
Optimale Reihenfolge: |
2 - 3 - 1 - 5
|
Zykluszeit: |
27 |
|
|
|
Gantt-Diagramm:
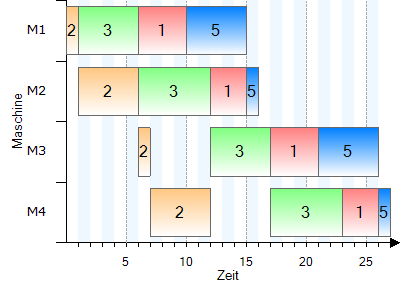
Auftrag 5 / 12 |
|
|
|
|
|
Akt. Reihenfolge |
9 |
2 |
3 |
1 |
5 |
M-1 |
2 |
3 |
8 |
12 |
17 |
M-2 |
6 |
11 |
17 |
20 |
21 |
M-3 |
8 |
12 |
22 |
26 |
31 |
M-4 |
12 |
17 |
28 |
31 |
32 |
Akt. Reihenfolge |
2 |
9 |
3 |
1 |
5 |
M-1 |
1 |
3 |
8 |
12 |
17 |
M-2 |
6 |
10 |
16 |
19 |
20 |
M-3 |
7 |
12 |
21 |
25 |
30 |
M-4 |
12 |
16 |
27 |
30 |
31 |
Akt. Reihenfolge |
2 |
3 |
9 |
1 |
5 |
M-1 |
1 |
6 |
8 |
12 |
17 |
M-2 |
6 |
12 |
16 |
19 |
20 |
M-3 |
7 |
17 |
19 |
23 |
28 |
M-4 |
12 |
23 |
27 |
30 |
31 |
Akt. Reihenfolge |
2 |
3 |
1 |
9 |
5 |
M-1 |
1 |
6 |
10 |
12 |
17 |
M-2 |
6 |
12 |
15 |
19 |
20 |
M-3 |
7 |
17 |
21 |
23 |
28 |
M-4 |
12 |
23 |
26 |
30 |
31 |
Akt. Reihenfolge |
2 |
3 |
1 |
5 |
9 |
M-1 |
1 |
6 |
10 |
15 |
17 |
M-2 |
6 |
12 |
15 |
16 |
21 |
M-3 |
7 |
17 |
21 |
26 |
28 |
M-4 |
12 |
23 |
26 |
27 |
32 |
Optimale Reihenfolge: |
2 - 9 - 3 - 1 - 5
|
Zykluszeit: |
31 |
|
|
|
|
Gantt-Diagramm:
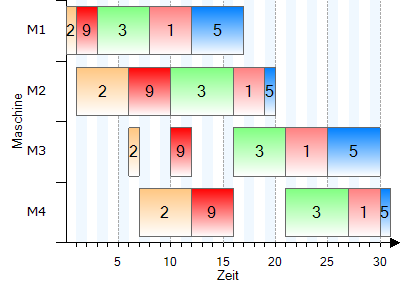
Die weiteren Iterationen (nur noch die Gantt-Diagramme): |
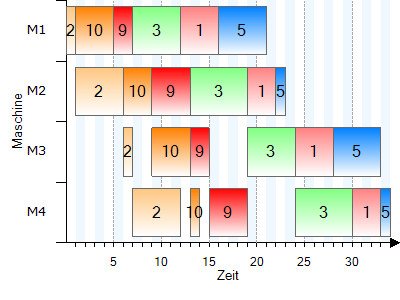
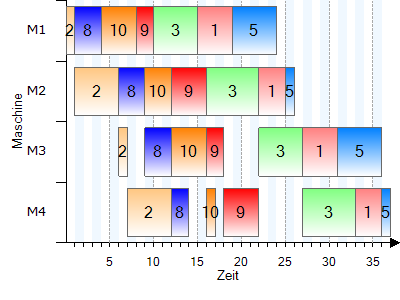
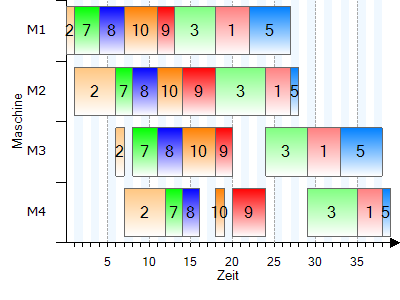
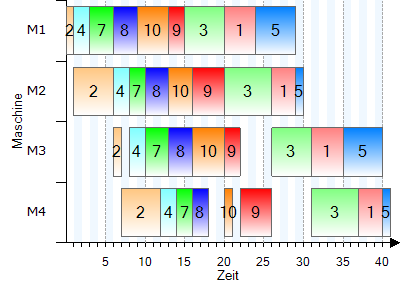
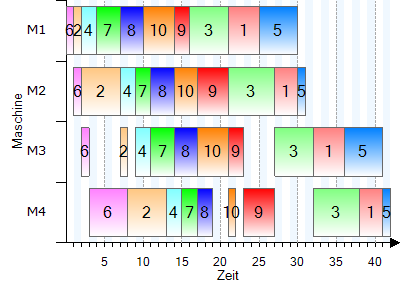
Die optimale Reihenfolge ist damit 6-2-4-7-8-10-9-3-1-5 mit einer Zykluszeit von 42 Zeiteinheiten.
Siehe auch ...
Literatur
| Günther, H.-O. und Tempelmeier, H. (2020). Supply Chain Analytics - Operations Management und Logistik. 13. Aufl., Norderstedt: Books on Demand. |
| Tempelmeier, H. (2020), Produuction Analytics. 6. Aufl., Norderstedt: Books on Demand. |
Tempelmeier, H. (2018). Supply Chain Management und Produktion. 6. Aufl.,
Norderstedt: Books on Demand. |