Ressourceneinsatzplanung, Projektplanung (RCPSP)
Die Methoden der Projektplanung kommen in mehreren Bereichen zum Einsatz:
bei der Planung von Großprojekten
bei Baustellenfertigung
bei der Ressourceneinsatzplanung im Rahmen eines PPS-Systems
Im Folgenden wird der letztgenannte Einsatzbereich, d.h. die Ressourceneinsatzplanung im Rahmen eines Systems zur Produktionsplanung und -steuerung beschrieben. Dabei gehen wir von einer Kleinserien- bzw. Werkstattproduktion aus. Die Ressourceneinsatzplanung schließt unmittelbar an die Losgrößenplanung an. Nachdem in der Losgroßenplanung die Produktionsaufträge gebildet worden sind, geht es in der Ressourceneinsatzplanung nun darum, die Aufträge zur Produktion freizugeben (Auftragsfreigabe) und konkreten Arbeitssystemen zur Bearbeitung zuzuweisen. Dabei müssen ebenso wie in der Losgrößenplanung die begrenzten Kapazitäten der Ressourcen berücksichtigt werden. Während sich die Losgrößenplanung oft nur auf die wichtigsten Erzeugnisse (z. B. A-Produkte) bezieht, die in einem Produktionssegment zu bearbeiten sind, müssen nun alle Produktionsaufträge – auch die Aufträge für B- und C-Produkte sowie Aufträge, die z. B. nur zur Auffüllung angegriffener Sicherheitsbestandsmengen gebildet worden sind – in die Überlegungen mit einbezogen werden.
Die Ressourceneinsatzplanung basiert auf den in der Losgrößenplanung festgelegten Eckterminen der Aufträge (bezogen auf Endprodukte, Baugruppen oder Einzelteile) sowie auf den Arbeitsplänen der Erzeugnisse. Ein Arbeitsplan ist eine Liste derjenigen Arbeitsgäange, die zur Herstellung eines bestimmten Erzeugnisses durchgeführt werden müssen. Aus der Reihenfolge der Arbeitsgänge im Arbeitsplan lassen sich auch die notwendigen Transportvorgänge ableiten. Weiterhin enthält der Arbeitsplan für jeden Arbeitsgang Angaben über die Bearbeitungszeit (Rüstzeit sowie Stückbearbeitungszeit). Zusammen mit der Losgröße kann man dann die gesamte Produktionsdauer eines arbeitsgangbezogenen Produktionsauftrages ermitteln. Dies ist die weiter unten verwendete Vorgangsdauer. Schließlich kann aus der Beschreibung eines Arbeitsgangs entnommen werden, ob dieser durch einen bestimmten Ressourcentyp ausgeführt werden muß oder ob evtl. auch alternative Ressourcen eingesetzt werden können.
Durch Zusammenführung der Informationen über der Erzeugnisstruktur, wie sie z.B. in einer Stückliste oder einem Gozintographen dokumentiert ist, und der Informationen, die in den Arbeitsplänen de einzelnen Vor-, Zwischen- und Endprodukte dokumentiert sind, erzeugt man ein Auftragsnetz (Erzeugnis- und Prozeßstruktur), das die Grundlage für die Terminplanung bildet. Dieses Auftragsnetz umfaßt in der Praxis in Abhängikeit vom Produktionsprogramm und der Länge des Planungszeitraums oft mehrere Tausend Vorgänge.
Die Aufgabe der Terminplanung besteht darin, für alle Aufträge, die im aktuellen Planungszeitraum fertiggestellt werden müssen, die Start- und Endtermine ihrer Bearbeitung an den einzelnen Ressourcen zu bestimmen und die Aufträge den Ressourcen zuzuordnen, falls alternative Zuordnungsmöglichkeiten bestehen.
Die Terminplanung ermittelt für jeden Arbeitsgang bzw. Auftrag den frühestmöglichen und den spätestzulässigen Start- und Endtermin. Sie bedient sich dabei der Rechenregeln der Netzplantechnik. In der betrieblichen Praxis wird in der Regeln in zwei Schritten vorgegangen. Zunächst werden in der sog. Durchlaufterminierung die Anfangs- und Endtermine der Aufträge (bzw. Vorgänge) unter Vernachlässigung der Kapazitäten der Ressourcen berechnet. Hierzu kann man die Rechenregeln der Netzplantechnik einsetzen, die sehr einfach zu implementieren sind. Ergebnis dieser Berechnungen sind frühestmögliche und spätestzulässige Start- und Endtermine sowie Pufferzeiten der einzelnen Aufträge bzw. auftragsbezogenen Arbeitsgänge.
Erst in einem nachfolgenden Planungsschritt werden in den meisten in der Praxis eingesetzten PPS-Systemen dann die sich aufgrund der zeitlichen Verteilung der Aufträge ergebenden Kapazitätsbelastungen den vorhandenen, oft knappen, Kapazitäten der Ressourcen gegenübergestellt. Treten Überlastungen der Ressourcen auf, dann ist der ermittelte Terminplan nicht zulässig, denn es wird zwangsläufig zu Überschreitungen der geplanten Fertigstellungstermine einzelner Aufträge kommen. Um dies zu vermeiden, versucht man im Rahmen eines anschließenden Kapazitätsbelastungsausgleichs, vorwiegend durch die zeitliche Verschiebung von Aufträgen einen zulässigen Terminplan zu erzeugen. Dies ist unproblematisch, solange die Verschiebungen innerhalb der verfügbaren Pufferzeiten möglich sind. Oft besteht diese Möglichkeit aber nicht.
Ein einfaches Beispiel soll die prinzipielle Vorgehensweise erläutern. Betrachten wir das folgende Auftragsnetz:
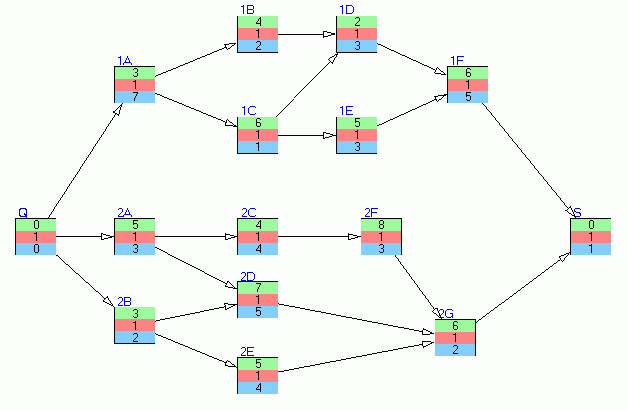
Jeder Vorgang wird durch einen Knoten mit den Angaben (Vorgangsdauer, Ressourcennummer, Ressourcenbedarf) dargestellt. Die Vorgangsbezeichnungen sind außen neben den Knoten angegeben. Die Kapazität der einzigen Ressource beträgt 10. Die Anwendung der MPM-Netzplantechnik ohne Berücksichtigung der Kapazität führt zu folgendem Terminplan und daraus resultierenden Kapazitätsbelastungen:
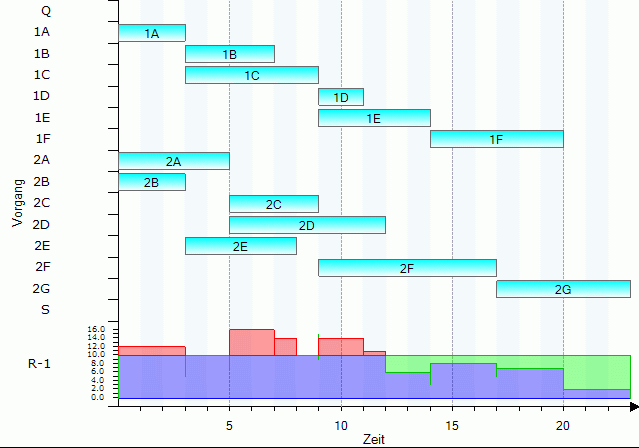
Wenn der gewünschte Fertigstellungstermin des Vorgangs 2G gleich 23 ist, dann ist dieser Terminplan nicht zulässig, da die Kapazität der Ressource in mehreren Perioden überschritten wird. In der Praxis versucht man in solchen Fällen, durch einen Kapazitätsbelastungsausgleich, bei dem die Arbeitsgänge zeitlich verschoben werden, einen zulässigen Terminplan zu erzeugen. Dies gelingt aber in den meisten Fällen nicht. Auch im vorliegenden Beispiel lassen sich die Überlastungen der Ressource nur beseitigen, wenn man einen späteren Fertigstellu ngstermin des Vorgangs 2G akzeptiert.
In der betrieblichen Praxis, bei einer größeren Anzahl von Vorgängen, die um die knappen Ressourcen konkurrieren, entsteht eine Problemkomplexität, die auch durch einen erfahrenen Planer nicht mehr zu übersehen ist. Die Folge sind ungeplante Terminabweichungen, die dann, wenn sie nicht ausschließlich Zwischenprodukte, sondern auch Endprodukte betreffen, zu einem Goodwill-Verlust auf Seiten der Kunden führen können.
Grundsätzlich muß die Trennung zwischen Durchlaufterminierung und nachfolgendem Kapazitätsbelastungsausgleich kritisch gesehen werden. Erfolgversprechender ist eine Vorgehensweise, die auf der folgenden mathematischen Modellierung des betrachteten Problems basiert. Die Grundstruktur der betrachteten Problemstellung kann sehr einfach mit einem Modell der Mehr-Projektplanung bei begrenzt verfügbaren Ressourcen (Resource-Constrained Project Scheduling Problem; RCPSP) abgebildet werden. Mit dieser Problemklasse beschäftigt sich die Wissenschaft seit vielen Jahrzehnten. Eine Version dieses Modells lautet:
$\begin{eqnarray} \mathrm{Minimiere }Z=\sum_{t={FEZ}_J}^{{SEZ}_J} {t\cdot x_{Jt}}} \end{eqnarray}$
unter den Nebenbedingungen
$\begin{eqnarray} \sum_{t={FEZ}_j}^{{SEZ}_j} {x_{jt}}=1 \qquad {j=1,2,...,J} \end{eqnarray}$
$\begin{eqnarray} \sum_{t=FEZ_h}^{SEZ_h} t \cdot x_{ht} \leq \sum_{t=FEZ_j}^{SEZ_j} (t-d_j) \cdot x_{jt} \qquad {j=1,2,...,J;\;h \in V_j} \end{eqnarray}$
$\begin{eqnarray} \sum_{j=1}^J {k_{jr}}\cdot \sum_{q=t}^{t+d_j-1} {x_{jq}} \leq K_r \qquad{r=1,2,...,R;\;t=1,2,...,T} \end{eqnarray}$
$\begin{eqnarray} x_{jt} \in \left\{ {0,1} \right\} \qquad {j=1,2,...,J;\; t=1,2,...,T} \end{eqnarray}$
Es bedeuten:
| $d_j$ | Dauer des Arbeitsgangs $j$ |
| $FEZ_j$ | frühestmöglicher Endtermin des Arbeitsgangs $j$ |
| $J$ | Anzahl der Arbeitsgänge $(j=1,2,...,J)$ |
| $k_{jr}$ | Kapazitätsbedarf des Arbeitsgangs $j$ bezüglich der Ressource $r$ je Periode |
| $K_r$ | Periodenkapazität der Ressource $r$ |
| $R$ | Anzahl der Ressourcen $(r=1,2,...,R)$ |
| $SEZ_j$ | spätestzulässiger Endtermin des Arbeitsgangs $j$ |
| $T$ | maximale angenommene Projektdauer |
| $V_j$ | Indexmenge der Vorgängerarbeitsgänge des Arbeitsgangs $j$ im Netzplan |
| $x_{jt}$ | Binärvariable, die den Wert 1 annimmt, wenn der Arbeitsgang $j$ in Periode $t$ beendet wird |
Die Zielfunktion minimiert den Fertigstellungszeitpunkt des letzten Arbeitsgangs (d.h., die Zykluszeit). Die erste Nebenbedingung verlangt, daß jeder Arbeitsgang beendet und damit natürlich auch durchgeführt werden muß. Die zweite Gruppe von Nebenbedingungen beschreibt die Vorgänger-Nachfolger-Beziehungen zwischen den Produkten. Auf der linken Seite steht der Fertigstellungszeitpunkt des Vorgangs $h$; auf der rechten Seite steht der Startzeitpunkt eines Nachfolgerarbeitsgangs $j$. Ist der Netzplan topologisch sortiert, d.h. ein Vorgängerarbeitsgang hat einen kleineren Index als der Nachfolgerarbeitsgang (d.h. die Vorgänge sind von links nach rechts aufsteigend nummeriert), dann stellt diese Beziehung sicher, daß die Arbeitsgänge in der richtigen zeitlichen Reihenfolge durchgeführt werden. Die nächste Gruppe von Nebenbedingungen garantiert, daß die Kapazitätsbeschränkungen eingehalten werden.
Die Kapazität der Ressource $r$ in Periode $t$ ist $K_r$. Es wird angenommen, daß es sich um eine sog. erneuerbare Ressource handelt. Das bedeutet, daß die Kapazität der Ressource in jeder Periode erneut in voller Höhe zur Verfügung steht. Im Gegensatz dazu steht die nicht-erneuerbare Ressource, die zu Beginn des Planungszeitraums verfügbar ist und dann in den folgenden Periode verbraucht wird. Auf diese Weise kann man z.B. ein finanzielles Budget oder auch einen gegebenen Materialbestand modellieren, der nach und nach während der Produktion verbraucht wird.
Die Beanspruchung der Ressource $r$ durch den Arbeitsgang $j$ pro Periode beträgt -- unabhängig von der Periode, in der der Arbeitsgang die Ressource belegt -- $k_{jr}$. Wir müssen nun einen Weg finden, um einen Zusammenhang zwischen den Variablen des Modells, d.h. der Fertigstellung eines Arbeitsgangs und der aus der Bearbeitung dieses Arbeitsgangs hervorgerufenen Kapazitätsbelastung in den davorliegenden Perioden herzustellen. Dazu überlegen wir uns Folgendes. Wird ein Arbeitsgang in einer Periode $q$ beendet ($x_{jq}=1$), dann muß er genau in den letzten $d_j$ Perioden vor der Periode $q$, also im Zeitabschnitt ($q-d_j+1,...,q-1,q$) bearbeitet worden sein.
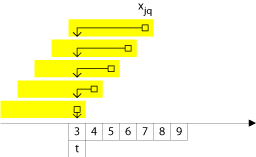
Wenn wir jetzt aber eine beliebige Periode $t$ betrachten, dann kann der Arbeitsgang $j$ in dieser Periode $t$ nur dann bearbeitet worden sein, wenn er im Zeitraum mit den Perioden $q=t,t+1,...,t+d_j-1$ beendet wird. Nur in diesen Perioden kommt es zu Ressoucrenbedarf. Für jede Periode $t$ müssen wir damit nur die Fertigstellungstermine des Auftrags $j$ im Bereich von $t$ bis $t+d_j-1$ betrachten. Dies wird durch die Kapazitätsrestriktion wiedergegeben.
Zur Lösung des Modells RCPSP sind in den letzten Jahren zahlreiche Lösungsverfahren entwickelt worden sind. Prinzipiell kann man das Modell natürlich mit einem Standard-Solver, z,B. CPLEX oder Gurobi, lösen. Dabei verwndet man üblicherweise ein Modellierungssystem, z.B. OPL oder AMPL, überträgt das Modell RCPSP in die Syntax des Modellierungssystems und startet dann den Solver. Dies ist allerdings nur für kleinere Probleme möglich. Leistungsfähiger sind spezialisierte Lösungsverfahren, die die spezielle Struktur des RCPSP ausnutzen und daher i.d.R. schneller als ein Standard-Solver sind. Aber auch diese Verfahren sind nicht für beliebig große Probleminstanzen einsetzbar.
Für größere Probleme, wie sie im Regelfall in der betrieblichen Praxis anzutreffen sind, existieren heuristische Lösungsverfahren, mit denen man in vielen Fällen sehr schnell einen guten und im Hinblick auf die Kapazitäten der Ressourcen zulässigen Terminplan erzeugen kann.
Die Anwendung eines heuristischen Verfahrens (implementiert im Produktions-Management-Trainer) ergibt z.B. folgenden zulässigen Plan:
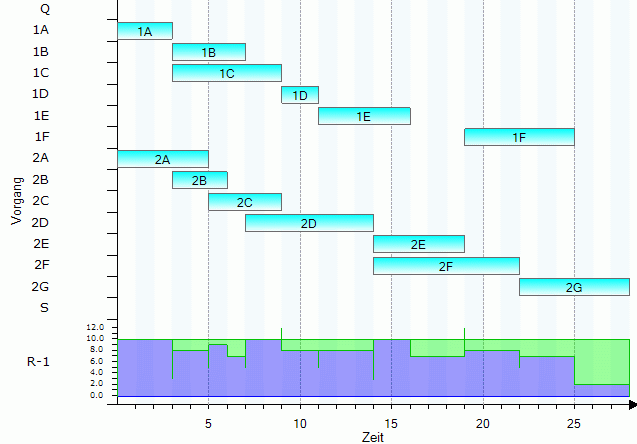
Hier kommt es zu keiner Überlastung der Ressourcen. Aber man erkennt, daß sich der Fertigstellungstermin des Arbeitsgangs 2G auf 28 erhöht hat.
Das Modell RCPSP läßt sich in der Praxis immer dann einsetzen, wenn das betrachtete Problem durch einen Netzplan abgebildet werden kann. Konzepte der Projektplanung, die durch das RCPSP abgebildet werden, können z.B. auch eingesetzt werden, wenn es darum geht, die Produktion komplexer Produkte au verschiedene Werke eines Unternehmens zuzuordnen. Unterhält z.B. ein Hersteller von Werkzeugmaschinen mehrere Fabriken mit beschränkten Kapazitäten (eine in Deutschland, die andere in China), dann kann die Entscheidung, in welcher Fabrik ein bestimmter Kundenauftrag (abgebildet durch ein Auftragsnetz) ausgeführt werden soll, mit Hilfe der Konzepte der kapazitätsorientierten Projektplanung getroffen werden. Weitere Anwendungsbeispiele finden sich in Tempelmeier(2010).
Siehe auch ...
Literatur
| Günther, H.-O. und Tempelmeier, H. (2020). Supply Chain Analytics - Operations Management und Logistik. 13. Aufl., Norderstedt: Books on Demand. |
| Tempelmeier, H. (2020). Analytics in Supply Chain Management und Produktion. 7. Aufl., Norderstedt: Books on Demand. |