
Discrete facility location
Given a fixed number of plants (selected from a set of potential locations)
with given capacities the subproblem of finding the cost-minimal assignment
of customer locations to these plants is solved with the help of the transportation
algorithm. The total costs (fixed costs of the selected plants and the optimal
transportation costs) are computed.
A potential plant location can be excluded from the set of selected
locations by setting it's capacity b(i) to zero. A value of b(i)>0 includes
the plant into the solution and increases the fixed total cost by the plant's
fixed costs.
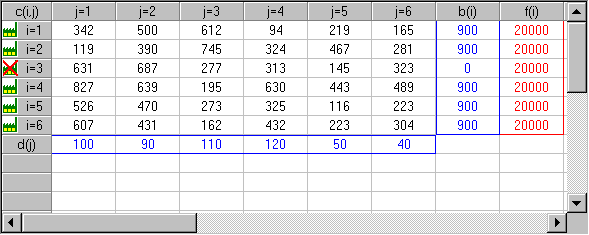
A value of b(i)>0 includes the location into the current cofiguration.
The optimal solution of the transportation subproblem
is depicted on a map. The red rectangles are the potential plant locations.
Green nodes are customer locations. The nodes may be moved with the mouse. 1)
Click on a node 2) Move the mouse to the desired location and click again. The
transportation cost coefficients may be comuted automatically (proportional
to the straight-line distances between the nodes).
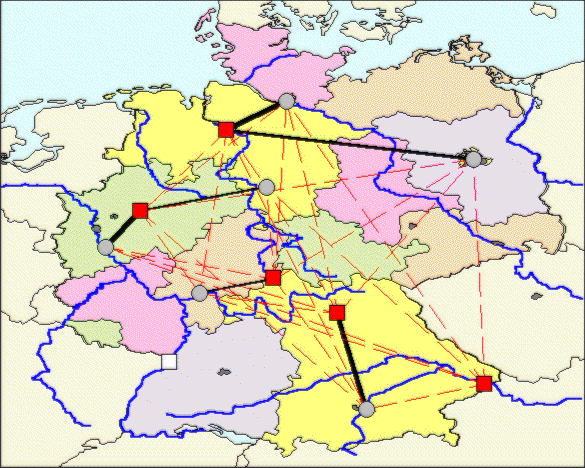
You can move the nodes (rectangles=potential locations; circles=demand
centers} on the map with the mouse. Optionally the transportation costs are
computed based on the straight-line distances.
Move the cursor over the nodes for more information.
All numbers must be integer. If the total demand is not equal the
total capacity of all locations included in a configuration, a dummy-location
or a dummy demand center is introduced with cost coefficients 9999.
Symbols:
| b(i) |
capacity of location i |
| d(j) |
demand quantity of demand center j |
| c(i,j) |
per unit transportation costs from location i to demand center j |
| f(i) |
fixed costs of potential location i |
The data may be saved in a file with the
standard extension *.sfl.
Literature:
- Krajewski/Ritzman (1996), chapter 8
|



