
3
5.4 Eine Lagrange-Heuristik
Literaturhinweis
Tempelmeier (2018), Aufgabe A1.4
5.4.1 Reformulierung
Reformulierung
Symbole
a
i
Kapazit¨at des potentiellen Standortes i
d
j
Nachfrage des Abnehmers j
c
u
ij
Transportkosten pro ME von i nach j
m
ij
Transportmenge von i nach j
γ
i
(
1 wenn Standort i gew¨ahlt wird,
0 sonst.
Reformulierung
Minimiere Z =
I
X
i=1
J
X
j=1
c
u
ij
· m
ij
+
I
X
i=1
f
i
· γ
i
J
X
j=1
m
ij
≤ a
i
· γ
i
∀i
I
X
i=1
m
ij
= d
j
∀j
γ
i
∈ {0, 1}, m
ij
≥ 0 ∀ij
18

Transformation I
x
ij
=
m
ij
d
j
I
X
i=1
m
ij
d
j
=
d
j
d
j
∀j
I
X
i=1
x
ij
= 1 ∀j
Transformation II
J
X
j=1
d
j
· x
ij
≤ a
i
·γ
i
∀i
Wegen
m
ij
= d
j
· x
ij
gilt
c
u
ij
·m
ij
⇒ c
u
ij
· d
j
· x
ij
c
ij
= c
u
ij
· d
j
Neue Formulierung
Neue Vari ablen und Kosten
c
ij
Transportkosten f¨ur den Gesamtbedarf des Abnehmers j vom Standort
i
x
ij
Anteil des Gesamtbedarfs des Abnehmers j, der vom Standort i
geliefert wird
Literaturhinweis
Falls Sie noch nichts von Dualit¨at geh¨ort haben, lesen Sie jetzt: Domschke and Drexl
(2005), Abschnitt 2.5 .1
19

Neue Formulierung
Modell P, Teil I
Minimiere Z =
I
X
i=1
J
X
j=1
c
ij
· x
ij
+
I
X
i=1
f
i
· γ
i
u. B. d. R.
J
X
j=1
d
j
· x
ij
≤ a
i
·γ
i
∀i
I
X
i=1
x
ij
= 1 ∀j Dualvariable: v
j
Neue Formulierung
Modell P, Teil II
γ
i
∈ {0, 1} alle i
x
ij
≥ 0 alle ij
Problem: Dualvariablen (Lenkpreise) v
j
• Einem Abnehmer wird zu wenig geliefert:
Belieferung verbilligen, v
j
erh¨ohen
• Ein Abnehmer wird zuviel geliefert:
Belieferung verteuern, v
j
senken
20

Modell LR
i
kontinuierliches (fractional) Knapsackproblem
Minimiere Z
D
i
(x|γ
i
= 1, v) =
J
X
j=1
(c
ij
− v
j
) ·x
ij
+ f
i
· 1
u. B. d. R.
J
X
j=1
d
j
· x
ij
≤ a
i
·1 ∀i
x
ij
≥ 0 ∀ij
Modell Knapsack (fractional)
allgemeine Form
Maximiere Z =
J
X
j=1
c
j
·x
j
bzw. Minimiere Z =
J
X
j=1
−c
j
·x
j
u. B. d. R.
J
X
j=1
a
j
· x
j
≤ b
x
j
≥ 0 j = 1, 2, . . . , J
Zum bi n¨aren Knapsack-Problem siehe auch:
http://www.advanced-planning.de/advancedplanning-191.html
Zum kontinuierlichen Knapsack-Problem siehe:
http://www.advanced-planning.de/advancedplanning-191a .html
Modell Knapsack (fractional)
L¨osung
L¨osung mit einem Greedy-Algorithmus:
r
j
=
c
j
a
j
relativer Zielbeitrag
Im vorliegenden Anwendungsfall ergibt sich f¨ur den Standort i:
r
ij
=
c
ij
− v
j
d
j
21
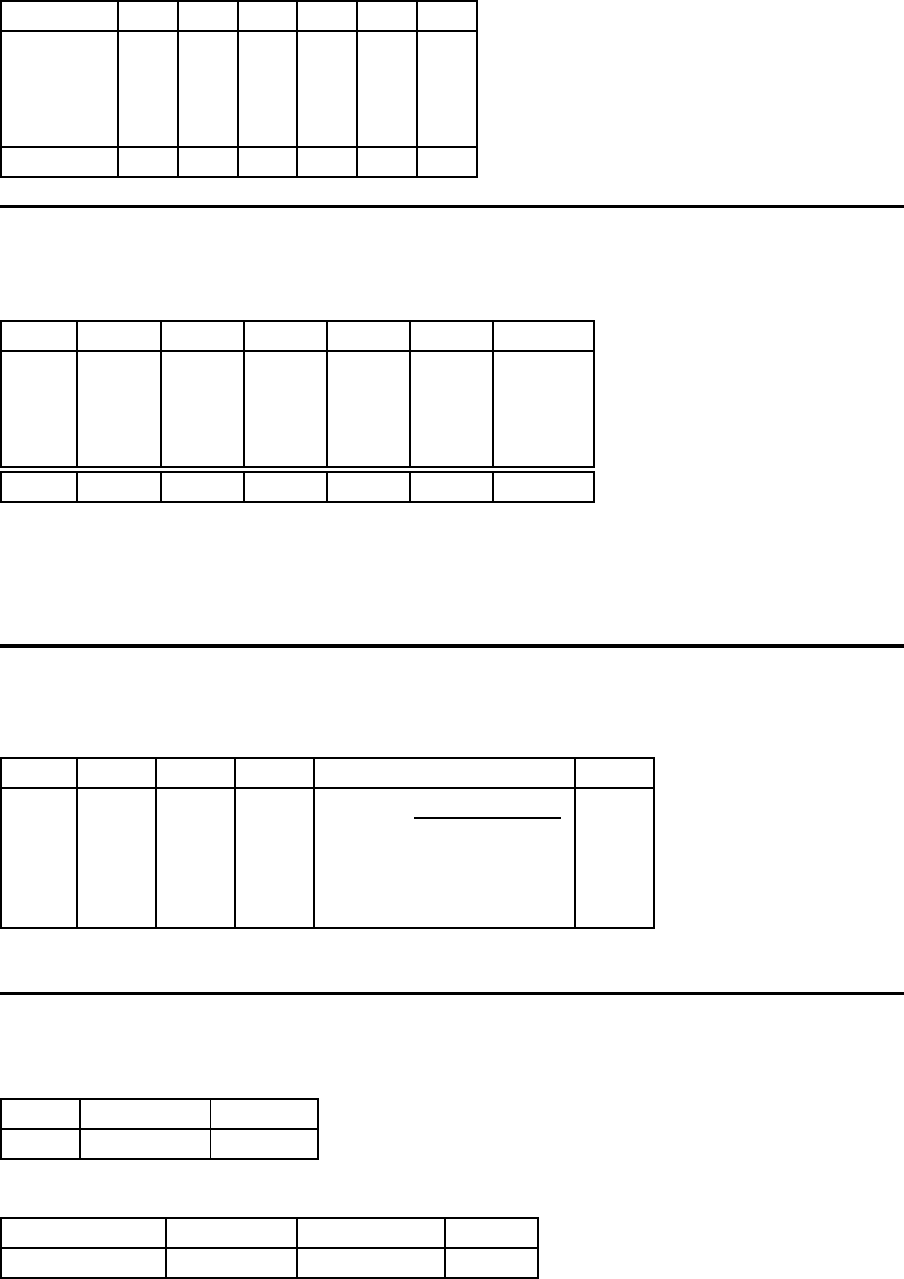
Transportkosten c
u
ij
pro Mengeneinheit
von nach 1 2 3 4 5 a
i
1 342 500 612 94 219 250
2 119 390 745 324 467 350
4 631 687 277 313 145 350
3 827 639 195 630 443 250
d
j
100 90 110 120 50
Startwerte der Dualvariablen v
j
c
u
ij
·d
j
j = 1 j = 2 j = 3 j = 4 j = 5
i = 1 34200 45000 67320 11280 10950
i = 2 11900 35100 81950 38880 23350
i = 3 63100 61830 30470 37560 7250
i = 4 82700 57510 21450 75600 22150 Summe
v
j
34200 45000 30470 37560 10950 158180
Guter Startwert f¨ur v
j
– zweitkleinster Wert je Spalte
Die obige Tabelle enth¨alt jetzt die Kosten f¨ur die Lieferung des gesamten Bedarfs des
Abnehmers j durch den Standort i.
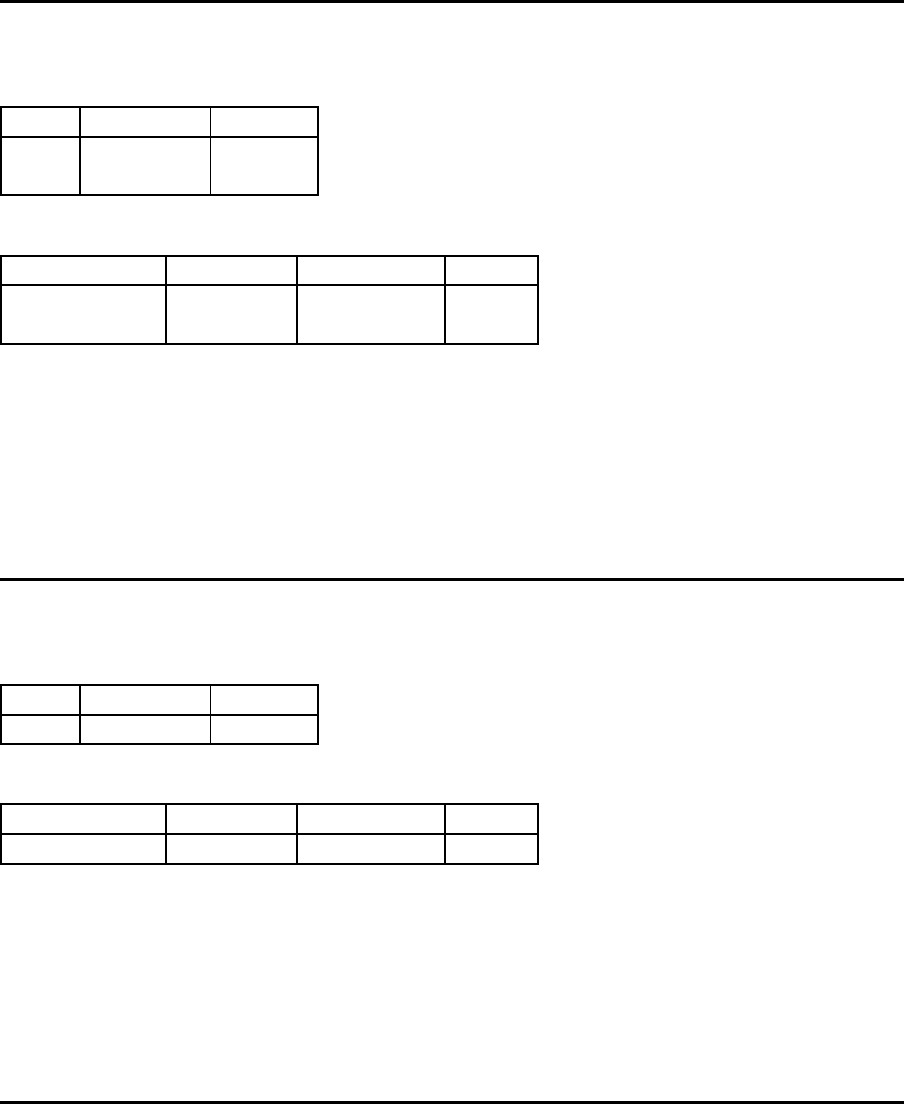
Iteration 1
Berechnung der r
ij
-Werte
j = 1 j = 2 j = 3 j = 4 j = 5
i = 1 0 0 0 −219 =
11280 − 37560
120
0
i = 2 -223 -110 0 0 0
i = 3 0 0 0 0 -74
i = 4 0 0 -82 0 0
Alle positiven r
ij
-Werte wurden gleich Null gesetzt. Warum?
Iteration 1
i = 1
Rang Abnehmer Zielwert
1 4 -219
Verteilung der Kapazit¨at
Restkapazit¨at Abnehmer Liefermenge Bedarf
250 4 120 120
22
X
j
(c
1j
− v
j
) · x
1j
= 112 80 −37560 = −26280
Iteration 1
i = 2
Rang Abnehmer Zielwert
1 1 -223
2 2 -110
Verteilung der Kapazit¨at
Restkapazit¨at Abnehmer Liefermenge Bedarf
350 1 100 100
250 2 90 90
X
j
(c
2j
− v
j
) · x
2j
= (c
21
−v
1
) + (c
22
− v
2
)
= (11900 − 34200) + (35100 −45000) = −32200
Iteration 1
i = 3
Rang Abnehmer Zielwert
1 5 -74
Verteilung der Kapazit¨at
Restkapazit¨at Abnehmer Liefermenge Bedarf
350 5 50 50
X
j
(c
3j
− v
j
) · x
3j
= 725 0 − 10950 = −3700
23
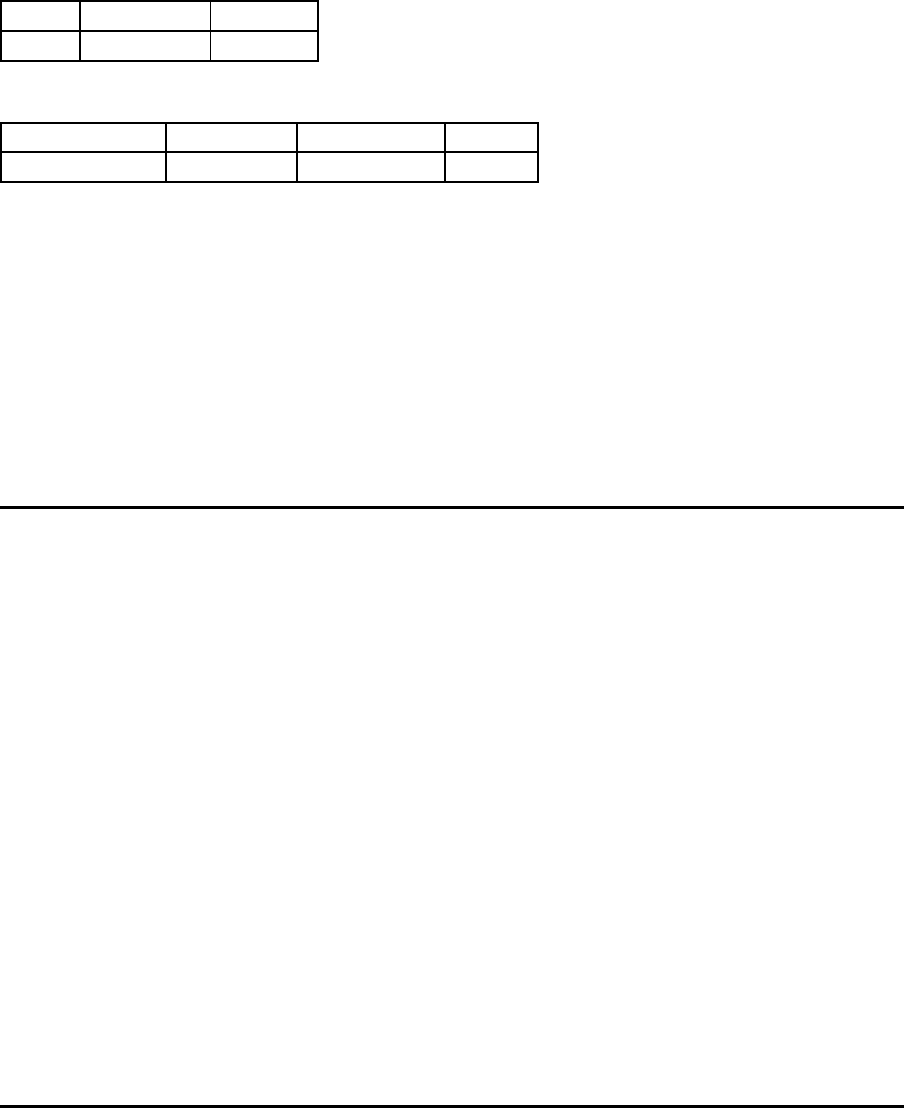
Iteration 1
i = 4
Rang Abnehmer Zielwert
1 3 -82
Verteilung der Kapazit¨at
Restkapazit¨at Abnehmer Liefermenge Bedarf
250 3 110 110
X
j
(c
4j
− v
j
) · x
4j
= 214 50 −30470 = −9020
Literaturhinweis
Bin¨a res Knapsackproblem: Domschke and Drexl (2005), Abschnitt 7.3.2
Modell LR
Bin¨ares Knapsackproblem
Minimiere Z
D
(γ) =
I
X
i=1
Z
D
i
· γ
i
u. B. d. R.
I
X
i=1
a
i
·γ
i
≥
J
X
j=1
d
j
γ
i
∈ {0, 1} ∀i
Aufgabe
L¨osen Sie das bin¨are Knapsackproblem des Beispiels mit AMPL oder OPL.
24
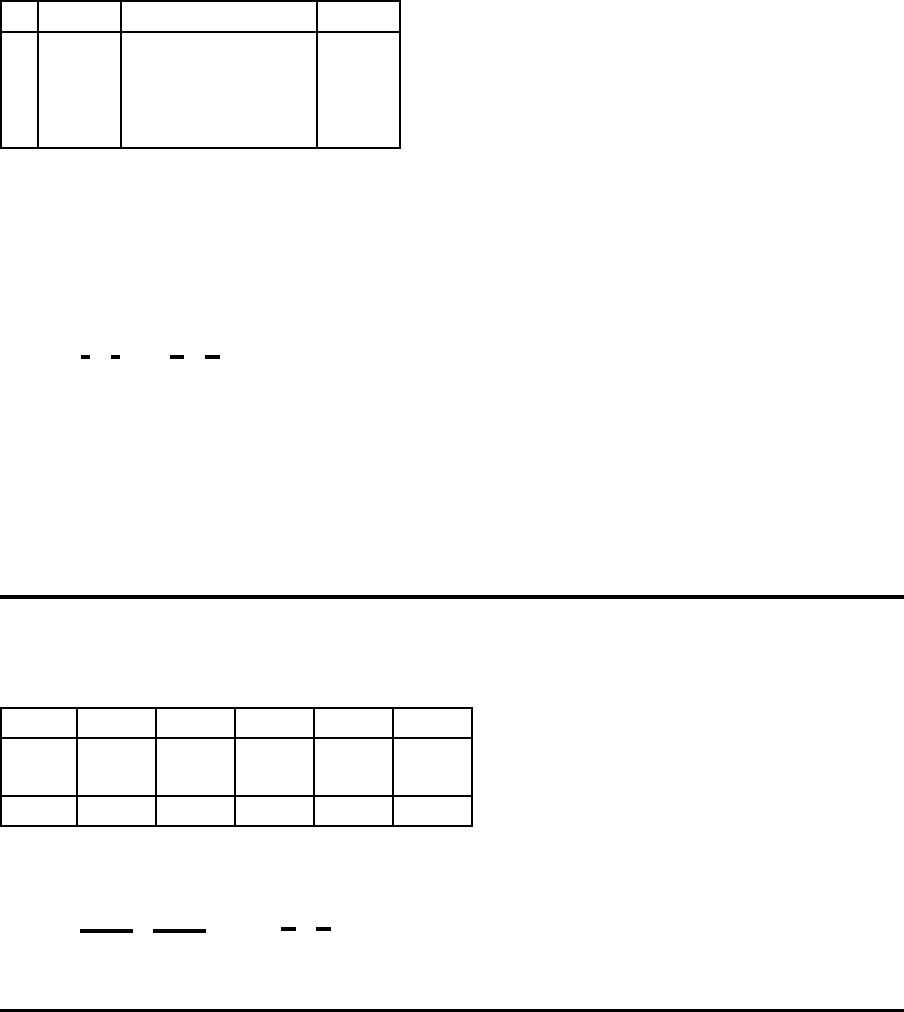
Modell LR
aktuelle Zielkoeffizienten des bin¨aren Knapsackprob l e ms
i f
i
P
j
(c
ij
− v
j
) · x
ij
s
i
1 50000 -26280 23720
2 50000 -32200 17800
3 50000 -3700 46300
4 50000 -9020 40980
L¨osung:
γ
1
= 1, γ
2
= 1, γ
3
= 0, γ
4
= 0
Lower Bound:
LB = 41520
|{z}
=
I
P
i=1
Z
D
i
+ 158180
| {z }
=
J
P
j=1
v
j
= 199700
Aufgabe
L¨osen Sie das klassische Transportpr oblem des Beispiels mit AMPL oder mit dem Produktions-
Management-Trainer.
Zul¨assige L¨osung
Klassisches Transportproblem
j = 1 j = 2 j = 3 j = 4 j = 5
i = 1 0 0 80 120 50
i = 2 100 90 30 0 0
d
j
100 90 110 120 50
Upper Bo und:
UB = 50000 + 50000
| {z }
Fixkosten
+ 1 40540
| {z }
T ransportkosten
= 240 540
Ver¨anderung der Dualvariablen I
b
j
= 1 −
I
X
i=1|γ
i
=1
x
ij
∀j
25
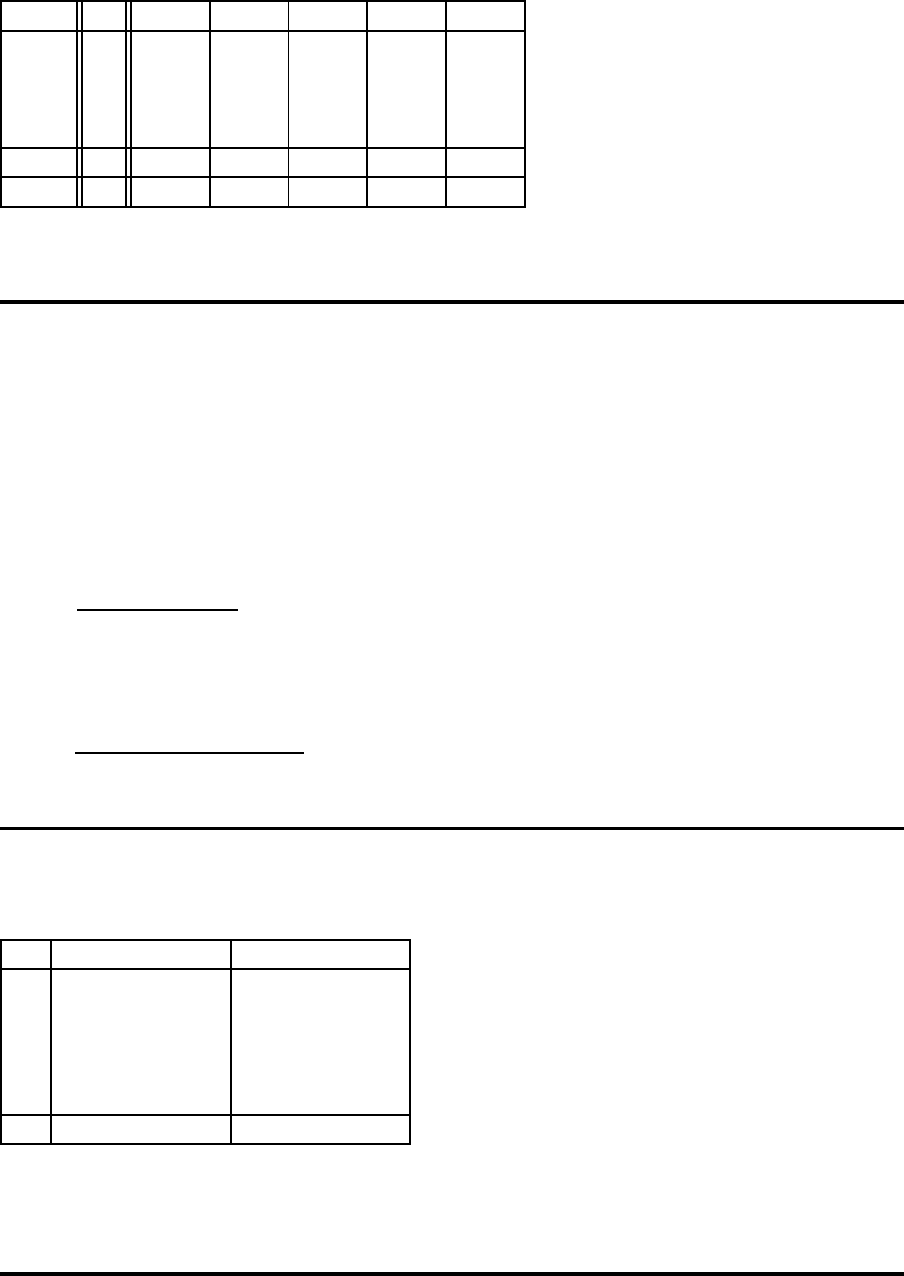
γ
i
j = 1 j = 2 j = 3 j = 4 j = 5
i = 1 1 0 0 0 1 0
i = 2 1 1 1 0 0 0
i = 3 0 0 0 0 0 1
i = 4 0 0 0 1 0 0
d
j
1 1 1 1 1
b
j
0 0 1 0 1
Nachfragerestriktionen pr¨ufen unter Ber¨ucksichtigung der beiden errichteten Standorte
(1 und 2).
Ver¨anderung der Dualvariablen II
Die folgende Vorgehensweise zur Anpassung der Dualvariablen hat sich bew¨ahrt.
v
j
:= v
j
+ δ · b
j
mit
δ = λ ·
1.05 · UB − LB
J
P
j=1
(b
j
)
2
δ = 2 ·
1.05 · 240540 − 199700
2
= 528 67
Neue Werte der Dualvariablen
zu Beginn der Iteration 2
j v
j
(Iteration 1) v
j
(Iteration 2)
1 34200 34200
2 45000 45000
3 30470 83337
4 37560 37560
5 10950 63817
P
158180 263914
Aufgabe
Interpretieren Sie die Ver¨anderung der D ualvariablen mit ¨okonomischen Argumenten.
26

Prinzipielle Vorgehensweise
Prinzipielle Vorgehensweise
1. Dualvariablen festlegen
2. Kontinuierliche Knapsackprobleme l¨osen (Auslieferungskosten)
3. Bin¨ares Knapsackproblem l¨osen (Standort auswa hl)
4. Klassisches Transportproblem l¨osen (zul¨assige L¨osung)
5. Wenn UB = LB, Stop. Wenn unter (3.) zul¨assige L¨osung gefunden wurde, Stop.
Sonst weiter bei (1.).
5.5 Single Sourcing
Problem: Jeder Abnehmer soll nur von einem Standort aus beliefert werden.
Literaturhinweis
Tempelmeier (2018), Aufgabe A1.5
5.6 Mehrere Kapazit¨atsklassen
Problem: Fixkosten variieren in Abh¨angigkeit von der Gr¨oße einer Fabrik. Degressiver
Kostenanstieg.
Literaturhinweis
Tempelmeier (2018), Aufgabe A1.6
5.7 Simple Plant Location Model f¨ur Au slieferungslager
Literaturhinweis
Helber (2014), Abschnitt 13.2
Problem: Es gibt eine Fabrik. Gesucht sind Standorte f¨ur Auslieferungslager, wo bei die
Transporte von der Fabrik zu den Lagerstandorten mit ber¨ucksichtigt werden m¨ussen.
Modell STANDORT
AL
Symbole
b
i
Kapazit¨at des Lagerstandorts i
ca
i
Transportkosten zwischen der Fabr ik und den potentiellen
Lagerstandorten (i = 1, 2, ..., I)
c
ij
Transportkosten zwischen Lagerstandort i und Abnehmerzentrum j
(pro Mengeneinheit)
d
j
Bedarfsmenge des Abnehmerzentrums j
f
i
Fixkosten pro Jahr am Lagerstandort i
I Anzahl der potentiellen Lagerstandorte (i = 1, 2, ..., I)
J Anzahl der Abnehmerzentren (j = 1, 2, ..., J)
27

Modell STANDORT
AL
Minimiere Z =
I
X
i=1
f
i
· γ
i
+
I
X
i=1
J
X
j=1
(ca
i
+ c
ij
) · x
ij
u. B. d. R.
I
X
i=1
x
ij
= d
j
j = 1, 2, ..., J
J
X
j=1
x
ij
≤ b
i
· γ
i
i = 1, 2, ..., I
x
ij
≥ 0 i = 1, 2, ..., I; j = 1, 2 , ..., J
Modell STANDORT
AL
γ
i
∈ {0, 1} i = 1, 2, ..., I
28