Dynamische Losgrößen- und Reihenfolgeplanung - Das BACADD-Verfahren von Haase
Die Aufgabe der Losgrößenplanung ist es, festzulegen, wie viele Mengeneinheiten eines Produkts auf einmal, d.h. mit einem Rüstvorgang, produziert werden sollen und wann dies geschehen soll. Dieses Problem wird seit mehr als 100 Jahren in der Literatur diskutiert. In der ursprünglichen Modellierung des sog. klassischen Losgrößenproblems wird von einer konstanten und kontinuierlich auftretenden Nachfrage(-rate) ausgegangen. Dies führt zu dem bekannten Sägezahn-ähnlichen Verlauf des Lagerbestands, der die Grundlage für die Berechnung der Lagerkosten bildet. Da sich das wirkliche Geschäftsleben aber nicht auf einer kontinuierlichen Zeitachse abspielt, sondern in Monate, Wochen, Arbeitstage, Schichten, Stunden oder Minuten eingeteilt ist, und da Zinskosten in der Finanzwelt nicht kontinuierlich, sondern i.d.R. täglich berechnet werden, wurde von Wagner und Whitin im Jahre 1958 eine Modellformulierung mit einer diskreten Zeitachse und periodenbezogenen Nachfragemengen vorgestellt. Ein Losgrößenmodell mit diskreter Zeitachse bezeichnet man als dynamisches Losgrößenmodell. Dadurch wird es auch möglich, im Zeitablauf sich verändernde Nachfragemengen (auch die Periodennachfragemenge Null) zu berücksichtigen. Diese Abbildung des Nachfrageverlaufs korrespondiert mit den in der Praxis eingesetzten Prognoseverfahren.
Das Modell von Wagner und Whitin unterstellt unbeschränkte Kapazitäten. Bei dieser Annahme entsteht ein Losgrößenproblem allerdings erst dann, wenn mit der Produktion eines Loses (oder der Bestellung einer Produktmenge bei einem Lieferanten) fixe Kosten verbunden sind. Ist das nicht der Fall, dann kann man einfach nachfragesynchron (just-in-time oder in amerikanisch L4L wie lot-for-lot) unter Vermeidung von Lagerkosten produzieren und hat folglich auch kein Optimierungsproblem.
In der industriellen Praxis spielen Fixkosten aber oft keine oder nur eine untergeordnete Rolle - sie sind oft nicht einmal bekannt. Beispielsweise läßt sich kaum beziffern, wie hoch die mit einem Rüstvorgang an einer Maschine verbundenen Fixkosten sind, wenn der Rüstvorgang durch einen Mitarbeiter durchgeführt wird, der ausreichend Zeit hat und ohnehin fest angestellt ist. Stattdessen ist mit der Vorbereitung einer Maschine für die Produktion normalerweise eine Rüstzeit verbunden, während der die Maschine nicht produktiv arbeitet, sondern nur abwartet, bis sie mit der Produktion beginnen kann. Je häufiger gerüstet wird, umso mehr produktiv nutzbare Zeit (Kapazität) der Maschine geht verloren. Das ist kein Problem, wenn die Kapazitätsauslastung so niedrig ist, daß es nie zu einer Engpaßsituation kommt.
Ist die Kapazität aber nicht unbegrenzt verfügbar, dann muß dies in der Losgrößenplanung berücksichtigt werden. Versucht man nun, Kapazitätsüberschreitungen infolge zu häufigen Rüstens dadurch zu vermeiden, daß man jeden Rüstvorgang mit Rüstkosten "bestraft", dann führt dies nur dann zum optimalen Produktionsplan bzw. zu optimalen periodenbezogenen Losgrößen, wenn man die periodenbezogenen optimalen Strafkosten kennt. Diese hängen aber davon ab, wie knapp die Kapazität in den einzelnen Perioden ist. Bei dynamischer, d.h. periodenbezogener Nachfrage, ändert sich die Knappheit der Kapazität aber von Periode zu Periode aufgrund der Schwankungen der Nachfragemengen und in Abhängigkeit von den eingeplanten Losgrößen. Das heißt, um die optimalen Losgrößen bestimmen zu können, muß man die optimalen Rüstkosten kennen. Diese kennt aber aber erst, wenn man die optimalen Losgrößen bestimmt hat und man sagen kann, in welchen Perioden die Kapazität knapp ist.
Bei beschränkter Kapazität kommen wir mit den beiden genannten unkapazitierten Losgrößenmodellen - unabhängig davon, ob die Zeitachse kontinuierlich oder diskret modelliert wird - also nicht weiter. Das wurde in der betriebswirtschaftlichen Forschung schon vor einigen Jahrzehnten erkannt und hat zu einer großen Anzahl unterschiedlicher dynamischer Losgrößenmodelle geführt, die die begrenzten periodenspezifischen Kapazitäten einer betrachteten Ressource mit berücksichtigen.
All diese Modelle bilden im Prinzip dasselbe Problem ab, nämlich die ursprünglich von Ford W. Harris bereits 1913 formulierte Frage "How many parts to make at once" (Factory, The Magazine of Management, Volume 10, Number 2, February 1913, pp. 135–136, 152). Die dynamischen Losgrößenmodelle unterscheiden sich nun vor allem dadurch, wie grob sie die Zeitachse modellieren. Je kleiner die Periodeneinteilung ist, umso genauer kann man das tatsächliche Produktionsgeschehen, also nicht nur die Losgrößen, sondern u.U. auch die Reihenfolgen, in der die produktspezifischen Lose bearbeitet werden, bestimmen. Die Wahl der Periodenlänge wurde in der Vergangenheit auch von der numerischen Lösbarkeit der resultierenden Modelle bestimmt. Denn das Ziel der Modellierungsanstrengungen ist es ja, gemischt-(kontinuierlich)- ganzzahlige Modelle (sog. Mixed-Integer-Modelle, MIP-Modelle) zu finden, die mit einem kommerziellen Standard-Solver in vertretbarer Rechenzeit gelöst werden können.
Je feiner die Periodeneinteilung ist, desto mehr binäre Entscheidungsvariablen enthält ein solches gemischt-ganzzahliges Optimierungsmodell. Dies hat einen erheblichen Einfluß auf die Rechenzeit, die für die optimale Lösung verbraucht wird.
In Abhängigkeit davon, ob in einer Periode beliebig viele Lose eingeplant werden können oder nicht, unterscheidet man Makroperioden-Modelle (big-bucket models) von Mikroperioden-Modellen (small-bucket models). Bei einem Makroperioden-Modell können beliebig viele Lose in einer Periode produziert werden (bis die Kapazität erschöpft ist). Im einfachsten Fall kann man aus der optimalen Lösung eines Makroperiodenmodells nur die Losgrößen entnehmen. Eine Aussage über die Produktionsreihenfolge der Lose innerhalb einer Makroperiode wird nicht getroffen. (Anmerkung: Allerdings gibt es Varianten von Makroperioden-Modellen, bei denen zumindest das erste und das letzte in einer Periode produzierte Produkt festgelegt werden, so daß man dann periodenübergreifende Rüstzustände berücksichtigen kann.)
Mit einem Mikroperioden-Modell dagegen wird neben den Losgrößen auch die Produktionsreihenfolge festgelegt. Das ist aber nur möglich, wenn man die Periodenlängen so festlegt, daß man die Kontrolle über den Produktionsbeginn und das Produktionsende eines jeden Loses hat. So kann man z.B. eine sehr feine Periodeneinteilung wählen und mit Hilfe von Entscheidungsvariablen in dem Losgrößenmodell festlegen, daß in jeder Periode genau ein Produkt produziert wird. Eine andere Modellvariante geht von der Vorstellung aus, daß in jeder Periode höchstens einmal umgerüstet wird. In diesem Fall können maximal zwei Produkte produziert werden: Ein Produkt am Periodenanfang (mit Übernahme des Rüstzustands der Maschine aus der Vorperiode) und ein Produkt, das nach einer Umrüstung der Maschine am Ende der Periode produziert wird.
Das als PLSP (Proportional Lotsizing and Scheduling Problem) bezeichnete Losgrößenmodell ist ein solches Losgrößen- und Reihenfolgemodell, mit dem sowohl die Losgrößen der Produkte als auch deren Produktionsreihenfolge festgelegt werden. Dieses Modell geht von im Vergleich zur Produktionsdauer eines Produkts kurzen Perioden aus (Mikroperiodenmodell, small-bucket Modell) und ermöglicht, falls die Kapazität einer Periode nicht voll durch die Produktion eines Produkts verbraucht wird, die Produktion eines zweiten Produkts. Die Grundbedingung des PLSP in seiner ursprünglichen Form lautet also: In jeder Periode darf höchstens ein Produktwechsel erfolgen. Bei ausreichend kurzen Perioden kann man damit beliebige Produktionspläne erzeugen.
In der ursprünglichen, von Knut Haase vorgeschlagenen Form des Modells wurden Rüstzeiten vernachlässigt. Wird in einer Periode die Kapazität vollständig durch die Produktion zweier Produkte ausgenutzt, dann ist die Losgröße des ersten Produkts proportional zum Zeitpunkt der Umrüstung. Beispiel: Periodenlänge 60 Minuten. Umrüstung nach 40 Minuten. Losgröße Produkt 1: 40; Losgröße Produkt 2: 20.
Das PLSP sieht vor, daß ein Los über mehrere Perioden hinweg produziert werden kann. Die Losgröße für ein Produkt ergibt sich aus den Produktionsmengen aufeinanderfolgender Perioden. Rüstkosten fallen nur einmal zu Beginn der Produktion mit der Vorbereitung der Ressource (Maschine) für das betreffende Produkt an. Das muß nicht die Produktionsperiode sein, in der mit der Produktion begonnen wird, sondern kann u.U. auch schon vorher (Ende der Vorperiode) passieren. Für die Modellierung benötigt man neben den üblichen (binären) Rüstvariablen eine zusätzliche Variable, die den Rüstzustand der Ressource am Ende einer Periode wiedergibt. Eine PLSP-Lösung determiniert somit einen genau definierten Produktionsablauf mit fixierten Produktionsstart- und -endterminen.
Beim klassischen CLSP (Capacitated Lot Sizing Problem), das die Produktion vieler Produkte in einer Periode ermöglicht, ist die Periodenlänge im Vergleich zu den Produktionsdauern der Produkte deutlich größer. Daher bezeichnet man das CLSP auch als big-bucket model bzw. Makroperiodenmodell. Das bedeutet nicht, daß die Periodenlänge im PLSP absolut betrachtet immer sehr kurz ist. Sie kann auch eine Woche oder länger sein. Es ist jedoch höchstens ein Produktwechsel in einer Periode vorgesehen.
Die feine Periodeneinteilung des PLSP dient vor allem dazu, neben den Losgrößen auch die Reihenfolgen zu bestimmen. Anders als in Makroperioden-Modellen kann man im PLSP nicht für jedes Produkt in jeder Periode Nachfrage vorsehen, da dann wegen der Beschränkung von maximal 2 Losen pro Periode keine zulässige Lösung des Modells existiert. Statt dessen kann man virtuelle Makroperioden bzw. Nachfrageperioden einführen, indem man z.B. in jeder dritten Mikroperiode Nachfragemengen einplant und in den Mikroperioden dazwischen keine Nachfrage vorsieht. Das zeigt die folgende Tabelle für ein Beispiel mit 12 Mikroperioden und 4 virtuellen Makroperioden, in der $d_{kt}$ die Nachfragemenge des Produkts $k$ in Periode $t$ ist und $b_t$ die Periodenlänge in Periode $t$ beschreibt.
| $d_{kt}$ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | - | - | 10 | - | - | 80 | - | - | 30 | - | - | 10 |
| 2 | - | - | - | - | - | - | - | - | 40 | - | - | 80 |
| 3 | - | - | 30 | - | - | 40 | - | - | - | - | - | 20 |
| 4 | - | - | - | - | - | - | - | - | 20 | - | - | 30 |
| 5 | - | - | - | - | - | 90 | - | - | - | - | - | 10 |
| $b_t$ | 50 | 50 | 50 | 50 | 50 | 50 | 50 | 50 | 50 | 50 | 50 | 50 |
Die optimale Lösung zeigt das folgende Bild.
In diesem Modul wird das PSLP mit dem heuristischen BACADD-Verfahren von Haase gelöst. Es handelt sich um ein heuristisches Lösungsverfahren, in dessen Verlauf eine große Anzahl von Produktionsplänen nach einem systematischen Konstruktionsmuster unter Verwendung von Zufallszahlen aufgebaut wird und dann der beste Plan ausgewählt wird. Bei jeder Ausführung versucht die BACADD-Heuristik, eine zulässigen und möglichst kostengünstigen Produktionsplan zu konstruieren. Falls kein zulässiger Plan gefunden wird, kann die Heuristik erneut (mit anderen Zufallszahlen) ausgeführt werden.
Siehe hierzu im Detail Tempelmeier(2020a).
Symbole:
| d(k,t) | Bedarfsmenge des Produkts k in Periode t |
| s(k) | Rüstkostensatz des Produkts k |
| h(k) | Lagerkostensatz des Produkts k |
| tb(k) | Stückbearbeitungszeit des Produkts k |
In den Optionen kann festgelegt werden, ob der Verfahrensablauf detailliert protokolliert werden soll oder ob nur die Ergebnisse ausgegeben werden sollen. Darüberhinaus kann zu Testzwecken durch die Option der manuellen Produktauswahl in den Verfahrensablauf eingegriffen werden.
Die Ergebnisse werden tabellarisch und in Form eines Gantt-Diagramms angezeigt:
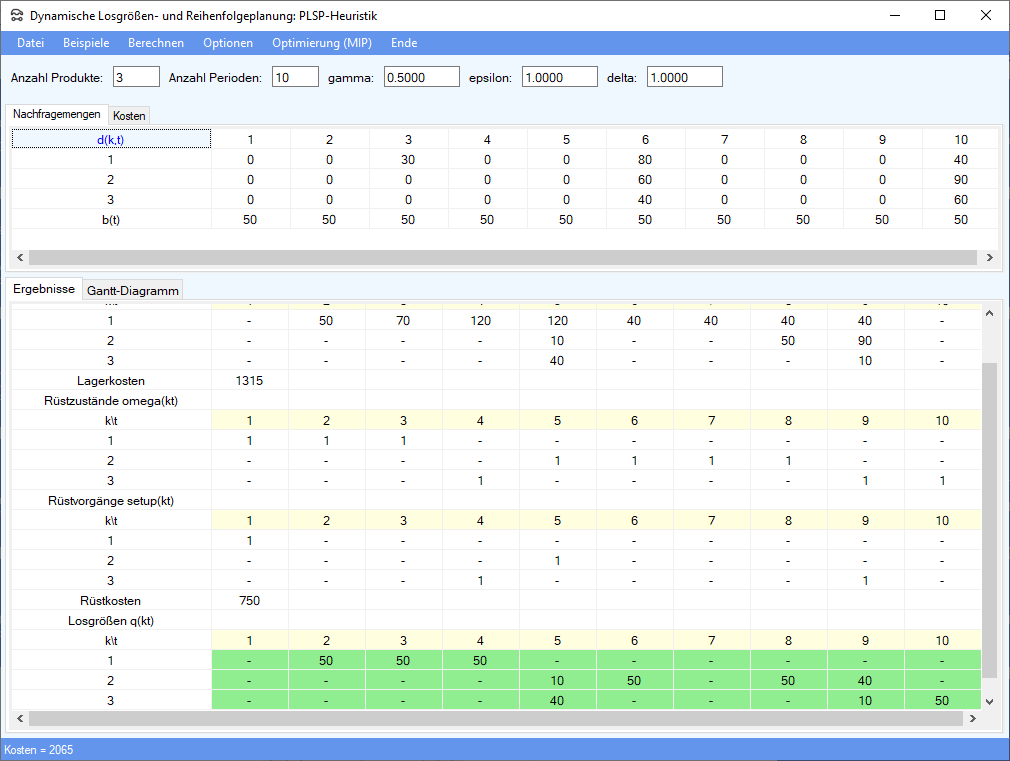
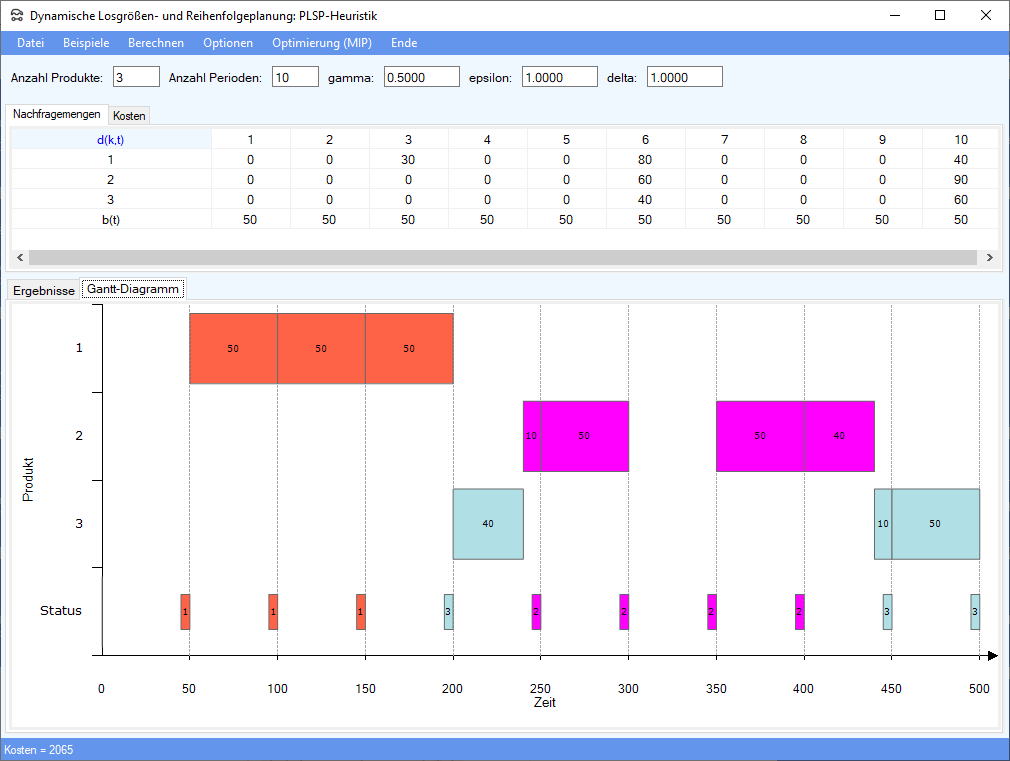
Es kann passieren, daß bei einem Durchlauf des BACADD-Verfahrens keine Lösung gefunden wird. Es erscheint dann eine Meldung mit einem entsprechenden Hinweis. In diesem Fall kann man das Verfahren nochmal ausführen. Da jedesmal mit anderen Zufallszahlen gerechnet wird, findet man dann möglicherweise eine zulässige Lösung.
Durch mehrmaliges Betätigen des Berechnen-Menüpunkts können mit unterschiedlichen Zufallszahlen auch unterschiedliche zulässige Produktionspläne erzeugt werden. Man verwendet dann sinnvollerweise den Plan mit den niedrigsten Kosten.
- Haase, Knut, Lotsizing and Scheduling for Production Planning, Berlin(Springer) 1994
- Tempelmeier(2020a)
Datenschutz | © 2021 POM Prof. Tempelmeier GmbH | Imprint