Warteschlangenmodelle

Es werden die Leistungskenngrößen verschiedener einstufiger Warteschlangensysteme berechnet. Diese Kenngrößen können zur Analyse von einstufigen Produktionsprozessen eingesetzt werden, in denen Zufallsgrößen eine große Rolle spielen. So kann man beispielsweise in der Werkstattproduktion eine einzelne Maschine betrachten, an der in unregelmäßigen zeitlichen Abständen Aufträge für unterschiedliche Produkte mit unterschiedlichen Rüst- und Bearbeitungszeiten eintreffen. In Abhängigkeit von den Wahrscheinlichkeitsverteilungen der Zwischenkunftszeiten und der Rüst- und Bearbeitungszeiten der Aufträge kann dann mit Hilfe der Wartschlangentheori die mittlere Durchlaufzeit, den mittleren Lagerbestand und andere interessierende Kenngrößen berechnen.

Sie sind aber auch für Analyse mehrstufiger Systeme interessant, wenn die Stationen unabhängig voneinander analysiert werden können (vgl. M/M/1-System und GI/G/1-System bei der Mehrproduktfließfertigung). Jede Station für sich stellt dann ein Warteschlangensystem dar, wie es hier behandelt wird.

Die hier betrachteten Kenngrößen werden in den meisten Lehrbüchern zum Operations-Research bzw. zur Warteschlangentheorie hergeleitet.

Symbole:

Rho	Auslastung
Ls	Anzahl der Kunden (Werkstücke, Paletten, etc.) im System
Lq	Anzahl der Kunden (Werkstücke, Paletten, etc.) im System
Ws	mittlere Durchlaufzeit durch das System
Wq	mittlere Wartezeit in der Warteschlange
P(n)	Wahrscheinlichkeit n Kunden im System vorzufinden, P0=P(0)

Zur Charakterisierung der Warteschlangenmodelle wird die folgende Kendall/Lee/Taha-Notation verwendet: (a/b/c):(d/e/f)

Dabei bedeuten:

a	Verteilung der Zwischenankunftszeiten
b	Verteilung der Bedienungszeiten
c	Anzahl von Bedienungseinheiten (Server) an einer Station
d	Warteschlangendisziplin (Prioritätsregel)
e	maximal zulässige Anzahl von Kunden (Werkstücken, Paletten, etc.) im System
f	Anzahl der (potentiellen) Kunden, Größe der Zugangsquelle

Für die Parameter a und b, die die Verteilungen festlegen, sind folgende Abkürzungen üblich:

M	Exponentialverteilung (Poisson- oder Markov-Verteilung)
D	deterministisch bestimmte Zeiten
Ek	Erlang- oder Gamma-Verteilung (mit Parameter k)
GI	allgemeine, unabhängige Verteilung (General Independent Distribution)
G	allgemeine Verteilung (General Distribution)

Beispiele für Bedienungsdisziplinen sind:

GD	allgemeine Disziplin (General Disziplin)
FCFS	(First Come First Served)
LCFS	(Last Come First Served)

Ansicht:

Literatur:

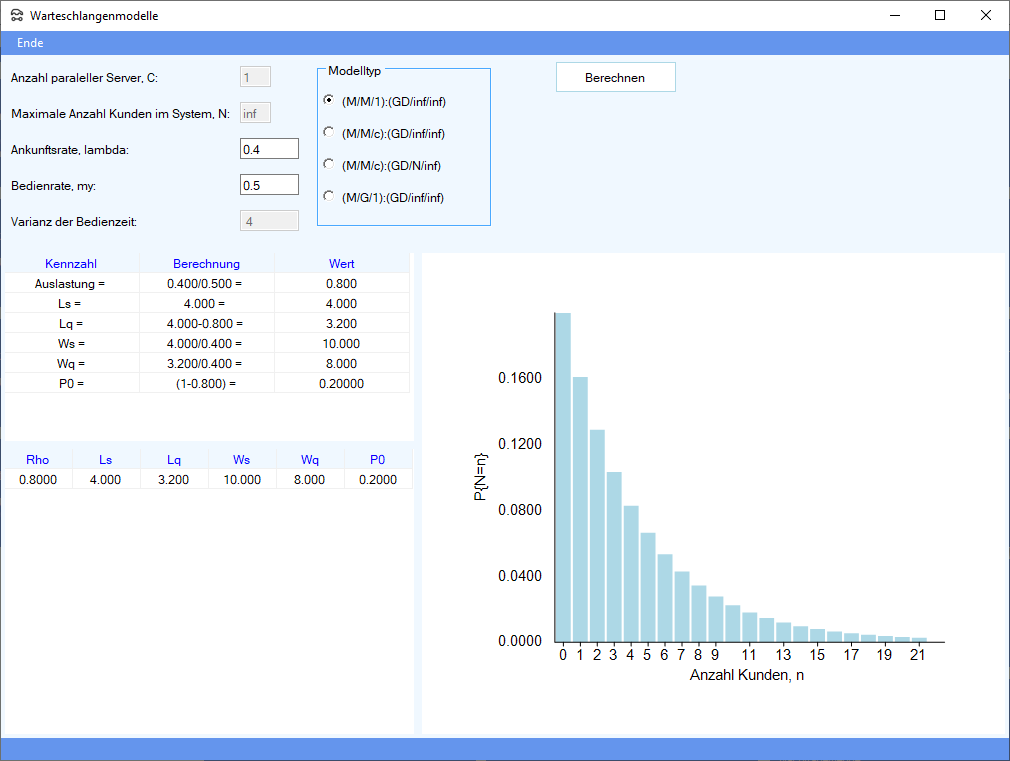
- Taha (2003)