
7_b
15 Pufferoptimierung
15.1 Einf¨uhrung
Entscheidungsvariablen
• Puffergr¨oßen
• Anzahl Server (Maschinen) pro Station
• Bearbeitungszeit pro Stat ion
• Kombinationen
Fragestellungen
• Die Anzahl Puffer beeinflußt die Produktionsrate
• Die Verteilung der Puffer beeinflußt die Produktionsrate
Daraus folgen die Fragen:
• Wie viele Pufferpl¨atze werden insgesamt ben¨otig t ?
• Wie sollen die Pufferpl¨atze Pufferpl¨atze auf die Stationen verteilt werden?
15.2 Greedy-Verfahren
Wenn die Puffergr¨oßen einen Einfluß auf die Produktionsrate haben, dann stellen sich
folgende Fragen:
Wie viele Pufferpl¨atze sollen in einem Fließproduktionssystem vorgesehen
werden, damit eine angestrebte Produktionsrate erreicht wird?
Wie sieht die optimale Verteilung der Pufferpl¨atze auf die Stationen aus?
Ist es optimal, an allen Stationen dieselbe Puffergr¨oße vorzusehen oder ist es
g¨unstiger, eine ungleichm¨aßige Verteilung der Puffer zu w¨ahlen?
87

Diese Frage soll anha nd eines Beispiels n¨aher betrachtet werden.
Nehmen wir an, die Stationen eines Fließproduktionssystems mit M = 5, b
m
= 10,
CV
m
= 0.3 (identische Stationen) sollen durch Puffer entkoppelt werden. Angenommen,
es steht eine gegebene Gesamtanzahl von N = 12 Pufferpl¨atzen zur Verf¨ugung, die nun
auf die einzelnen Stationen verteilt werden soll. Sollen diese Puffer konzentriert plaziert
oder gleichm¨aßig zwischen allen Station verteilt werden?
Die folgende Tabelle zeigt die Entwicklung der Produktionsrate bei unterschiedlichen
Allokationen dieser 12 Pufferpl¨atze auf die vier Pufferbereiche.
Prod.-Rate 1 2 3 4 5
0.09553 – 3 3 3 3
0.09528 – 4 3 3 2
0.09428 – 5 3 3 1
0.09116 – 6 3 3 0
0.09029 – 7 3 2 0
0.09554 – 2 4 4 2
Die gr¨o ßte Produktionsrate wird also erreicht, wenn man die Puffer so gleichm¨aßig wie
m¨oglich auf die Pufferbereiche verteilt. Man sollte versuchen, durch die Anordnung der
Puffer m¨oglichst gleichstarke Segmente zu schaffen.
Soll ein einzelner Pufferplatz eingef ¨ugt werden, da nn sollte dieser m¨oglichst in das
Zentrum des Fließproduktionssystems eingef¨ugt werden. Begr¨undung: Ein Pufferplatz
zerteilt das System in zwei Segmente. Je l¨anger ein Segment ist, d. h. je mehr Statio -
nen hintereinandergeschaltet sind, umso st¨arker k¨onnen sich Blockierungs- und Starving-
effekte kumulieren. Je k¨urzer ein Segment ist, umso geringer sind diese Effekte. Die Pro-
duktionsrate des Gesamtsystems wird aber offensichtlich von dem leistungschw¨achsten
Segment bestimmt. Der
Im folgenden ist ein Optimierungsprotokoll wiedergegeben, das zeigt, wie f¨ur das obige
Fließproduktionssystem beginnend mit 0 Puffern schrittweise jeweils ein zus¨atzlicher
Puffer an der bestm¨oglichen Position hinzugef¨ugt wurde.
Prod.-Rate 1 2 3 4 5
0.07572 -- 0 0 0 0
+ + + Vergr¨osserung der Puffer + + +
Puffer 3: Anstieg: 0.004694 neue Produktionsrate: 0.08042
Aktuelle Gesamtanzahl der Puffer = 1
0.08042 -- 0 1 0 0
+ + + Vergr¨osserung der Puffer + + +
Puffer 4: Anstieg: 0.004620 neue Produktionsrate: 0.08504
Aktuelle Gesamtanzahl der Puffer = 2
0.08504 -- 0 1 1 0
+ + + Vergr¨osserung der Puffer + + +
Puffer 2: Anstieg: 0.001605 neue Produktionsrate: 0.08664
Aktuelle Gesamtanzahl der Puffer = 3
0.08664 -- 1 1 1 0
+ + + Vergr¨osserung der Puffer + + +
Puffer 5: Anstieg: 0.003032 neue Produktionsrate: 0.08967
Aktuelle Gesamtanzahl der Puffer = 4
0.08967 -- 1 1 1 1
+ + + Vergr¨osserung der Puffer + + +
88

Puffer 3: Anstieg: 0.001406 neue Produktionsrate: 0.09108
Aktuelle Gesamtanzahl der Puffer = 5
0.09108 -- 1 2 1 1
+ + + Vergr¨osserung der Puffer + + +
Puffer 4: Anstieg: 0.001326 neue Produktionsrate: 0.09240
Aktuelle Gesamtanzahl der Puffer = 6
0.09240 -- 1 2 2 1
+ + + Vergr¨osserung der Puffer + + +
Puffer 3: Anstieg: 0.000510 neue Produktionsrate: 0.09291
Aktuelle Gesamtanzahl der Puffer = 7
0.09291 -- 1 3 2 1
+ + + Vergr¨osserung der Puffer + + +
Puffer 5: Anstieg: 0.000681 neue Produktionsrate: 0.09360
Aktuelle Gesamtanzahl der Puffer = 8
0.09360 -- 1 3 2 2
+ + + Vergr¨osserung der Puffer + + +
Puffer 2: Anstieg: 0.000746 neue Produktionsrate: 0.09434
Aktuelle Gesamtanzahl der Puffer = 9
0.09434 -- 2 3 2 2
+ + + Vergr¨osserung der Puffer + + +
Puffer 4: Anstieg: 0.000567 neue Produktionsrate: 0.09491
Aktuelle Gesamtanzahl der Puffer = 10
0.09491 -- 2 3 3 2
+ + + Vergr¨osserung der Puffer + + +
Puffer 3: Anstieg: 0.000300 neue Produktionsrate: 0.09521
Aktuelle Gesamtanzahl der Puffer = 11
0.09521 -- 2 4 3 2
+ + + Vergr¨osserung der Puffer + + +
Puffer 4: Anstieg: 0.000330 neue Produktionsrate: 0.09554
Aktuelle Gesamtanzahl der Puffer = 12
0.09554 -- 2 4 4 2
Man erkennt, daß die marginalen Produktionsratenzuw¨achse (Grenznutzen der
Puffer) mit zunehmender Gesamtanzahl von Puffern immer kleiner werden.
89
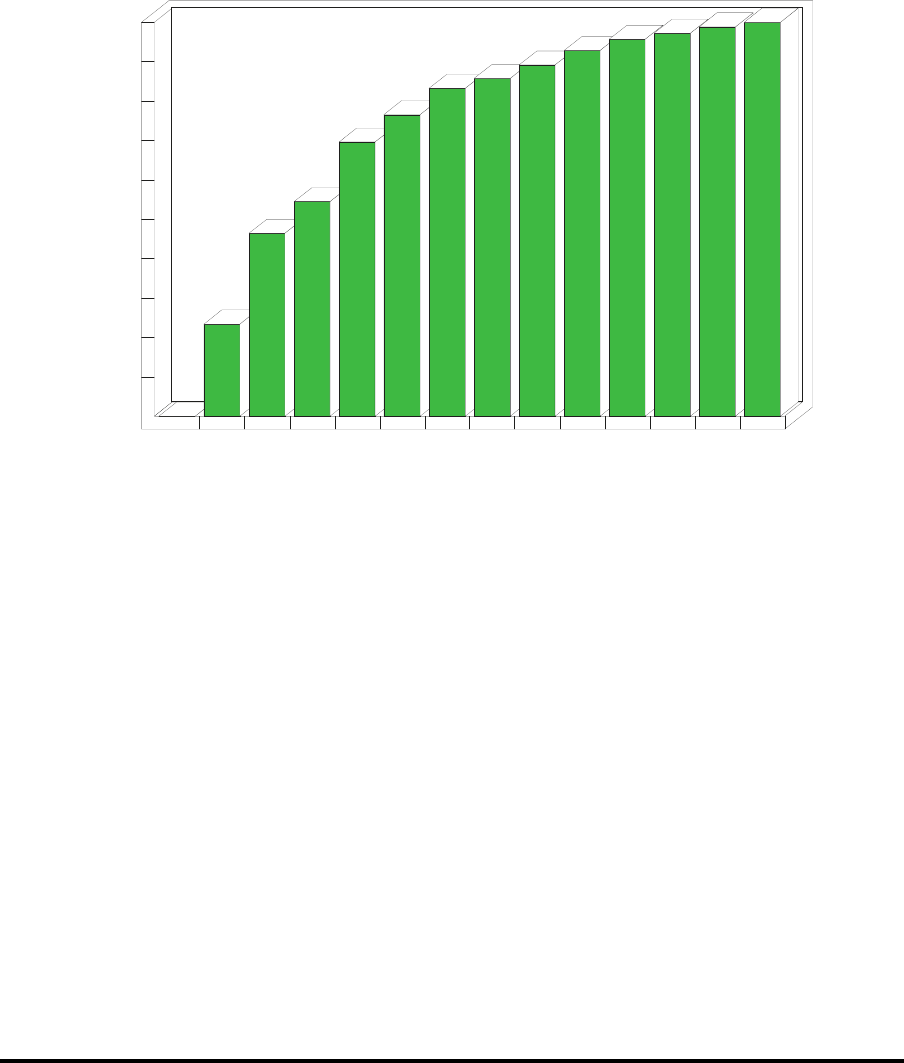
Produktionsrate
Veränderter Puffer
.07572
.07773
.07973
.08174
.08374
.08575
.08775
.08976
.09176
.09377
.09577
0 3 4 2 5 3 4 3 5 2 4 3 4 2
Die obigen Aussagen treffen allerdings nur f¨ur Systeme zu, in denen die Statio-
nen in jeder Hinsicht identisch sind. In der Praxis unterscheiden sich die Stationen
aber hinsichtlich der Bearbeitungsgeschwindigkeiten oder der St¨orparameter. In diesen
F¨allen muß man die Pufferteilung systemspezifisch ermitteln und auf die nachfolgend
behandelten Optimierungsmodelle zur¨uckgr eifen.
15.3 Optimierungsmodelle
Literaturhinweis
Tempelmeier (2018), Aufgabe A3.15
In einem Zwei-Stationen-System haben wir nur eine Entscheidungsvariable, und zwar
die Gr¨oße des einzigen Puffers. Diese kann man solange ver¨andern, bis die gew¨unschte
Produktionsrate erreicht ist. Denn die Produktionsrate ist eine konkave Funktion der
Puffergr¨oße.
So eindeutig ist die Situation bei mehr als einem Pufferbereich nicht mehr. Dies zeigt
das folgende Bild, in dem ein FPS mit drei Stationen betrachtet wird. Es wurden alle
Kombinationsm¨oglichkeiten von 0 bis 10 Puffern auf die beiden Pufferpl¨atze ausgewertet.
3-Stationen-System
Produktionsrate versus Anzahl Puffer
90
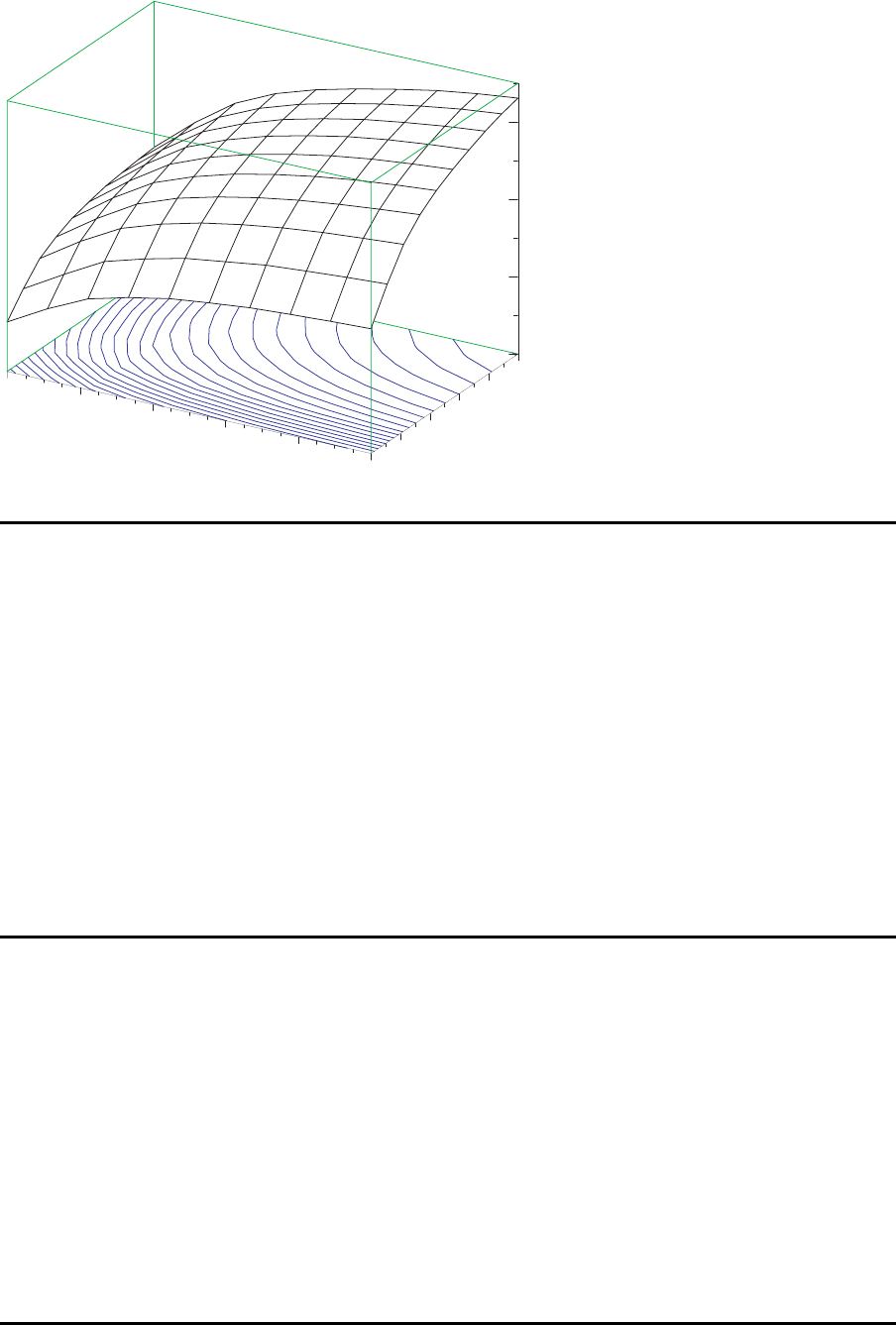
0
1
2
3
4
5
Puffer vor Station 2
1
2
3
4
5
Puffer vor Station 3
0.5
0.6
0.7
0.8
Produktionsrate
Primalproblem
Minimiere B =
N
X
n=1
b
n
u. B. d. R.
X(b
1
, b
2
, . . . , b
N
) ≥ X
Ziel
Gesucht: Minimale Gesamtanzahl von Pufferpl¨at zen bei gegebener Zielproduktionsrate
X
Ziel
Dualproblem
Maximiere Z = X(b
1
, b
2
, . . . , b
N
)
u. B. d. R.
N
X
n=1
b
n
= B
Gesucht: Optimale Verteilung einer gegebenen Anzahl von B Pufferpl¨atzen auf die Puffer
91
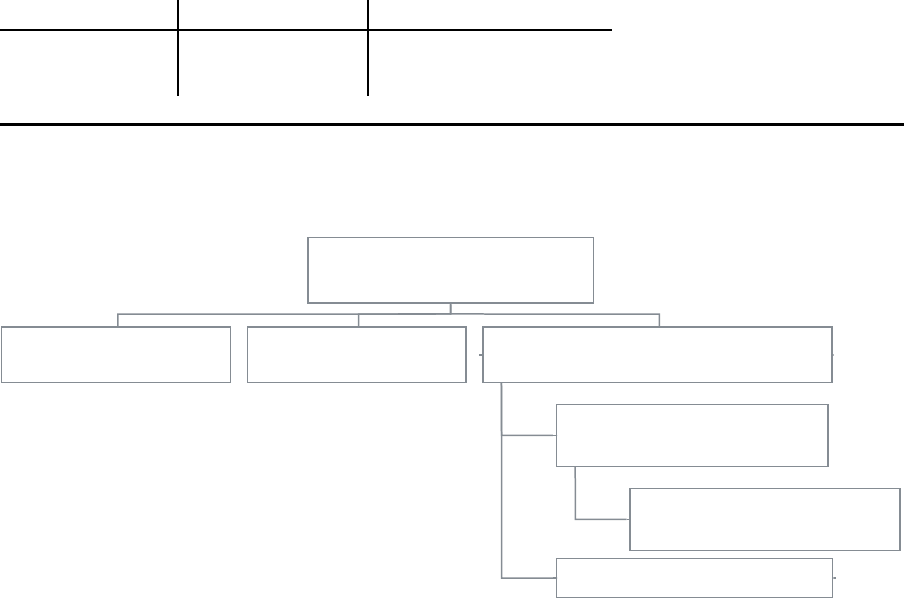
Primalproblem – Dualproblem
Gegeben Gesucht
Primalproblem Produktionsrate Mindestanzahl Puffer
Dualproblem Anzahl Puffer Verteilung der Puffer
Pufferoptimierung
L¨osungsm ethoden
Pufferoptimierung
Greedy-Verfahren Meta-Heuristiken Lösung des Primal-Problems
Iterative Approximation der
Produktionsfunktion
Lösung des Dualproblems
Gradientenverfahren
Finde optimale Pufferanzahl
Alle O ptimierungsmethoden ben¨ot igen zur Evaluation einer L¨osungsalternative ein Ver-
fahren zur Leistungsanalyse, z. B. ein Dekompositionsverfahren (siehe oben).
15.4 L¨osung des Dualproblems
Wenn wir das Dualproblem l¨osen wollen, dann k¨onnen wir von einer gegebenen
Pufferkonfiguration mit N Puffern und den Puffergr¨oßen b
1
, b
2
, . . . , b
N
ausgehen und
versuchen, diese zu verbessern. Allerdings stellt sich die Frage, welche Puffer unter der
Bedingung einer konstanten Gesamtpufferzahl B =
P
N
n=1
b
n
vergr¨o ßert und welche
verkleinert werden sollen, damit eine Verbesserung der Produktionsrate erreicht wird.
Ziel ist es ja, die Produktionsrate zu maximieren.
Einen Hinweis dar auf, welchen Beitrag ein Puffer zur Erh¨ohung der Produktionsrate
liefert, bietet der Gradient (Vektor der partiellen Ableitungen). D a wir keine geschlosse-
nen, stetig differenzierbaren Funktionen betrachten, sondern nur in der Lage sind, die
Produktionsrate als Funktion der Pufferko nfig uration an einzelnen Punkten auszuwerten,
kann man versuchen, den Gradienten g, also den Vektor der partiellen Ableitungen, zu
approximieren. Der Gradient gibt dann an, um wieviel die Produktionsrate ansteigt,
wenn man die einzelnen Puffer isoliert betrachtet marginal vergr¨oßert. Man k¨o nnte z. B.
den Puffer n isoliert um einen geringen Betrag vergr¨oßern und den resultierenden Anstieg
der Produktionsrate als Approximation der partiellen Ableitung der Produktionsrate
bez¨uglich der Variablen b
n
verwenden. Zur Berechnung der jeweiligen Produktionsrate
kann z. B. das obige Dekompositionsverfahren eingesetzt werden.
92

Bildet man aus allen Elementen des Gradienten den Mittelwert, dann kann man f¨ur
jeden Puffer die Abweichung der partiellen Ableitung vom gemeinsamen Mit-
telwert errechnen. Diese Abweichungen k¨onnen positiv oder auch negat iv sein. D. h.
die Vergr¨oßerung einiger Puffer f¨uhrt zu einem ¨uberdurchschnittlichen Produktionsra-
tenanstieg, w¨ahrend die Vergr¨oßerung anderer Puffer nur einen unterdurchschnittlichen
Anstieg der Produktionsrate bringt.
Multipliziert man diesen projizierten Gradienten mit einem beliebigen Faktor und
addiert man den resultierenden Vektor zu dem Vektor der Puffergr¨oßen, dann bleibt die
gesamte Pufferzahl konstant. Nur die Verteilung ¨andert sich.
Das folgende Bild zeigt f¨ur ein Fließproduktionssystem mit 10 Stationen (N = 9 Puffer)
die projizierten Gradienten f¨ur eine gegebene (nicht-optimale) Pufferverteilung. Zur
Bestimmung der ma r ginalen Produktionsratenver¨anderungen wurde jeder Puffer um 0.1
vergr¨o ßert. Der Berechnungen wurden mit einem Evaluationsverfahren durchgef¨uhrt, bei
dem die Puffergr¨oßen auch nicht -ganzzahlig sein d¨urfen.
Projizierter Gradient
2
3
4
5
6
7
8
9
10
Veränderung der Puffer
Verkleinerung Vergrößerung
Die Produktionsrate verl¨auft wie auf dem folgenden Bild dargestellt (hier wurde ein F PS
mit 3 Stationen betrachtet.)
93
Produktionsrate
versus Pufferverteilung
0.470
0.472
0.474
0.476
0.478
0.480
0.482
0.484
0.486
0.488
Produktionsrate
4/4 3/5 2/6 1/7 0/8
Pufferverteilung
(vor Station 2/vor Station 3)
N ist die Anzahl der Pufferbereiche (hier N = 2). g
n
ist ein Element des Gradienten an
der Stelle n. Dann erhalten wir:
Projizierter Gradient
p
n
= g
n
−
N
P
i=1
g
i
N
n = 1, 2, . . . , N
Man kann die optimale (produktionsratenmaximale) Pufferverteilung finden, indem man
die aktuelle Projektion mit einem Faktor α multipliziert und zu der a ktuellen Puffer-
konfiguration hinzuaddiert. Allerdings m¨ussen die Absch¨atzungen des Gradienten u. U.
mehrfach aktualisiert werden, da die Steigung der nichtlinearen Zielfunktion an der
jeweils aktuellen Pufferverteilung sich ¨andert und der zuletzt berechnete Gradient
nur einen ungenauen Hinweis ¨uber die Steigung der Zielfunktion an den weiter entfernten
Stellen gibt.
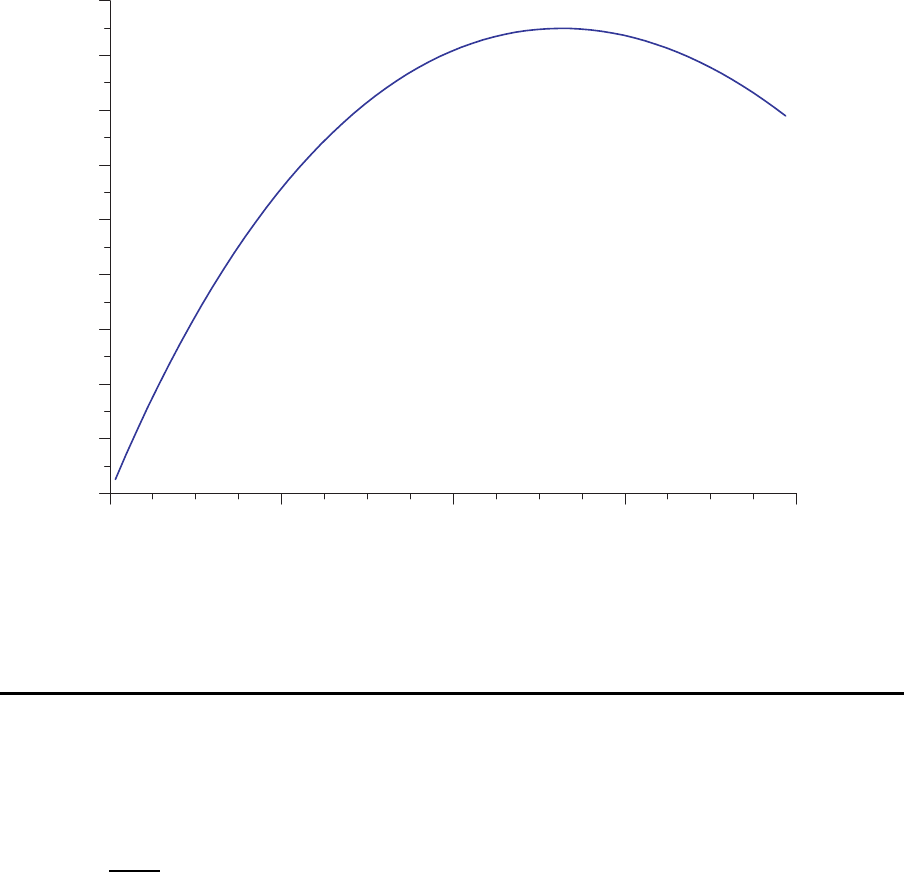
Zur weiteren Verdeutlichung der Problemstellung b etrachten wir ein Beispiel mit drei
Stationen und zwei Puffern mit insgesamt 8 Pufferpl¨atzen. Das folgende Bild zeigt
die Entwicklung der Produktionsrate, wenn man – ausgehend von einer Verteilung 4/4
(d. h. 4 Puffer vor Station 2 und 4 Puffer vor Station 3) – Pufferpl¨atze von Station 2
zur Station 3 hin verschiebt. F¨ur gr¨oßere bzw. andere Systeme sieht die Entwicklung der
94
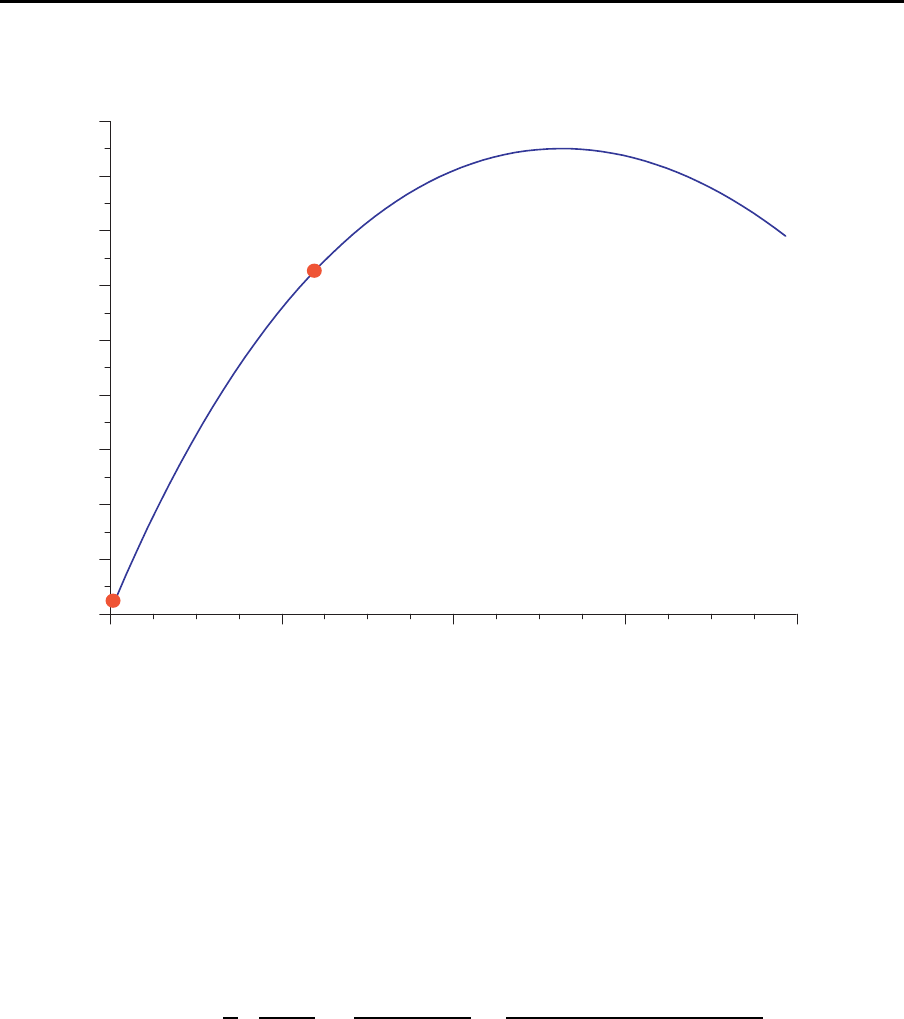
Produktionsrate ¨ahnlich aus. Man ka nn aber davon ausgehen, daß der Verlauf konkav
ist. Dies wurde zwa r nicht allgemein bewiesen, ist aber plausibel. F¨ur alle Punkte auf
der Kurve betr¨agt die Gesamtpufferanzahl 8.
Ver¨anderung der Pufferverteilung
Variation vo n α
0.470
0.472
0.474
0.476
0.478
0.480
0.482
0.484
0.486
0.488
Produktionsrate
4/4 3/5 2/6 1/7 0/8
Pufferverteilung
(vor Station 2/vor Station 3)
l=0 (Start)
l=1
aktuelle
Lösung
Wie findet man nun das Maximum dieser Funktion, ohne eine zeitaufwendige
Vollenumeration aller Pufferkombinationen durchzuf¨uhren?
Nimmt man an, daß die Puffergr¨oßen ganzzahlig sind, dann ist die Anzahl Pufferverteilun-
gen gleich der Anzahl von M¨oglichkeiten, B Element e (Puffer) zu N Gruppen (Puffer-
bereiche) zusammenzufassen. Diese Anzahl ist gegeben durch den Binomialkoeffizienten
B + N − 1
N − 1
.
Dieser ist wie folgt definiert
n
k
=
n
1
·
n − 1
2
···
n − (k − 1)
k
=
n · (n − 1) ···(n − k + 1)
k!
95

Setzen wir n = B + N − 1 und k = N − 1, dann erhalten wir
(B + N − 1) · (B + N − 2) ···(B + N − 1 − N + 1 + 1)
(N − 1)!
bzw.
(B + N − 1) · (B + N − 2) ···(B + 1)
(N − 1)!
m¨ogliche Pufferverteilungen.
Im Beispiel mit B = 8 und N = 2 erhalten wir
(8 + 1)
1
= 9
In der Graphik haben wir bereits 5 M¨oglichkeiten aufgez¨ahlt. Hinzu kommen noch die
nicht dargestellten K onfigurationen (8/0), (7/1), (6/2) und (5/3), die zu den dargestellten
Kombinationen symmetrisch sind.
Ein Verfahren, das mit den o. g. Gradient en arbeitet, sieht wie folgt aus:
1. Ausgangspunkt ist eine Startl¨osung, d. h. eine gegebene Pufferverteilung
B = (b
1
, b
2
, . . . , b
N
). Eine M¨oglichkeit besteht dar in, die Puffer gleichm¨aßig
zu verteilen.
2. Man berechnet den Gradienten g an dieser Stelle. Dabei geht man von
kontinuierlich variierbaren Puffern aus.
3. Man bestimmt dann folgende Projektion des Gradient en:
p
n
= g
n
−
N
P
i=1
g
i
N
n = 1, 2, . . . , N
Einige der p
n
-Werte sind negativ und einige sind positiv. Multipliziert
man den Vektor p mit einer Konstanten α, und addiert man das Produkt zu
der aktuellen Pufferkonfiguration, dann entspricht das einer Umverteilung
der Puffer bei konstant er Gesamtanzahl B.
Wir haben es daher nur noch mit einem nichtlinearen Maximierungsproblem mit einer
Entscheidungsvariablen α zu tun.
Dabei muß allerdings ber¨ucksichtigt werden, daß durch die Ver¨anderung der Puffergr¨oßen
kein Puffer negativ wird. Die schrittweise Verlagerung der Puffergr¨oßen a ls Funktion der
Entscheidungsvariablen α bei konstanter Gesamtanzahl der Puffer ist in den folgenden
Bildern dargestellt. Dabei wurde ausgehend von einem Startwert f¨ur α dieser schrittweise
jeweils verdoppelt.
96
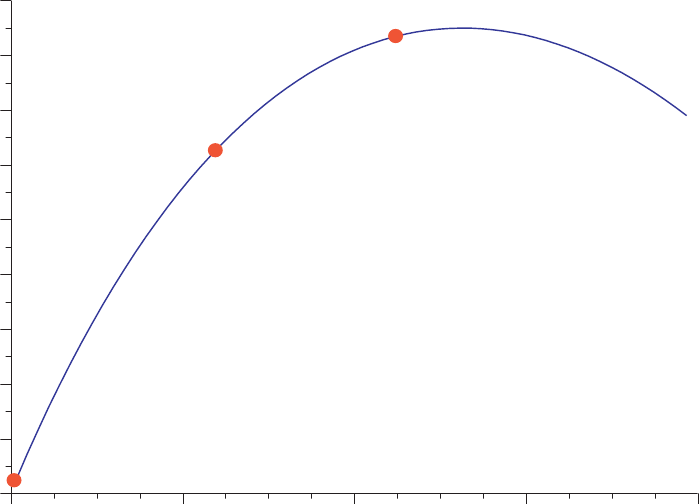
Ver¨anderung der Pufferverteilung
Variation vo n α, I teratione n ℓ = 0, 1, 2
0.470
0.472
0.474
0.476
0.478
0.480
0.482
0.484
0.486
0.488
Produktionsrate
4/4 3/5 2/6 1/7 0/8
Pufferverteilung
(vor Station 2/vor Station 3)
l=0 (Start)
l=1
aktuelle
Lösung
l=2
nächste
Lösung
97
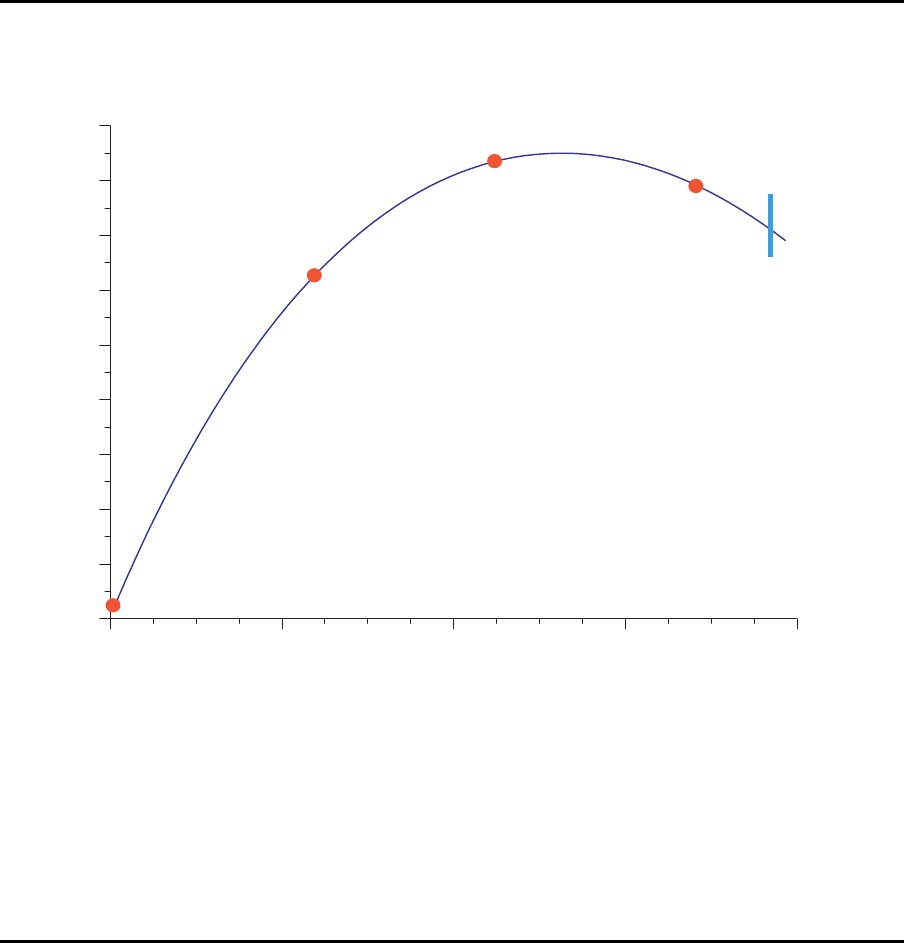
In der n¨achsten Iteration ℓ = 3 wird die Grenze α
max
immer no ch nicht erreicht, aber
die Pr oduktionsrate steigt nicht mehr an, sondern sie sinkt. Die Fr age ist nun: Wo
liegt das gesuchte Maximum? Da die Zielfunktion konkav ist, also nur ein Maximum
hat, muß der gesuchte Punkt im Bereich zwischen ℓ = 1 und ℓ = 3 liegen.
Ver¨anderung der Pufferverteilung
Variation vo n α, ℓ = 3
0.470
0.472
0.474
0.476
0.478
0.480
0.482
0.484
0.486
0.488
Produktionsrate
4/4 3/5 2/6 1/7 0/8
Pufferverteilung
(vor Station 2/vor Station 3)
l=0 (Start)
l=1
l=2
aktuelle
Lösung
l=3
nächste
Lösung
max
Warum liegt der linke Rand des Suchbereichs bei ℓ = 1 und nicht bei ℓ = 2?
Aus dem obigen Bild kann man doch sehen, daß das Maximum der Funktion rechts von
ℓ = 2 liegt.
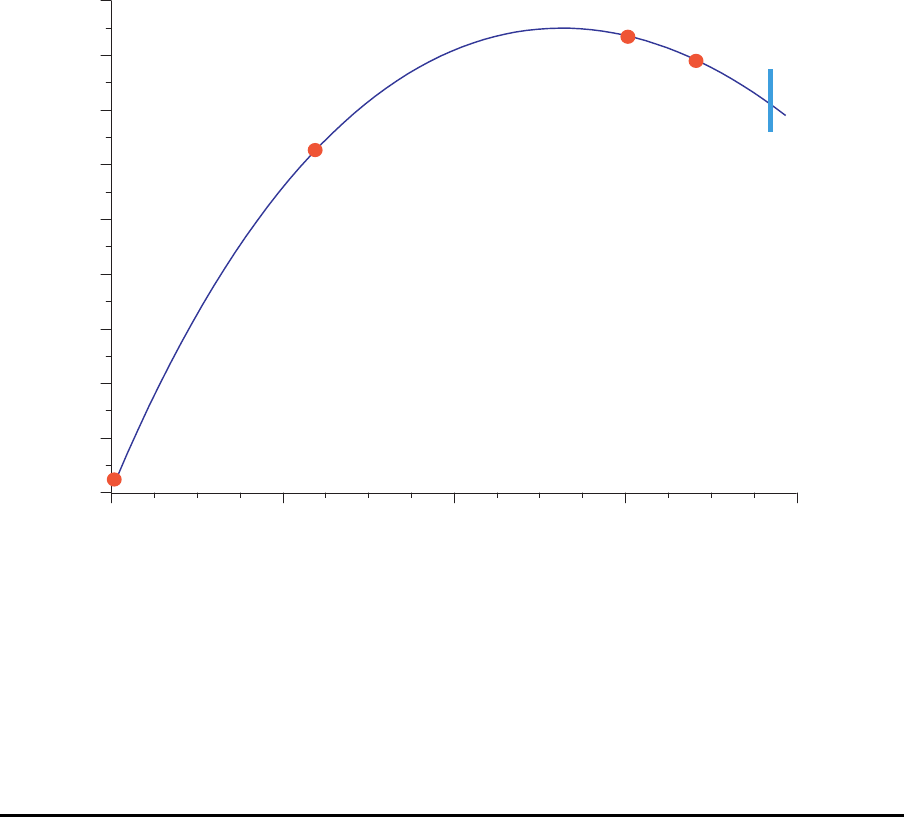
Um diese Frage zu beantworten, betrachten wir den im folgenden Bild dargestellten Ver-
lauf der Funktion, in dem bereits der Versuch ℓ = 2 rechts vom Maximum und damit das
Maximum zwischen ℓ = 1 und ℓ = 2 liegt.
Ver¨anderung der Pufferverteilung
Anderer Verlauf der Funktion der Produktionsrate
98
0.470
0.472
0.474
0.476
0.478
0.480
0.482
0.484
0.486
0.488
Produktionsrate
4/4 3/5 2/6 1/7 0/8
Pufferverteilung
(vor Station 2/vor Station 3)
l=0 (Start)
l=1
l=2
aktuelle
Lösung
l=3
nächste
Lösung
max
Hier w¨are der Suchprozess genauso verlaufen wie zuvor angenommen. Nur liegt das
tats¨achliche Maximum links von dem Punkt ℓ = 2. Dies kann aber nicht erkannt
werden, da man die Produktionsrate ja nur an den mit den Punkten markierten Stellen
berechnet. Daher wissen wir, daß im Beispiel das gesucht e Maximum im Bereich zwischen
α
1
und α
3
liegt. Falls der Punkt f¨ur α
3
rechts von α
max
liegt, dann liegt das Maximum
zwischen α
1
und α
max
. Da s zeigt das folgende Bild.
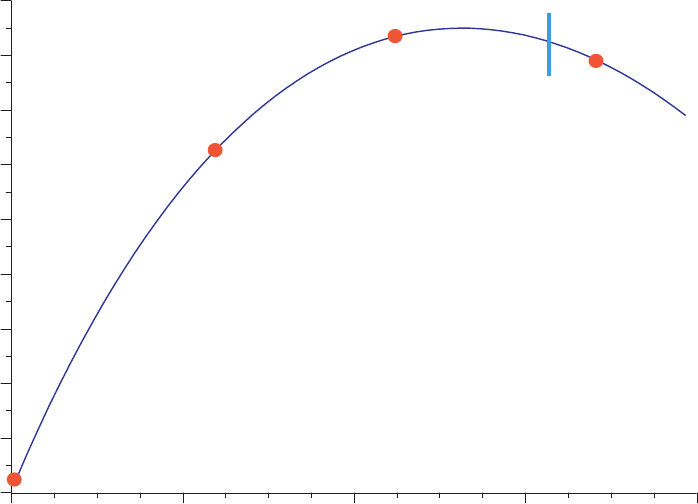
Ver¨anderung der Pufferverteilung
Variation vo n α
99
0.470
0.472
0.474
0.476
0.478
0.480
0.482
0.484
0.486
0.488
Produktionsrate
4/4 3/5 2/6 1/7 0/8
Pufferverteilung
(vor Station 2/vor Station 3)
l=0 (Start)
l=1
l=2
aktuelle
Lösung
l=3
nächste
Lösung
max
Die Berechnung des aktuellen Suchbereichs basiert auf dem aktuellen Gradienten
an der Stelle ℓ = 0 mit der Produktionsrate X
0
und den Puffergr¨oßen b
0
. Die Suche ¨uber
diesen Bereich wird abgebrochen,
1. wenn ein neuer Punkt α
ℓ
¨uber α
max
hinausreicht
2. wenn die Produktionsrate wieder sinkt oder nicht mehr ansteigt, d. h. X
ℓ
≤ X
ℓ−1
Zur genauen Bestimmung des Maximums der Funktion (bzw. des optimalen Werts von
α) kann z. B. das Verfahren des Goldenen Schnitts eingesetzt werden. Nach der Be-
stimmung des optimalen Werts von α wird das bisher beschriebene Verfahren wiederholt,
d. h. es wird ein neuer Gradient berechnet, etc. Dies wird solange fortgesetzt, bis die
einzelnen Elemente des Gradient ann¨ahernd gleich sind, so daß durch eine Ver¨anderung
des Pufferverteilung keine weitere Erh¨ohung der Produktionsrate erreicht werden kann.
Wir betracht en jetzt ein Beispiel, wobei deterministische Bearbeitungszeiten und Maschi-
nenausf¨a lle angenommen werden. Die numerischen Berechnungen der Produktionsraten
der verschiedenen Systemkonfigurationen k¨onnen nicht mit dem obigen Dekompositionsver-
fahren nachvollzog en werden, da dort exponentialverteilte Bearbeitungszeiten und keine
Maschinenausf¨alle unterstellt wurden. D a wir uns jetzt auf das Verfahren zur L¨osung
des Dualproblems konzentrieren, gehen wir einfach davon an, daß wir in der Lage sind,
die Produktionsrate f¨ur jede Systemkonfiguration auszurechnen. Prinzipiell k¨onnte man
auch ein Simulationsmodell einsetzen. Das w¨urde allerdings wegen der langen Laufzeiten
zuviel Zeit in Anspruch nehmen.
100
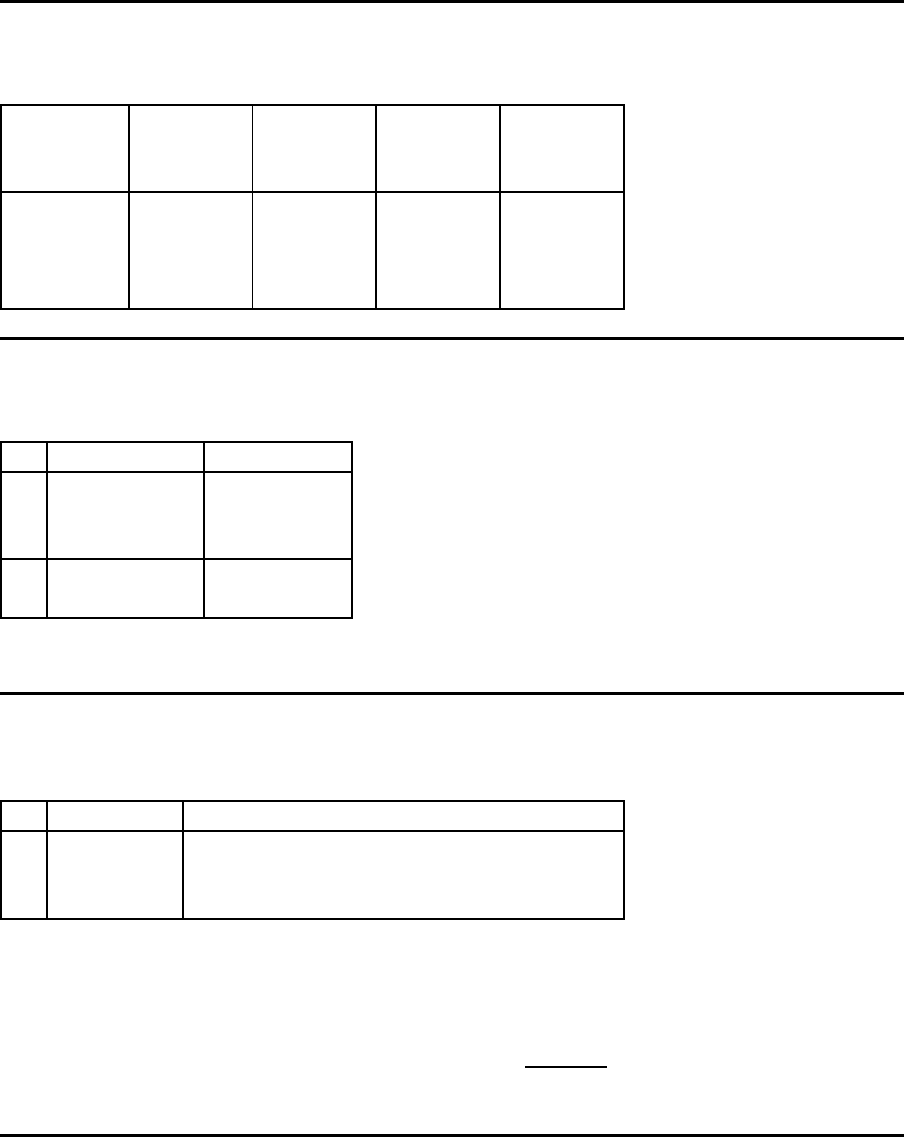
Beispiel
Daten
Station m Puffer-
gr¨oße
Bearbei-
tungsrate
Ausfall-
rate
Reparatur-
rate
1 – 1.000000 0.1 1.000000
2 0 1.000000 0.1 1.000000
3 6 1.000000 0.1 1.000000
4 4 1.000000 0.1 1.000000
Beispiel
Grad i ent
m Puffer g
m
2 0.0 0.00328809
3 6.0 0.00017786
4 4.0 0.00008243
Summe 0.00354838
Durchschnitt 0.001182793
Der Wert g
1
ergibt sich als X(0.1, 6, 4) − X(0, 6, 4 ) . g
2
= X(0, 6.1, 4) − X(0, 6, 4), usw.
Beispiel
Berechnung der Projektion des Gradienten
m g
m
p
m
2 0.00328809 0.00328809 – 0.001182793 = 0.00210530
3 0.00017786 0.00017786 – 0.00118279 3 = -0.00100493
4 0.00008243 0.00008243 – 0.00118279 3 = -0.00110036
Man kann nun eines der bekannten Verfahren zur Maximierung einer nichtlinearen Funk-
tion einer unabh¨angigen Variablen (hier α ) einsetzen. Um den Suchbereich einzugrenzen,
kann man - ausgehend von einem kleinen Startwert - α iterativ solang verdoppeln, bis
der Funktionswert (d. h. die Produktionsrate) wieder sinkt.
Im vorliegenden Beispiel wird ein Startwert α =
1
0.00210530
= 474.99244 festgelegt und
dieser dann in jeder Iteration verdoppelt. Andere Vorgehensweisen sind m¨oglich.
Beispiel
Neue Puffe rv erteilung
b
ℓ
= b
0
+ α
ℓ
·p
101
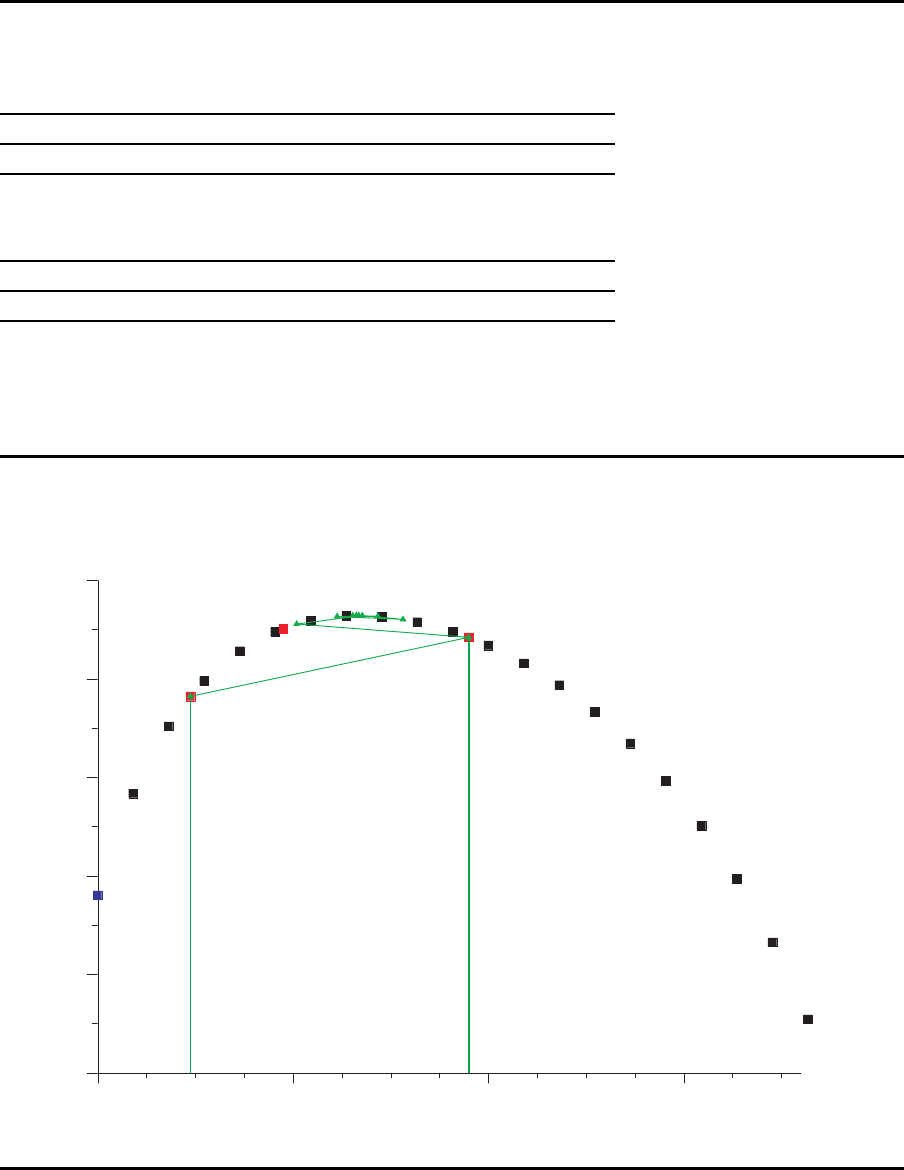
Durch die Addition des α
ℓ
-fachen der Projektion des Gradienten zu den aktellen Puffern
¨andert sich die Gesamtanzahl der Pufferpl¨atze nicht, da die Summe der Elemente des
Vektors p gleich 0 ist.
Beispiel
Pufferverteilungen (Zwischenergebnisse)
Iteration ℓ 1 2 3
α
ℓ
474.99244 949.98488 1899.96976
m 2 1.00000 2.00000 4.00000
3 5.52266 5.04533 4.09066
4 3.47734 2.95467 1.90934
X 0.8482202 0.855 1133 0.8542113
Summe 10 10 10
Nach dem ersten Verfahrensschritt kann man dann die Suche weiter verfeinern. Das
folgende Bild zeigt die Ergebnisse, wenn man α mit dem Verfahren des Goldenen
Schnitt es (Golden-Section-Search) ermittelt.
Beispiel
Zielfunktionsverlauf
0.81
0.82
0.83
0.84
0.85
0.86
Produktionsrate
0 1000 2000 3000
α
1
2
3
4
5
6
7
8
9
l=1
l=2
l=3
102
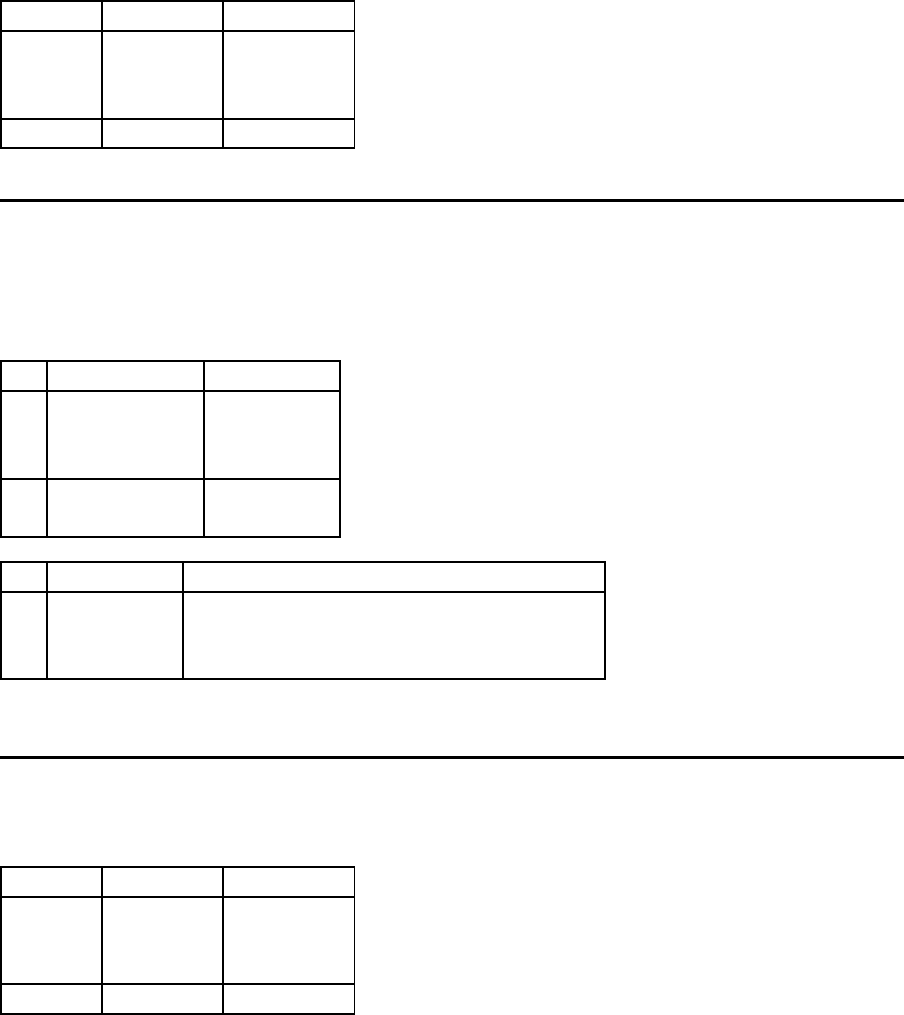
Beispiel
L¨osung nach Abschluß der Dual-Iteration 1
Die aktuelle Pufferkonfiguration sieht wie folg t aus:
m Puffer alt Puffer neu
2 0 2.85400
3 6 4.63768
4 4 2.50832
Summe 10 10
Beispiel
Beginn der Dual-Iteration 2
Jetzt berechnet man den Gradienten an der Stelle der neuen Pufferkonfiguration:
m Puffer g
m
2 2.85400 0.00038117
3 4.63768 0.00030982
4 2.50832 0.00047565
Summe 0.00116664
Durchschnitt 0.00038888
m g
m
p
m
2 0.00038117 0.00038117 – 0.0003888 = –0.00000771
3 0.00030982 0.00030982 – 0.0003888 = –0.00007906
4 0.00047565 0.00047565 – 0.0003888 = 0.00008677
usw. (siehe oben)
Beispiel
L¨osung nach Abschluß der Dual-Iteration 2
m Puffer alt Puffer neu
2 2.85400 2.82807
3 4.63768 4.37177
4 2.50832 2.80016
Summe 10 10
Diese L¨osung l¨aßt sich nicht mehr verbessern. Daher wird das Verfahren zur L¨osung des
Dualproblems beendet.
Nach Auf- bzw. Abrunden ist die optimale Pufferverteilung b
1
= 3, b
2
= 4, b
3
= 3.
Fazit: Man hat das Problem in ein nichtlineares Optimierungsproblem mit einer Vari-
ablen transformiert und kann dann im Prinzip ein beliebiges Suchverfahren einsetzen.
103

Bei jeder Ver¨anderung der Pufferverteilung muß man dann jeweils die Produktionsrate
bestimmen. Hierzu setzt man z. B. ein Dekompositionsverfahren ein.
L¨osung des Dualproblems
Es folgen weitere Dual-Iterationen mit folgenden Schritten:
1. Gradienten f¨ur die neue Pufferkonfiguration berechnen und pr¨ufen, ob die g
n
-Werte
ann¨ahernd gleich sind.
Wenn ja, evtl. Puffer auf ganzzahlige Werte runden und STOP. Wenn nein:
• Projektion berechnen
• α variieren und Puffer verschieben
2. Gehe zu Schritt 1.
Damit ist die optimale Pufferverteilung f¨ur eine gegebene Gesamtanzahl von Pufferpl¨atzen
gefunden. Diesem Dualproblem ¨ubergeordnet ist das Primalproblem, dessen L¨osung
hier nicht behandelt wird.
104