7_a
14 Leistungsanalyse von gro ßen Fließproduktionssys-
temen
Aufgabe
Warum kann man l¨angere Fließproduktionssysteme i. d. R. nicht mit dem Markov-Modell
analysieren?
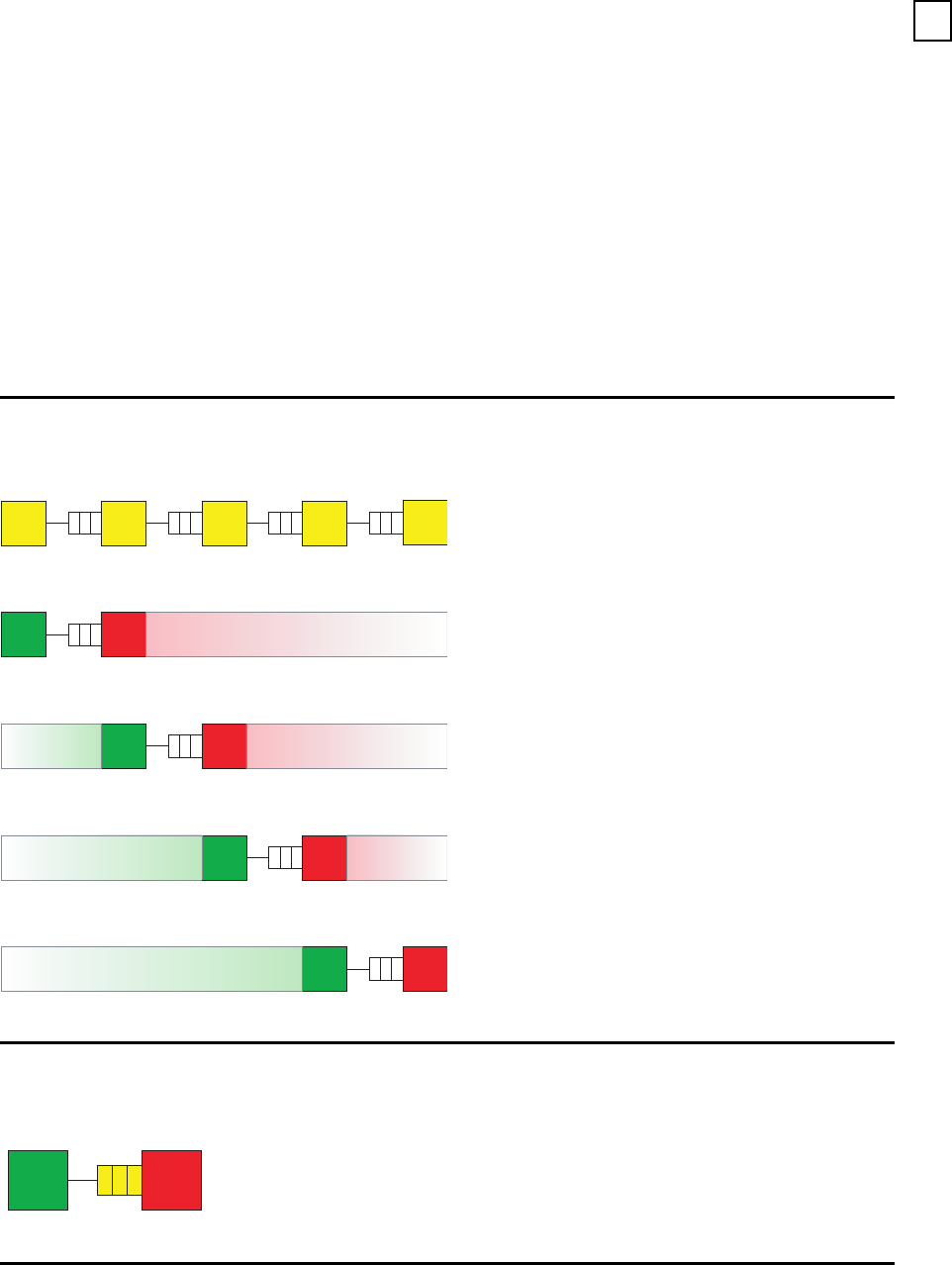
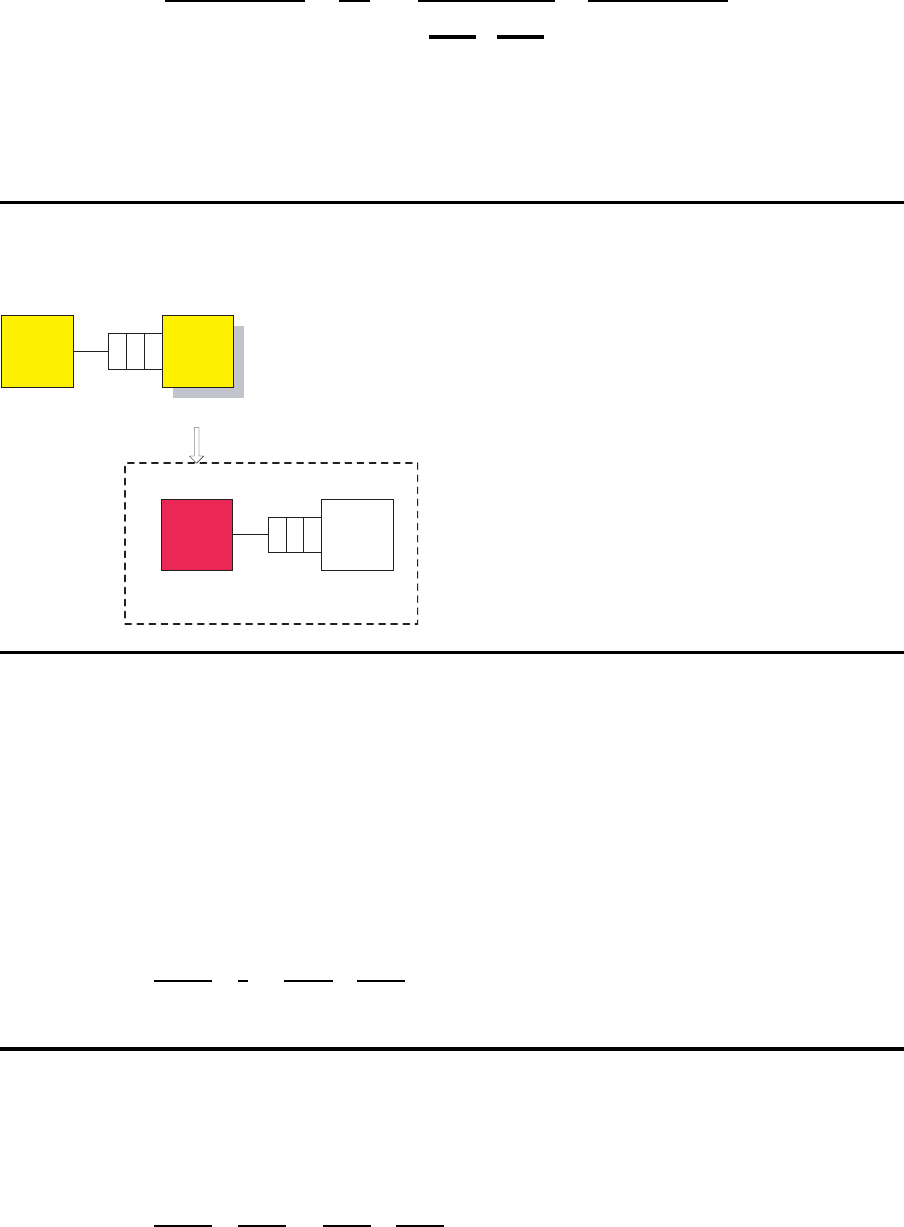
14.1 Dekomposition
Dekomposition des Fließproduktionssystems
M
1
M
2
M
3
M
4
b
1
b
2
b
3
b
4
M
u
(1,2)
b
u
(1,2) b
d
(1,2)
M
u
(2,3)
M
d
(2,3)
b
u
(2,3)
b
d
(2,3)
M
u
(3,4) M
d
(3,4)
b
u
(3,4) b
d
(3,4)
3 421
1
2 3
3 4
B(1,2) B(2,3) B(3,4)
M
d
(1,2)
2
Subsystem (1,2)
Subsystem (2,3)
Subsystem (3,4)
M
5
b
5
5
M
u
(4,5) M
d
(4,5)
b
u
(4,5) b
d
(4,5)
4 5
Subsystem (4,5)
B(4,5)
Zwei-Stationen-Subsystem
M
u
(m,m+1)
M
d
(m,m+1)
µ
u
(m,m+1)
c
m,m+1
µ
d
(m,m+1)
m m+1
81
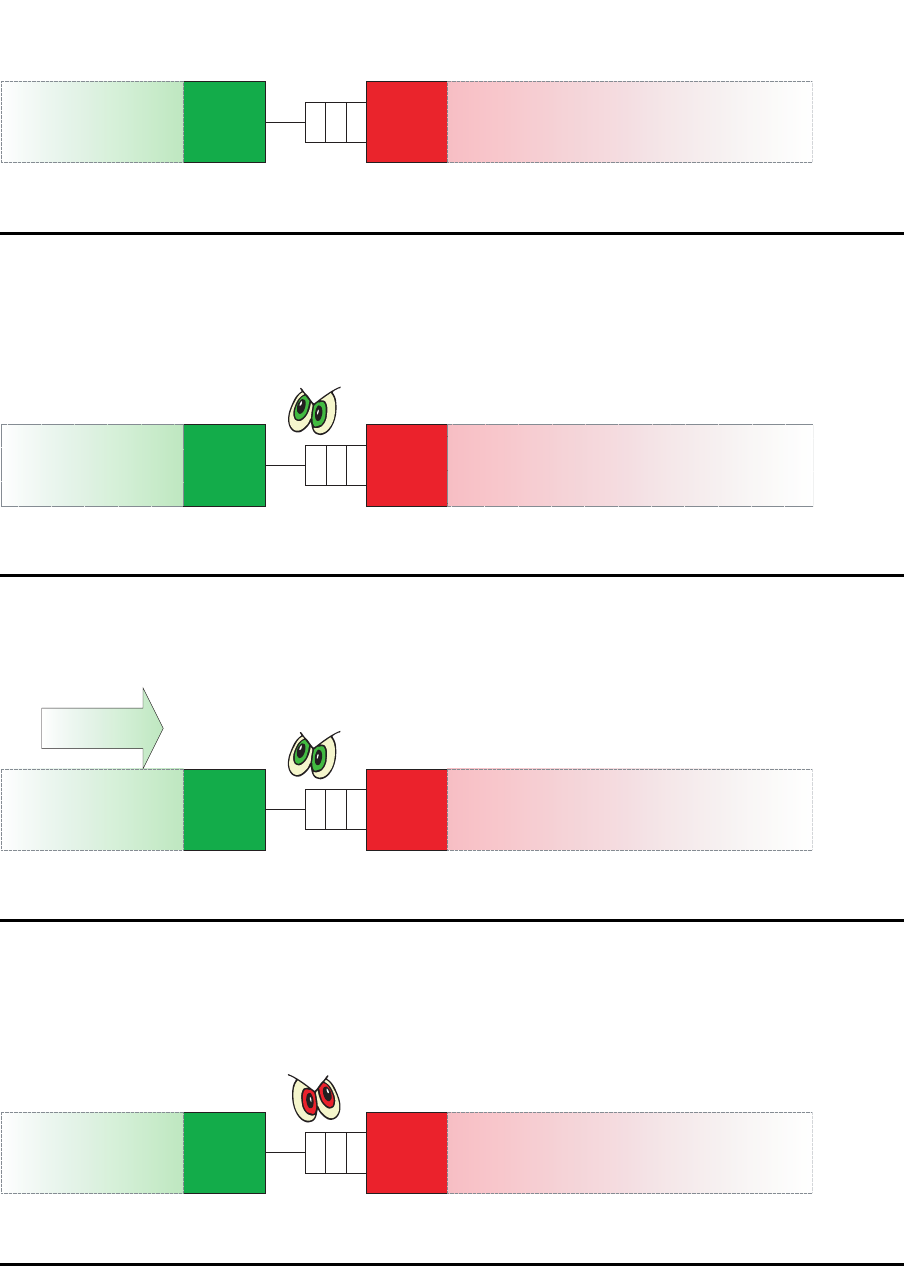
Zwei-Stationen-Subsystem
Starving
M
u
(2,3)
M
d
(2,3)
b
u
(2,3)
b
d
(2,3)
2 3
Subsystem (2,3)
Zwei-Stationen-Subsystem
Starving
M
u
(2,3)
M
d
(2,3)
b
u
(2,3)
b
d
(2,3)
2 3
Subsystem (2,3)
Zwei-Stationen-Subsystem
Starving
M
u
(2,3)
M
d
(2,3)
b
u
(2,3)
b
d
(2,3)
2 3
Subsystem (2,3)
starved
Zwei-Stationen-Subsystem
Blocking
M
u
(2,3)
M
d
(2,3)
b
u
(2,3)
b
d
(2,3)
2 3
Subsystem (2,3)
82
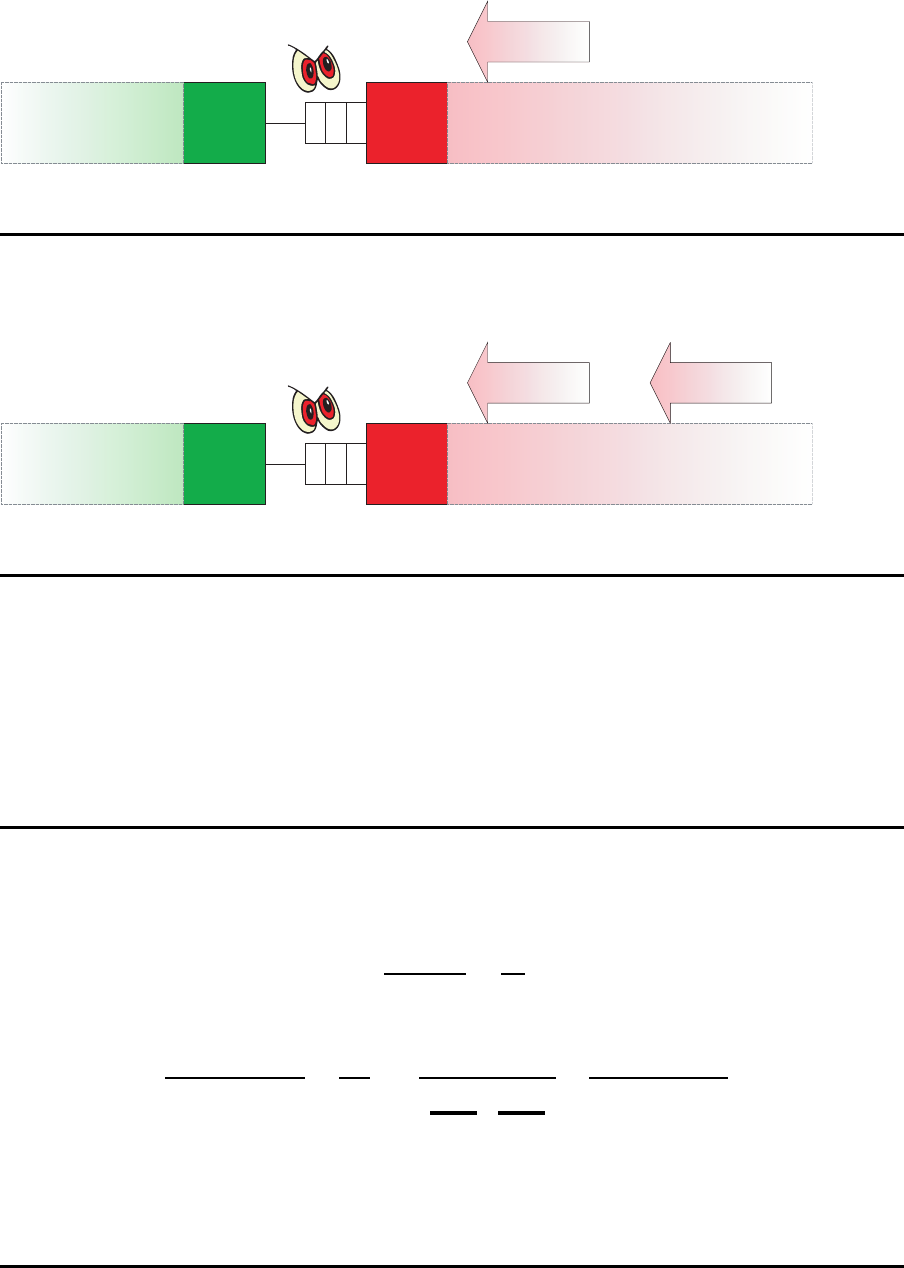
Zwei-Stationen-Subsystem
Blocking
M
u
(2,3)
M
d
(2,3)
b
u
(2,3)
b
d
(2,3)
2 3
Subsystem (2,3)
blocked
Zwei-Stationen-Subsystem
Blocking
M
u
(2,3)
M
d
(2,3)
b
u
(2,3)
b
d
(2,3)
2 3
Subsystem (2,3)
blocked blocked
Zwei-Stationen-Subsystem
• Die Rate µ
u
soll den Einfluß aller stromaufw¨arts gelegenen Stationen wiedergeben
(starving).
• Die Rate µ
d
soll den Einfluß aller stromabw¨arts gelegenen Stationen wiedergeben
(blocking).
Berechnung der µ
u
-Werte
Vorw¨artsrechnung
1
µ
u
(1, 2)
=
1
µ
1
1
µ
u
(m, m + 1)
=
1
µ
m
+
1
X (m − 1, m)
| {z }
⋆
−
1
µ
d
(m − 1, m)
m = 2, 3, ..., M −1
⋆ – dieser Wert wird mit einem 2-Stationen-Modell berechnet
83
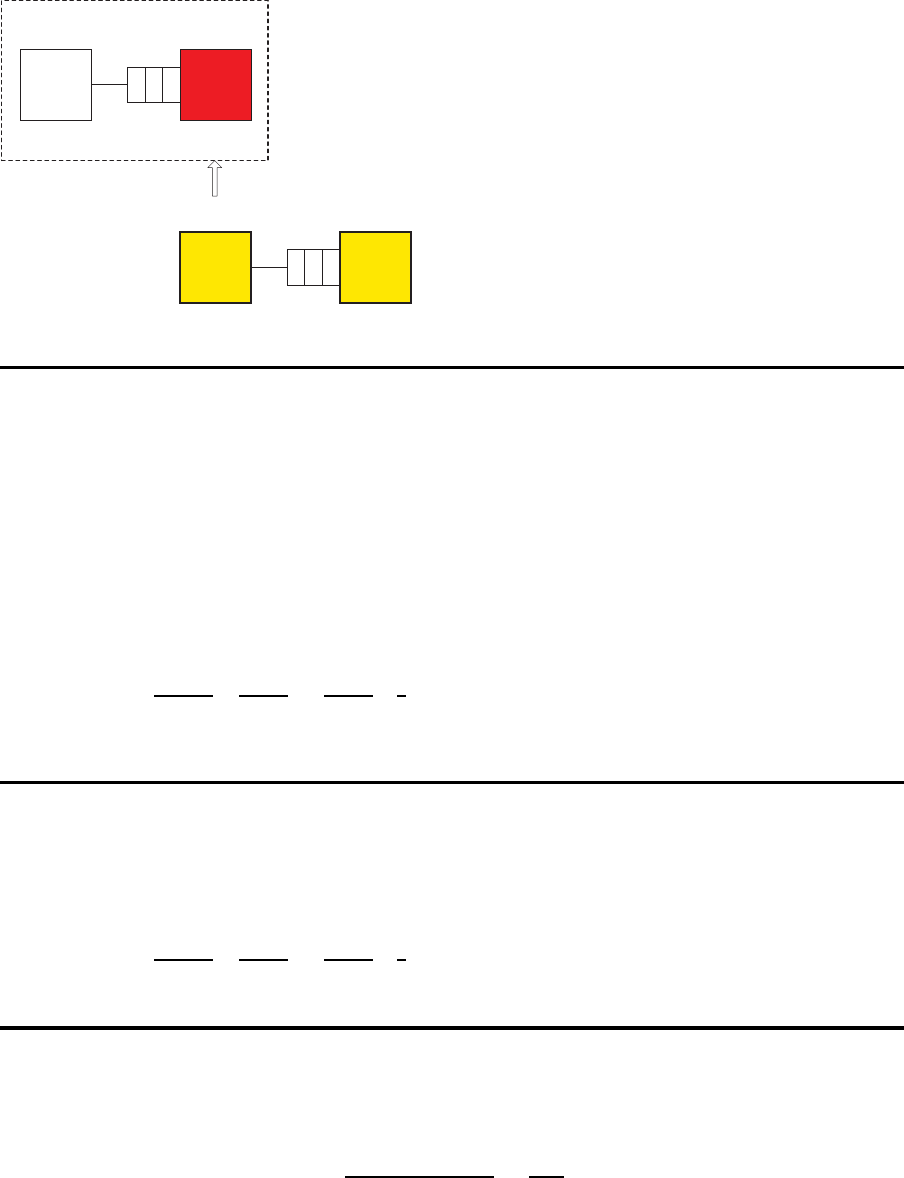
Erfassung von Starving
M
u
(m-1,m)
M
d
(m-1,m)
µ
u
(m-1,m)
c
m-1,m
µ
d
(m-1,m)
M
u
(m,m+1)
M
d
(m,m+1)
µ
u
(m,m+1)
µ
d
(m,m+1)
c
m,m+1
m-1 m
m m+1
Vorw¨artsrechnung
Iteration 1
Vorw¨artsrechnung ..............
Berechnung der Zugangsraten bei gegebenen Bedienraten
Subsystem [1,2]
Station 1 ist niemals unbesch¨aftigt!
Bedienrate der Upstream-Station M
u
(1, 2): µ
u
(1, 2) = 1.0000
Subsystem [2,3]
Berechne Produktionsrate X(1, 2)
µ
u
(1, 2) = 1.0000, µ
d
(1, 2) = 1.0000
X(1, 2) = 1.0000 · (1 − 0.3333) = 0.6667
1
µ
u
(2, 3)
=
1
1.0000
+
1
0.6667
−
1
1
= 1.5000
Bedienrate der Upstream-Station M
u
(2, 3): µ
u
(2, 3) = 0.6667
Vorw¨artsrechnung
Subsystem [3,4]
Berechne Produktionsrate X(2, 3)
µ
u
(2, 3) = 0.6667, µ
d
(2, 3) = 1.0000
X(2, 3) = 1.0000 · (1 − 0.4737) = 0.5263
1
µ
u
(3, 4)
=
1
1.0000
+
1
0.5263
−
1
1
= 1.9000
Bedienrate der Upstream-Station M
u
(3, 4): µ
u
(3, 4) = 0.5263
Berechnung der µ
d
-Werte
R¨uckw¨artsrechnung
1
µ
d
(M −1, M)
=
1
µ
M
84
1
µ
d
(m − 1, m)
=
1
µ
m
+
1
X (m, m + 1)
| {z }
⋆
−
1
µ
u
(m, m + 1)
m = M − 1, M −2, ..., 2
⋆ – dieser Wert wird mit einem 2-Stationen-Modell berechnet
Erfassung von Blocking
M
u
(m-1,m)
M
d
(m-1,m)
u(m-1,m)
c
m-1,m
d(m-1,m)
M
u
(m,m+1)
M
d
(m,m+1)
u
(m,m+1)
d
(m,m+1)
c
m,m+1
m-1 m
m m+1
µ
µ
µ
µ
R¨uckw¨artsrechnung
Iteration 1
R ¨uckw¨artsrechnung ..............
Berechnung der Bedienraten bei gegebenen Zugangsraten
Subsystem [3,4]
Station 4 ist niemals blockiert!
Bedienrate der Downstream-Station M
d
(3, 4): µ
d
(3, 4) = 1.0000
Subsystem [2,3]
Berechne Produktionsrate X(3, 4)
µ
u
(3, 4) = 0.5263, µ
d
(3, 4) = 1.0000
X(3, 4) = 1.0000 · (1 − 0.5545) = 0.4455
1
µ
d
(2, 3)
=
1
1
+
1
0.4455
−
1
0.5263
= 1.3448
Bedienrate der Downstream-Station M
d
(2, 3): µ
d
(2, 3) = 0.7436
R¨uckw¨artsrechnung
Subsystem [1,2]
Berechne Produktionsrate X(2, 3)
µ
u
(2, 3) = 0.6667, µ
d
(2, 3) = 0.7436
X(2, 3) = 0.7436 · (1 − 0.3703) = 0.4682
1
µ
d
(1, 2)
=
1
1.0000
+
1
0.4682
−
1
0.6667
= 1.6357
Bedienrate der Downstream-Station M
d
(1, 2): µ
d
(1, 2) = 0.6113
85
Hinweis
Ein Modul im Produktions-Management-Trainer demonstriert die Berechnungen.
86