6
11.3 St¨orungen, Completion Time
St¨orungsarten
• Zeitabh¨angige St¨orungen
• Operationsabh¨angige St¨orungen
Im Folgenden b etrachten wir operationsabh¨angige (nutzungsabh¨angige) St¨or ung en.
Zur Completion Time siehe:
http://www.produktion-und-logistik.de/produktionundlo gistik-485a.html
Completion Time
Verf¨ugbarkeit (isolated efficiency):
e
m
=
MT T F
m
MT T F
m
+ MT T R
m
m = 1, 2, ..., M
Mittlere st¨orungsfreie Zeit:
MT T F
m
= MT T R
m
·
e
m
1 − e
m
m = 1, 2, ..., M
Ausfallrate:
p
m
=
1
MT T F
m
m = 1, 2, ..., M
Completion Time
mittlere Reparaturzeit pro Betriebszeiteinheit:
p
m
·MT T R
m
=
MT T R
m
MT T F
m
m = 1, 2, ..., M
Reparaturzeit pro Bearbeitungsvorgang an Maschine m:
MT T R
m
MT T F
m
· b
m
m = 1, 2, ..., M
Completion time, Mittelwert:
h
m
= b
m
+
MT T R
m
MT T F
m
· b
m
m = 1, 2, ..., M
58

Completion Time
Completion time, Variationskoeffizient:
CV
2
H;m
=
CV
2
R;m
· MT T F
m
+ MT T F
m
b
m
·
1 +
MT T F
m
MT T R
m
2
+ CV
2
B;m
Man kann jetzt das Verfahren zur approximativen Leistungsanalyse des Fließpro duk-
tionssystems bei allgemein verteilten Bearbeitungszeiten (http://www.produktion-
und-logistik.de/produktionundlogistik-485.html) anwenden, wobei als Bearbeitungszeit
die Completion Time verwendet wird.
59
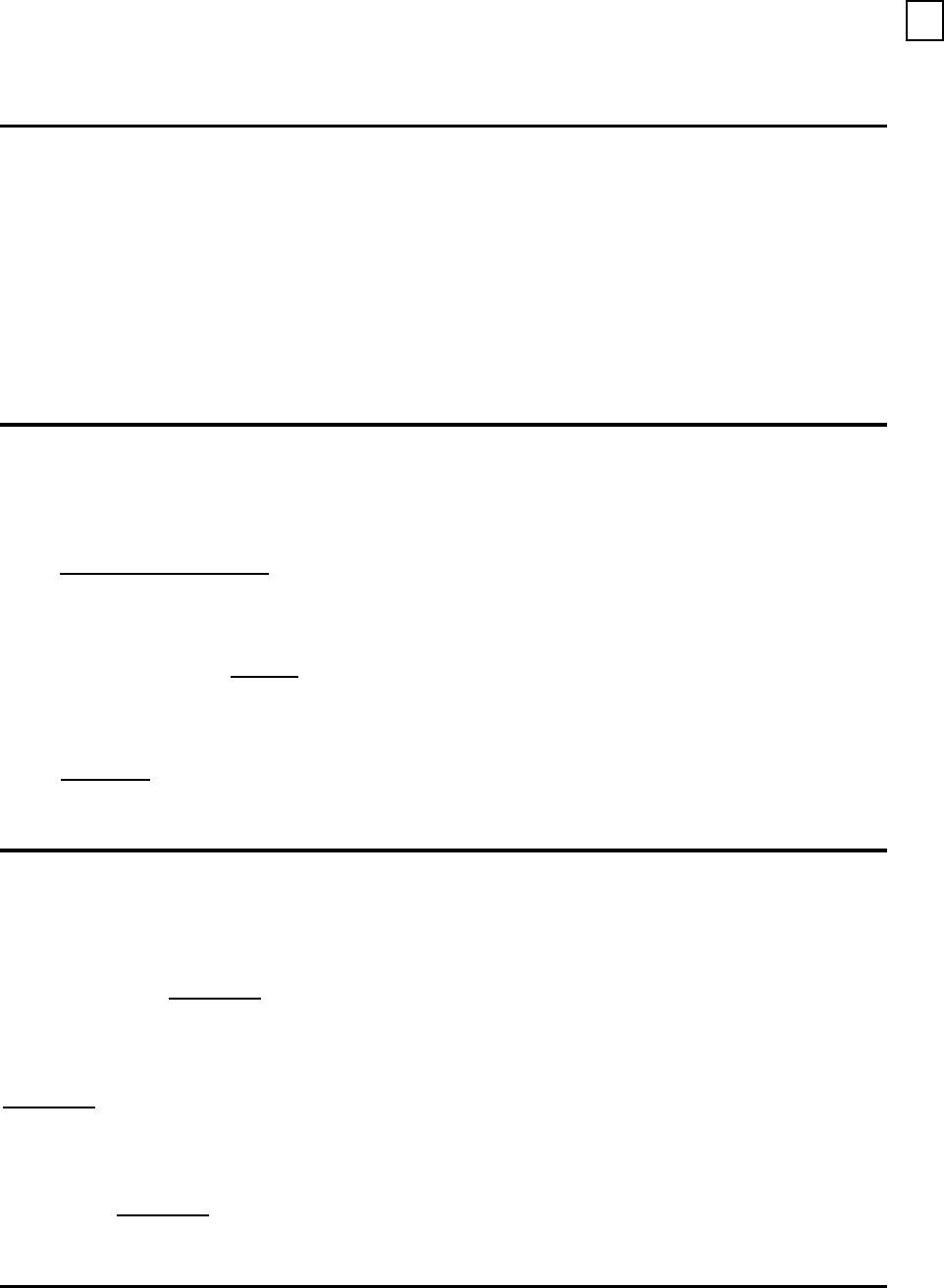
11.4 Beschr¨ankte Puffer
Blockierung
Station 1
Station 2
Station 3
Bearbeitungs-
ende: Station 2
ist blockiert
Station 3
ist voll
Sind die Puffer zwischen Stationen beschr¨ankt, dann kann es zu Blocking und Starving
kommen.
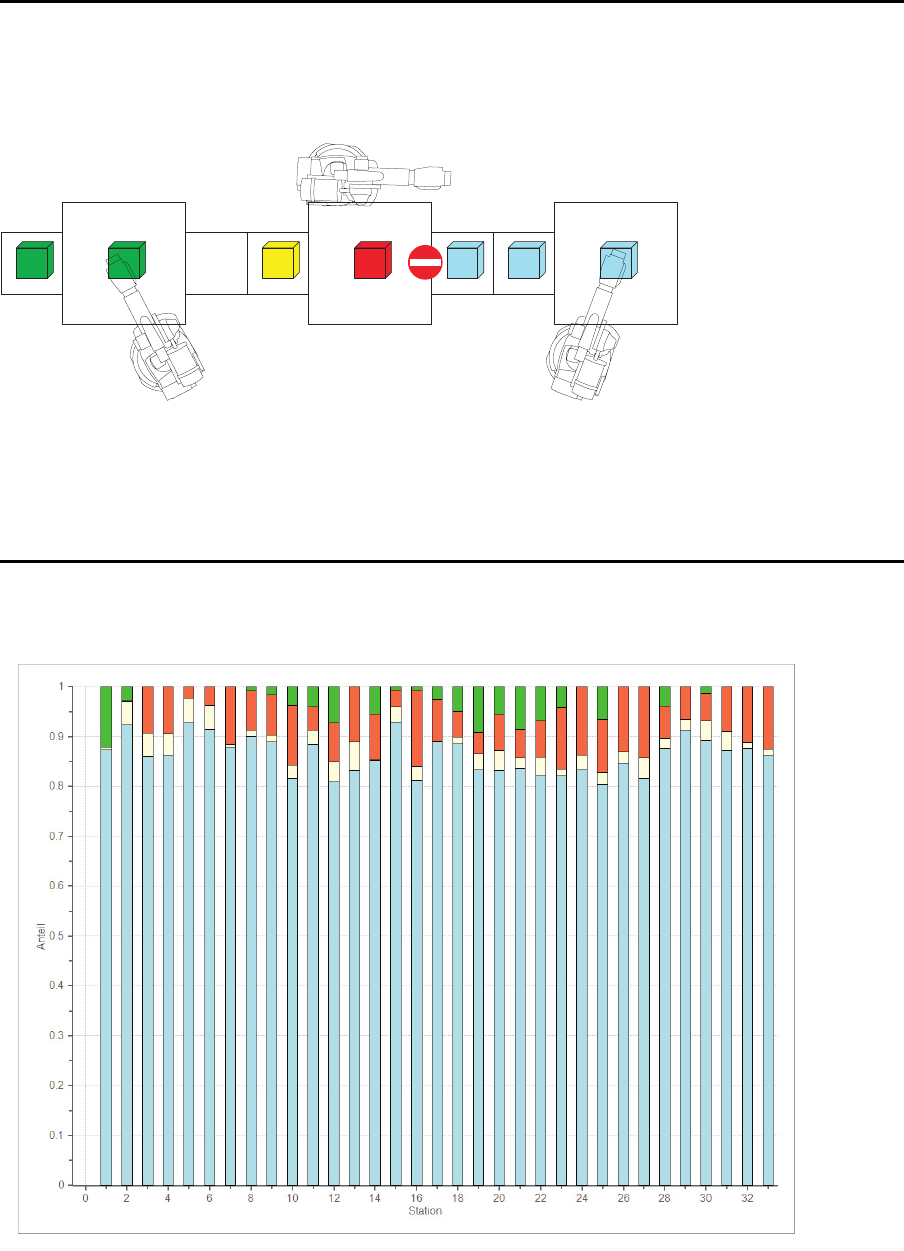
Auslastungsanteile (Praxisfall)
60
Rot=Blocking, Gr¨un=Starving, Gelb=Ausgefallen, Blau=Arbeitend
Literaturhinweis
Tempelmeier (2018), Aufgabe A3.11
Die negativen Auswirkungen des Blocking und Starving k¨onnen durch Einf¨ugen von
Pufferpl¨atzen zwischen den Stationen teilweise kompensiert werden.
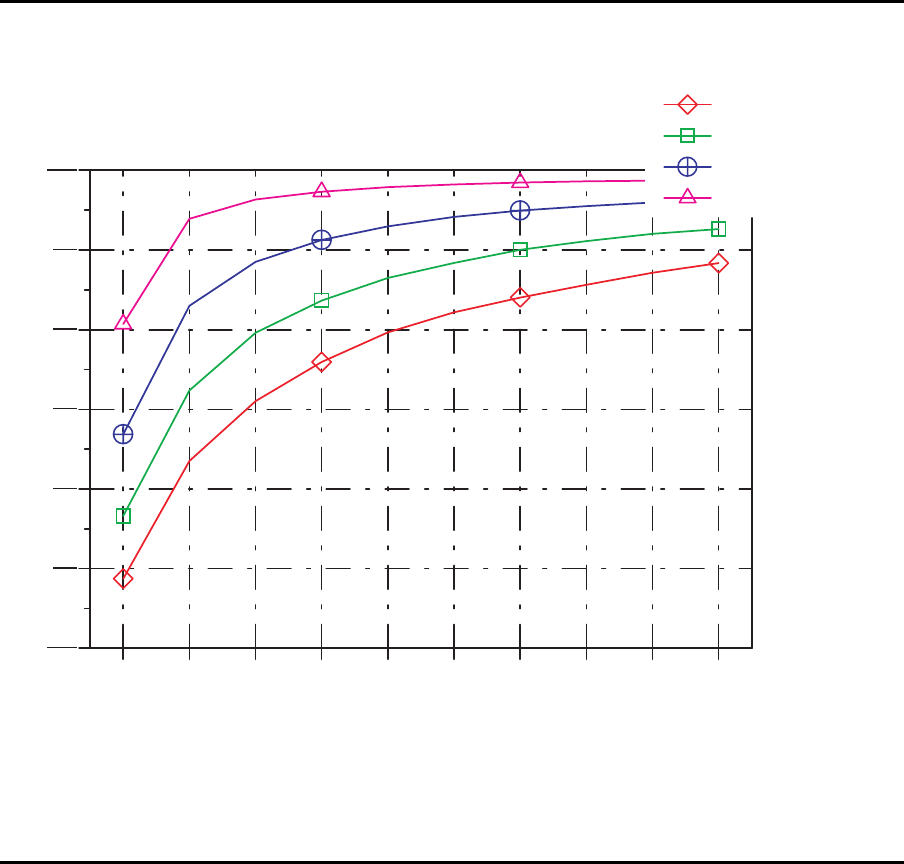
Puffergr¨oßen versus Pr oduktionsrate
0.4
0.5
0.6
0.7
0.8
0.9
1.0
Produktionsrate
0 1 2 3 4 5 6 7 8 9
Puffergröße
CV=0.8
CV=0.6
CV=0.4
CV=0.2
Um allgemeine Aussagen treffen zu k¨onnen, greifen wir auf Ergebnisse zur¨uck, die sich
auf ein System mit 5 identischen Stationen beziehen. Die folgenden Tabellen zeigen
die Auswirkungen der Puffer auf die Produktionsrate bei unterschiedlichen Variationsko-
effizienten.
Puffergr¨oßen versus Pr oduktionsrate
Allgemeine Aussagen: CV = 0.1
61

Puffer
Puffer
CV
X
X −X
min
X
max
−X
min
0 0 0.09095 0
1 10 0.09849 86.86% =
0.9849 − 0.9095
0.9963 − 0.9095
2 20 0.09920 95.04%
3 30 0.09939 97.23%
4 40 0.09958 99.42%
5 50 0.09963 100% =
0.9963 − 0.9095
0.9963 − 0.9095
Puffergr¨oßen versus Pr oduktionsrate
Allgemeine Aussagen: CV = 0.3
Puffer
Puffer
CV
X
X − X
min
X
max
− X
min
0 0 0.07651 0
1 3.33 0.09054 64.12%
2 6.67 0.09405 80.16%
3 10 0.09579 88.11%
4 13.33 0.09657 91.68%
5 16.67 0.09719 94.51%
9 30 0.09839 100%
Puffergr¨oßen versus Pr oduktionsrate
Allgemeine Aussagen: CV = 1.0
Puffer
Puffer
CV
X
X − X
min
X
max
− X
min
0 0 0.04887 0
1 1 0.06078 25.22%
2 2 0.06816 40.85%
4 4 0.07643 58.37%
6 6 0.0819 69.96%
10 10 0.08709 80.95%
20 20 0.09 26 92.62%
30 30 0.09486 97.41%
40 40 0.09567 99.13%
50 50 0.09608 100%
Die Erg ebnisse aus den Tabellen sind im folgenden Bild zusammeng efa ßt. Bei Erh¨ohung
der Puffer um das Zehnfache des Variationskoeffizienten der Bearbeitungszeit werden
80%-85% des maximalen Produktionsmengenverlusts wieder wettgemacht. Weitere Erh¨ohungen
der Puffer bringen nicht mehr viel.
62
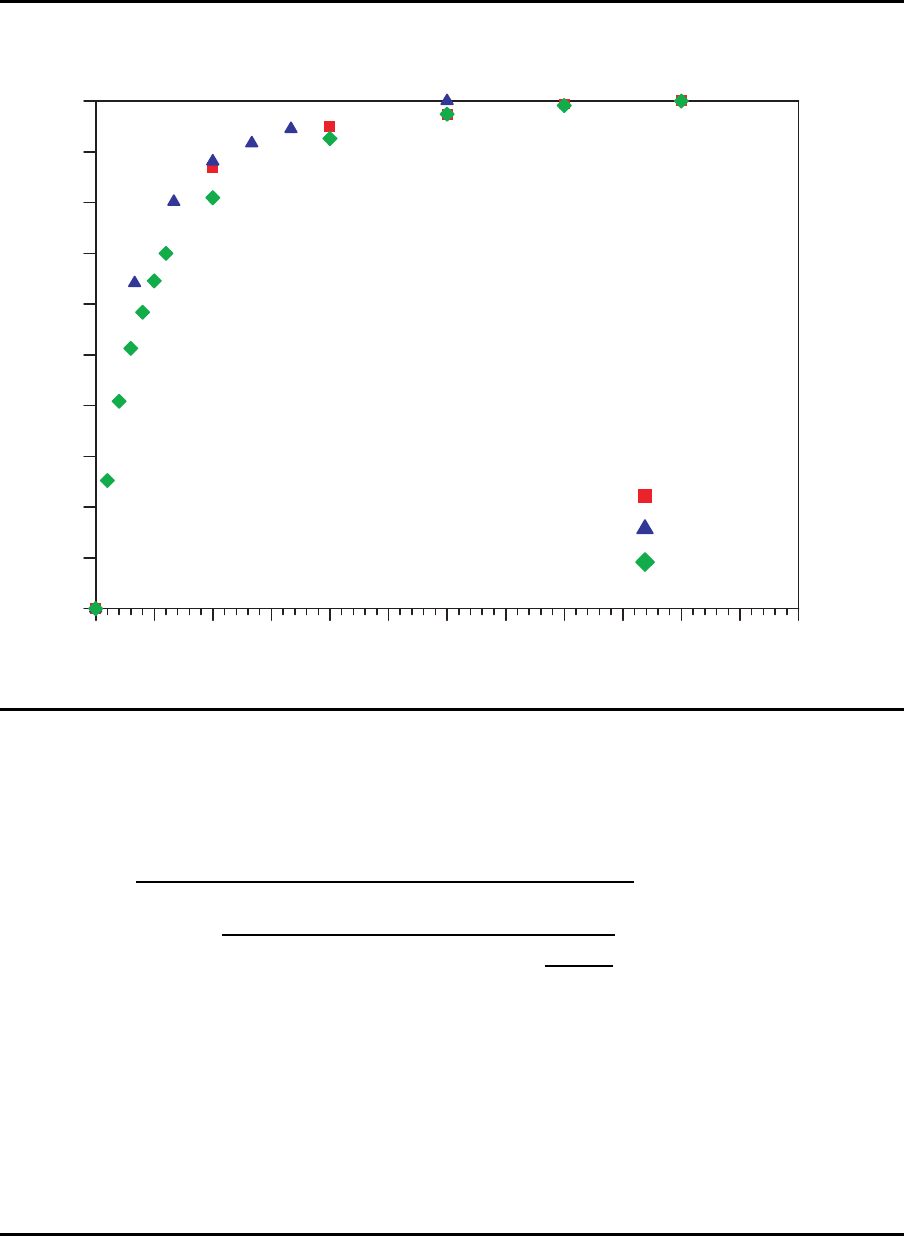
Allerdings: Die Aussagen gelten nur f¨ur den unrealistischen Fall, daß alle Stationen
identisch sind.
Puffergr¨oßen versus Pr oduktionsrate/Variationskoeffizient
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
relative Produktionssteigerung
0 5 10 15 20 25 30 35 40 45 50 55 60
Puffergröße/Variationskoeffizient
CV=0.1
CV=0.3
CV=1.0
Geschlossene Formeln f¨ur balancierte System
Blumenfeld
X(Puffer) =
1
b ·
1 +
1.67 · (M − 1) ·CV
1 + M + 0.31 · CV + 1.67 · M ·
Puffer
2 · CV
Dabie bezeichnet b die mittlere Bearbeitungszeit, M die Anzahl Stationen, CV den Vari-
ationskoeffizienten der Bearbeitungszeiten und Puffer die Anzahl Puffer. Weitere Ap-
proximationsformeln stammen vo n K nott, Martin, Basu und Anderson/Moodie. Diese
Formeln sind ab er nur beschr¨ankt anwendbar, insbes. deshalb, weil sie nicht auf Systeme
mit unterschiedlichen Stationen angewandt werden k¨onnen.
Zur Illustration siehe auch http://www.pom-consult.de/PMTDemo/target4.html
63
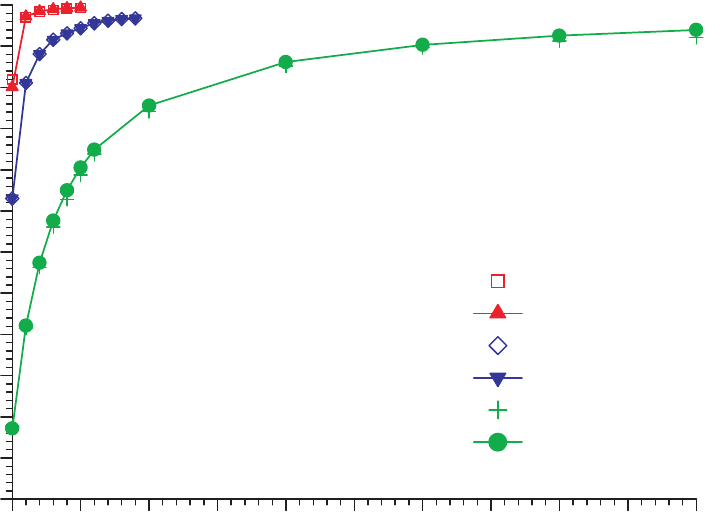
Geschlossene Formeln f¨ur balancierte System
Blumenfeld
0.04
0.04
0.05
0.06
0.06
0.07
0.07
0.08
0.08
0.09
0.09
0.10
0.10
Produktionsrate
0 5 10 15 20 25 30 35 40 45 50
Puffergröße
CV=0.1 (simul)
CV=0.1 (approx)
CV=0.3 (simul)
CV=0.3 (approx)
CV=1.0 (simul)
CV=1.0 (approx)
64
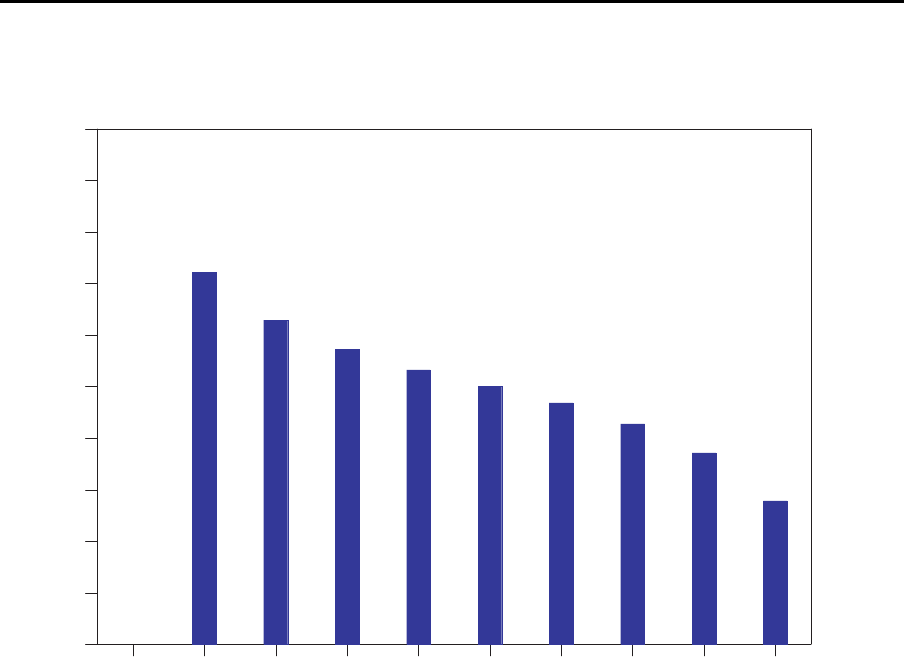
Verteilung der Lagerbest¨ande
M = 10; CV = 0.4; Puffergr¨oßen=1
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
Mittlerer Lagerbestand
1 2 3 4 5 6 7 8 9 10
Puffer vor Station
65
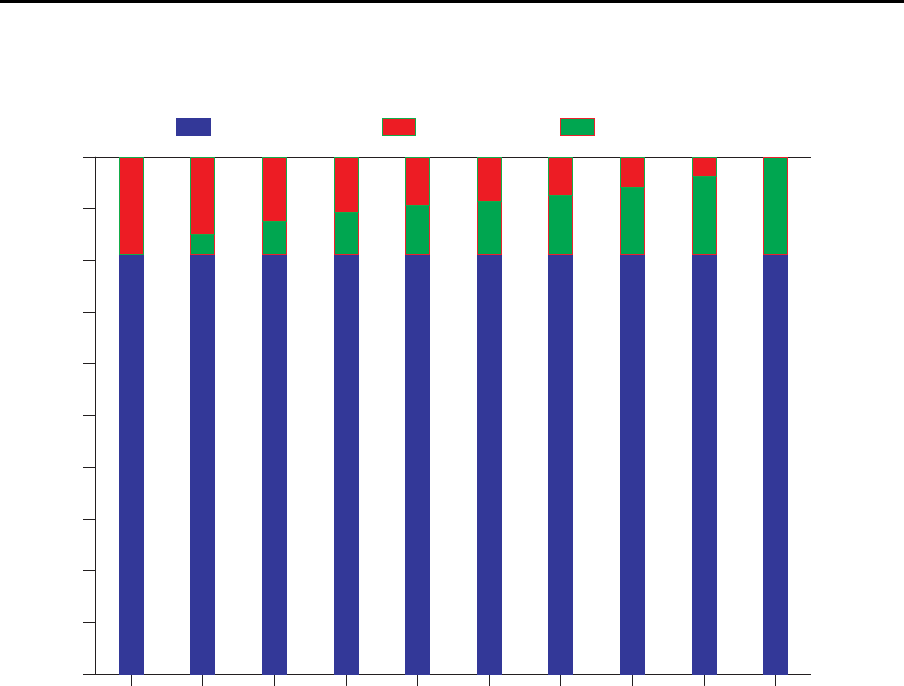
Auslastungsanteile
M = 10; CV = 0.4; Puffergr¨oßen=1
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
Anteil
1 2 3 4 5 6 7 8 9 10
Station
beschäftigt blockiertblockiert leerleer
66
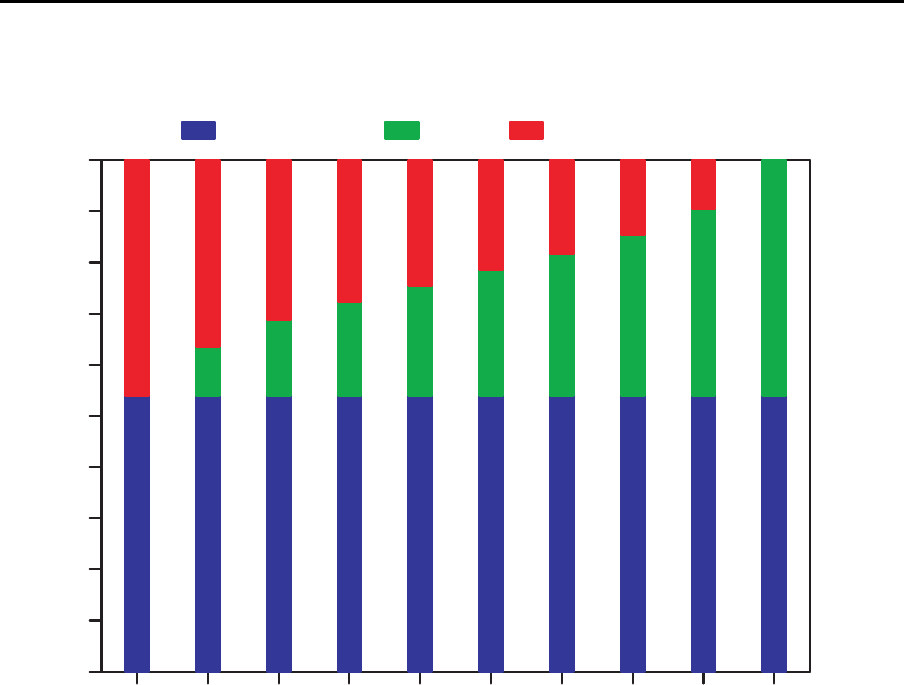
Auslastungsanteile
M = 10; CV = 1.0; Puffergr¨oßen=1
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
A
n
t
e
i
l
1 2 3 4 5 6 7 8 9 10
Station
beschäftigt leer blockiert
67

11.4.1 Praxisbeispiel: Automatisierte Montagelinie
Es wird nun eine automatisierte Montagelinie mit deterministischen und von Station
zu Station unterschiedlichen Bea r beitungszeiten betrachtet. An den Montagestationen
treten nutzungsabh¨angige St¨orungen auf. Die St¨orcharakteristika werden beschrieben
durch Verf¨ugbarkeiten und mittlere Repara turzeiten (MTTR). An zwei Stationen (20
und 21) sind die St¨orungen besonders ausgepr¨agt. Die Systemdaten sind in der folgenden
Tabelle zusammengefaßt:
Station Puffer Bearbeitungszeit Verf¨ugbarkeit MTTR
1 – 5.100 0.983 29.69
2 9 5.100 0.990 35.89
3 12 5.300 0.975 34.52
4 12 5.300 0.935 44.40
5 9 3.800 0.992 27.27
6 6 5.200 0.961 30.40
7 5 5.200 0.943 54.97
8 6 5.000 0.968 33.98
9 10 3.500 1.000 –
10 9 5.100 0.941 27.75
11 30 5.500 0.964 47.53
12 6 5.300 0.977 45.23
13 9 4.700 0.990 61.28
14 9 3.500 1.000 –
15 6 5.000 0.984 35.43
16 7 5.100 0.989 33.19
17 8 4.100 0.992 214.69
18 6 4.900 0.979 51.07
19 6 4.900 0.979 51.64
20 7 4.900 0.894 75.83
21 31 6.100 0.830 45.39
22 128 5.100 0.958 229.85
23 128 5.100 0.958 229.85
459
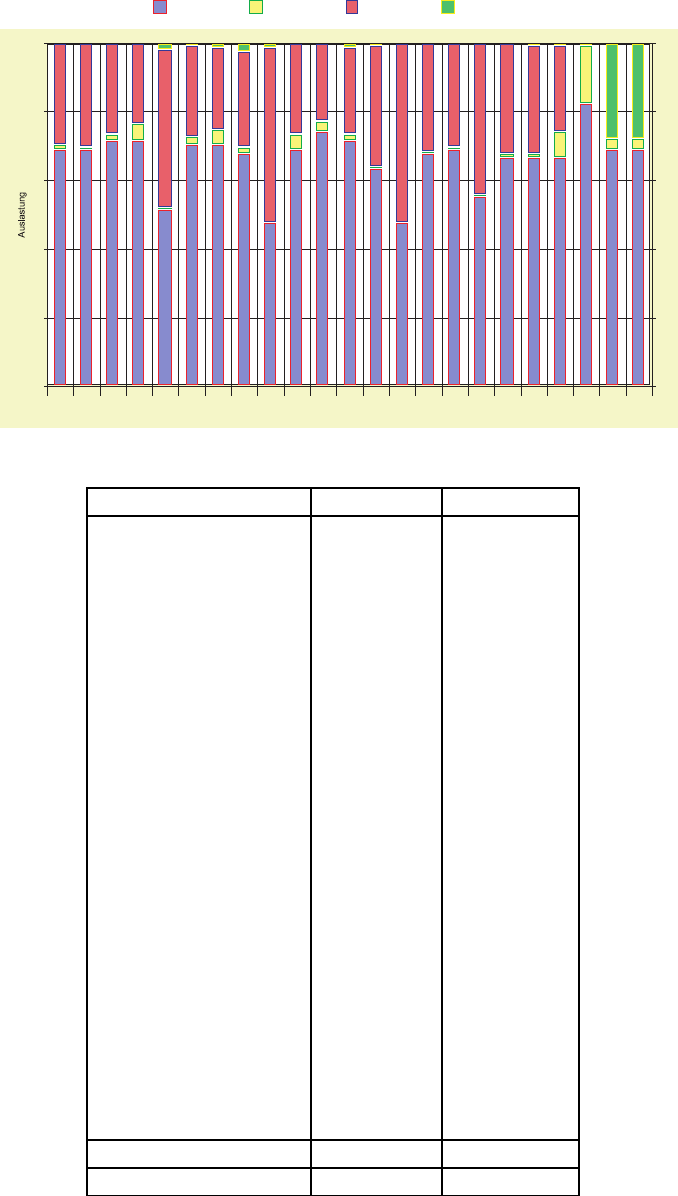
F¨uhrt man eine Leistungsanalyse dieses FPS durch, dann erh¨alt man f¨ur die gegebene
Pufferkonfiguration die im folgenden Bild dargestellten Auslastungsanteile. Man erkennt
deutlich, daß die Station 20 wegen ihrer geringen Verf¨ugbarkeit den Materialfluß erheblich
blockiert. D ies dr¨uckt sich in den hohen Blockieranteilen aller Vorg¨angerstationen aus.
Man kann auch vermuten, daß die hohe Pufferzahl vor der Station 23 nicht ben¨otigt wird.
68
0.0
0.2
0.4
0.6
0.8
1.0
0.0
0.2
0.4
0.6
0.8
1.0
1 2 3 4 5 6 7 8 9 1 0 1 1 12 13 1 4 1 5 16 1 7 1 8 1 9 2 0 2 1 22 2 3
Station
beschäftigt gestört blockiert leer
Station Puffer(Alt) Puffer(Opt)
1 – –
2 9 0
3 12 0
4 12 0
5 9 0
6 6 0
7 5 0
8 6 0
9 10 0
10 9 0
11 30 1
12 6 0
13 9 6
14 9 3
15 6 1
16 7 8
17 8 6
18 6 2
19 6 10
20 7 11
21 31 52
22 128 62
23 128 30
Gesamtanzahl Puffer 459 192
Produktionsrate 0.13474 0.13474
69
0.0
0.2
0.4
0.6
0.8
1.0
0.0
0.2
0.4
0.6
0.8
1.0
1 2 3 4 5 6 7 8 9 1 0 1 1 12 13 1 4 1 5 16 1 7 1 8 1 9 2 0 2 1 22 2 3
Station
beschäftigt gestört blockiert leer
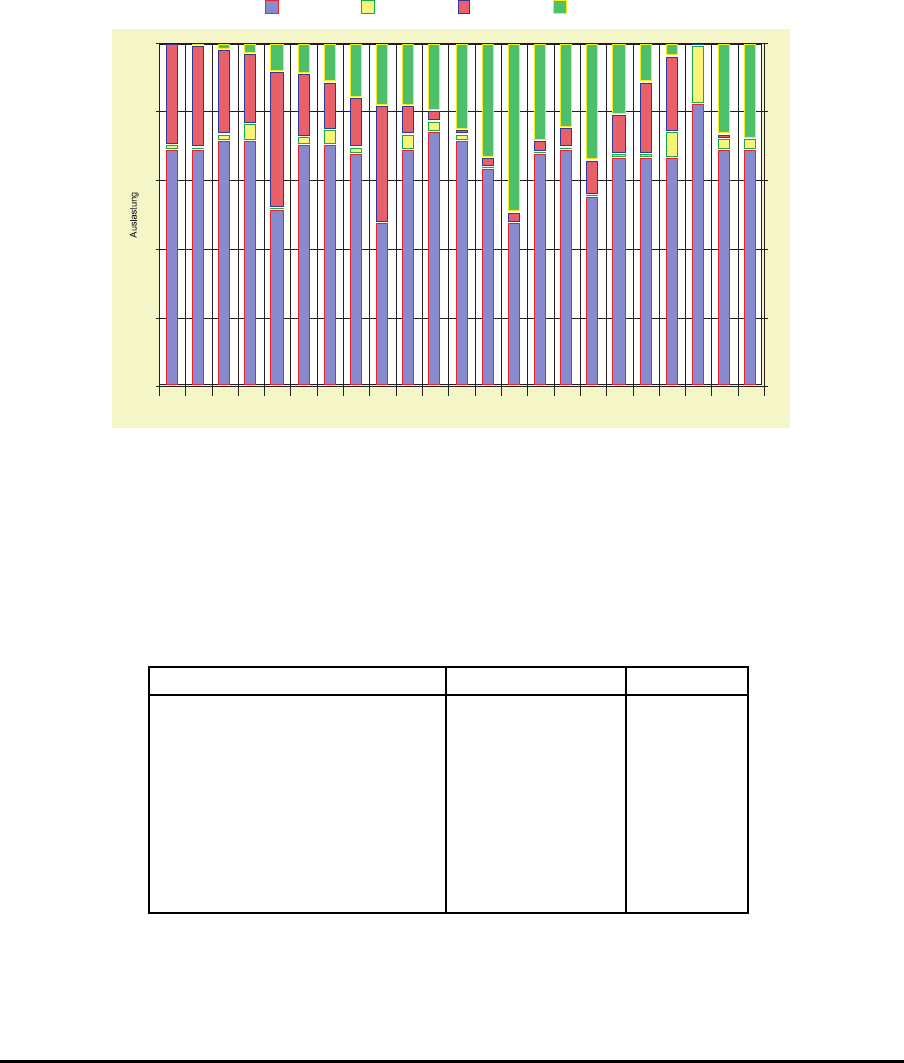
Man kann auch untersuchen, ob organisatorische oder technische Maßnahmen
zur Beeinflussung der St¨orcharakteristika einzelner Stationen zu einem Leistungsanstieg
f¨uhren. Erh¨oht man z. B. durch technische Maßnahmen die Verf¨ugbarkeit der Station
21 von 83% auf 90% (bei konstanter MTTR, d. h. durch Verl¨angerung der st¨orungsfreien
Laufzeiten), dann steigt die Produktionsrate des FPS (bei Annahme der optimierten
Pufferkonfiguration) wie folgt:
Verf¨ugbarkeit der Station 21 Produktionsrate %-Anstieg
83% 0.13474 -
84% 0.13631 1.16%
85% 0.13777 2.26%
86% 0.13913 3.26%
87% 0.14024 4.08%
88% 0.14100 4.64%
89% 0.14146 4.99%
90% 0.14173 5.19%
Alternativ k¨onnte man auch durch organisatorische Maßnahmen die St¨ordauer (MTTR)
reduzieren, z. B. dadurch, daß man das Entst¨orsystem r eor ganisiert und es dadurch zu
k¨urzeren Wartezeiten der Stationen auf den Beginn des Entst¨orvor ganges kommt.
Weitere Informationen
Internet
Weitere Informationen, Praxisb eispiele etc. sind im Internet zu finden:
http://www.produktion-und-logistik.de → Fabrikplanung
70

Teil VII
Fließproduktionssy steme mit
begrenzten Puffern
12 Systeme ohne Puffe r , Pufferg r ¨oße=0
Typen von Subsystemen
Systemverf¨ugbarkeit = Produkt der Stationsverf¨ugbar keiten
V
s
=
m
Y
m=1
V
m
Pizza-Fabrik
Machine λ MTTF r MTTR Verf¨ugbarkeit
1 0.0089 112.36 4.6512 0.21 0.9981
2 0.0410 24.39 0.7491 1.33 0.9481
3 0.0001 10000.00 0.9901 1.01 0.9999
4 0.0980 10.20 2.9762 0.34 0.9681
5 0.0074 135.32 0.7994 1.25 0.9908
6 0.0095 105.71 1.1751 0.85 0.9920
7 0.0030 334.45 0.3044 3.29 0.9903
8 0.0201 49.85 0.6988 1.43 0.9721
9 0.0096 104.49 1.9531 0.51 0.9951
10 0.0069 144.09 2.1882 0.46 0.9968
11 0.0020 510.20 0.6523 1.53 0.9970
12 0.0169 59.17 1.6 0.63 0.9895
λ =Ausfallrate (Kehrwert von MTTF) r =Reparaturrate (Kehrwert von MTTR)
Solche Konfigura t ionen sind i. d. R. technisch determiniert.
13 Zwei-Stationen-Systeme
Da große Fließproduktionssysteme mit vielen Stationen und/oder großen Puffern auch
bei vereinfachenden Annahmen nicht exakt analysiert werden k¨onnen, betrachten wir
zun¨achst den Spezialfall, daß ein Fließproduktionssyst em aus zwei Stationen besteht.
F¨ur derartige Systeme kann man unter bestimmten Annahmen alle Leistungskenngr¨oßen
exakt berechnen.
71
13.1 Merkmale
Typen von Subsystemen
• Weitergabe der Werkst ¨ucke
• Bearbeitungszeiten
• St¨orungen
Typen von Subsystemen
• exp onent ial-verteilte Bearbeitungszeiten, keine St¨orungen,
• allgemein-verteilte Bearbeitungszeiten, keine St¨orungen,
• deterministische Bearbeitungszeiten, an allen Stationen identisch, St¨orungen
• deterministische Bearbeitungszeiten, stationsspezifisch, St¨orungen
Wir betrachten jetzt den Fall eines Zwei-Stationen-Systems, in dem die Bearbeitungszeiten
exponentialverteilt sind. Ein solches System kann man auf zweierlei Weise analysieren
1. mit einem Markov-Modell
2. mit einem M/M/1/N-Warteschlangenmodell (mit begrenzter Anzahl Kunden
im System)
13.2 Markov-Modell eines Zwei-Stationen-Systems
Markov-Modell
Expone ntialverteilte Bearbeitungszeiten
Station m Station m+1
0 Puffer
Bearbeitungsrate
Station m
=
Ankunftsrate
Bearbeitungsrate
Station m+1
=
Bedienrate
72
Markov-Modell
Zust¨ande
(n
1
, n
2
)
n
m
– Anzahl der Werkst¨ucke, die auf Station m warten oder dort in Bearbeitung sind.
Bei Station 2 also einschl. des blockierten Werkst¨ucks, das darauf wartet, die Station 1
zu verla ssen und in den Puffer vor Station 2 zu gelangen.
Dies ist a uch die Notation im Produktions-Management-Trainer.
Mit dem Markov-Modell werden die station¨aren Wahrscheinlichkeiten f¨ur die Zust¨ande,
die das System annehmen kann, als Funktion der Bearbeitungsraten an den Stationen
bestimmt. Aus diesen Zustandswa hrscheinlichkeiten kann man dann die Produktionsrate
des Systems und den Lagerbestand ableiten.
Markov-Modell
Zust¨ande – Beispiele, Puffergr¨oße c = 0
n Station 1 Puffer Station 2 Zustand
– leer leer leer geht nicht
0 arbeitet leer leer (1,0)
1 arbeitet leer arbeitet (1,1)
2 blockiert 1 Werkst ¨uck arbeitet (0,2)
Markov-Modell
Zust¨ande – Beispiele, Puffergr¨oße c = 1
n Station 1 Puffer Station 2 Zustand
– leer leer leer geht nicht
0 arbeitet leer leer (1,0)
1 arbeitet leer arbeitet (1,1)
2 arbeitet 1 Werkst¨uck ar beitet (1,2)
3 blockiert 1 Werkst ¨uck arbeitet (0,3)
Markov-Modell
Zust¨ande – Beispiele, Puffergr¨oße c = 2
n Station 1 Puffer Station 2 Zustand
0 arbeitet leer leer (1,0)
1 arbeitet leer arbeitet (1,1)
2 arbeitet 1 Werkst¨uck arbeitet (1,2)
3 arbeitet 2 Werkst¨ucke arbeitet (1,3)
4 blockiert 2 Werkst ¨ucke arbeitet (0,4)
73
Ingesamt c + 3 Zust¨ande
In der folgenden
¨
Ubergangsmatrix geht das System vom Zustand 1 in den Zustand 2
¨uber, wenn an Station 1 das Ereignis ’Bearbeitungsende’ auftritt (mit der Wahrschein-
lichkeit λ · h) und a n Station 2 das Ereignis ’Bearbeitungsende’ nicht auftritt (mit der
Wahrscheinlichkeit 1 − µ · h)
Markov-Modell
¨
Ubergangswahrscheinlichkeiten, Puffergr¨oße c = 0
nach
von 0 (1,0) 1 ( 1,1) 2 ( 0,2)
0 (1 − λ · h): λ · h:
(1,0)
kein Bearbeitungsende an
Station 1
Bearbeitungsende an Sta-
tion 1
1 (1 − λ · h) ·µ · h: (1 −λ · h) ·(1 − µ · h): λ · h ·(1 − µ · h):
(1,1)
kein Bearbeitungsende
an Sta tion 1, Bear-
beitungsende an Station
2
kein Bearbeitungsende an
Station 1, kein Bear-
beitungsende an Station 2
Bearbeitungsende an
Station 1 , kein Bear-
beitungsende an Station
2
2 µ ·h: (1 −µ · h):
(0,2)
Bearbeitungsende an Sta-
tion 2
kein Bearbeitungsende an
Station 2
Siehe auch http:// www.produktion-und-logistik.de/produktionundlogistik-478.html.
¨
Ublicherweise stellt man die Dynamik des Systems in einem
¨
Ubergangsraten-Diagramm
dar, in dem f¨ur jeden Zustand ein Knoten eingef¨uhrt wird und die m¨oglichen Zustands¨uberg¨ange
durch Pfeile dargestellt werden. Die Pfeilbewertungen sind die Raten λ (hier: Bear-
beitungsrate der Station 1) und µ (hier: Bearbeitungsrate der Station 2).
Gesucht:
P
n
= station¨are Zustandswahrscheinlichkeit
F¨ur jeden Knot en (Zustand) im
¨
Ubergangsraten-Diagramm muß dann gelten:
Erwarteter Fluß in den Knoten = Erwarteter Fluß aus dem Knoten
Im folgenden
¨
Ubergangsgraphen ergibt sich z. B. f¨ur Knoten 1:
λ ·P
0
+ µ · P
2
= (λ + µ) · P
1
(1)
74
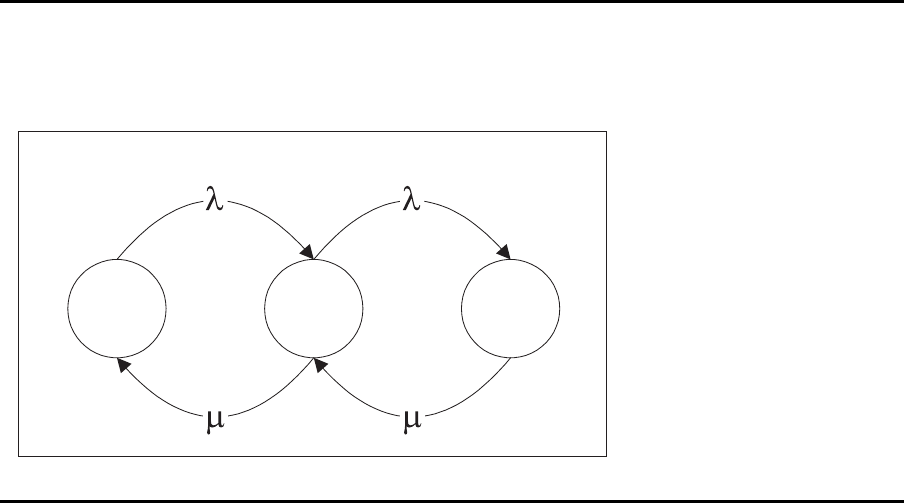
Markov-Modell
¨
Ubergangsraten-Diagramm f¨ur c = 0
0 1 2
Markov-Modell
Berechnung f¨ur c = 0
P
n
= station¨are Zustandswahrscheinlichkeit
− λ · P
0
+ µ · P
1
= 0
λ · P
0
− (λ + µ) · P
1
+ µ · P
2
= 0
λ · P
1
− µ · P
2
= 0
(2)
Damit liegt ein Gleichungssystem mit n Gleichungen und n Unbekannten vor. Da die
Summe der Zustandswahrscheinlichkeiten 1 ergeben muß, ersetzen wir jetzt noch eine
Gleichung, z. B. die letzte, entsprechend:
− λ · P
0
+ µ · P
1
= 0
λ · P
0
− (λ + µ) · P
1
+ µ ·P
2
= 0
P
0
+ P
1
+ P
2
= 1
(3)
Zur L¨osung dieses Gleichungssystems invertiert man die
¨
Ubergangsmatrix und multi-
pliziert die Inverse mit dem Vektor der rechten Seite. F¨ur λ = µ = 0.8 ist das in der
folgenden Excel-Tabelle dargestellt:
75
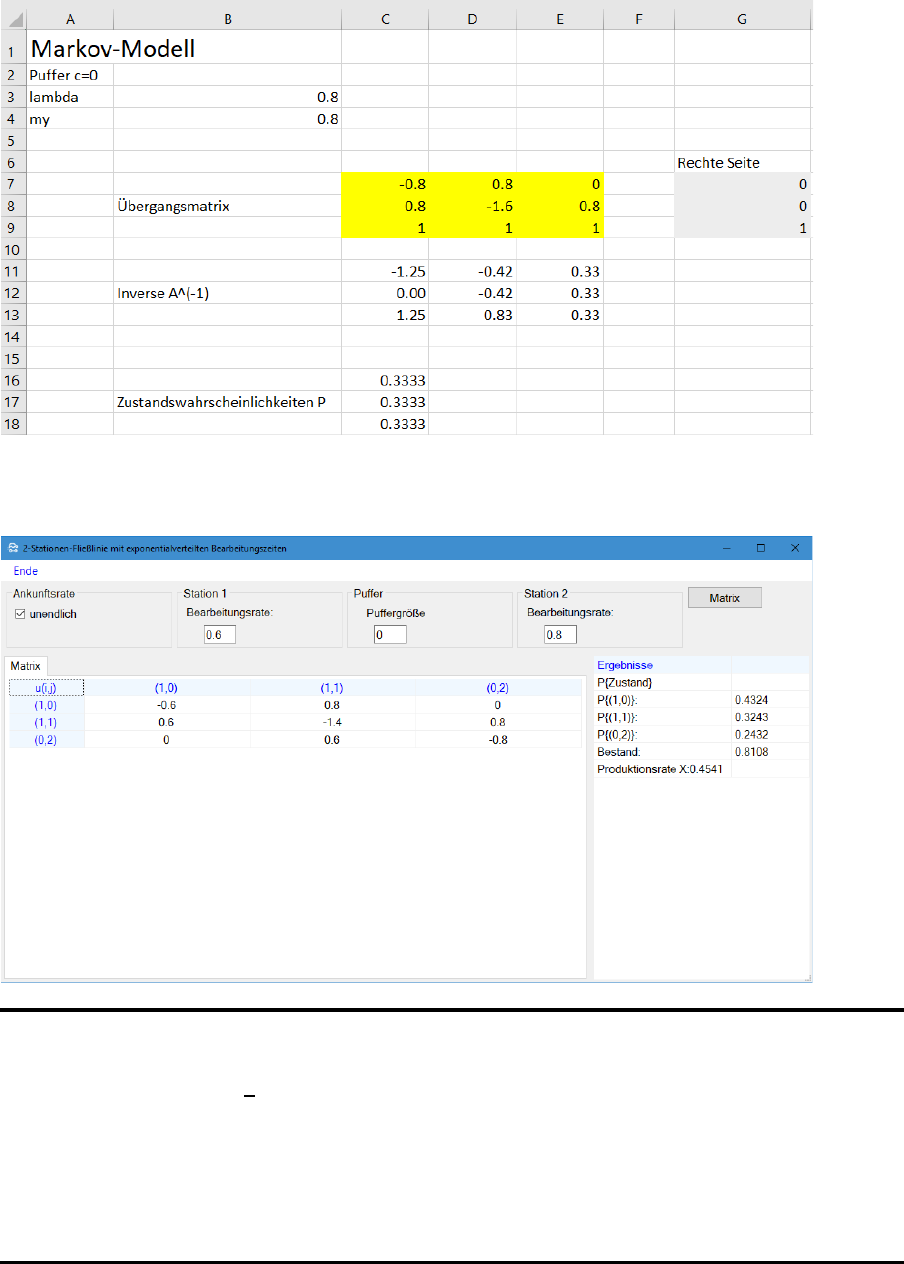
Im Produktions-Management-Trainer sieht das so aus (die letzte Gleichung wird erst vor
der L¨osung des Gleichungssystems intern durch
P
N+1
n=0
P
n
= 1 ersetzt):
Markov-Modell
Berechnung von P
0
f¨ur
λ
µ
6= 1
λ · P
0
= µ · P
1
(a)
(λ + µ) · P
1
= λ · P
0
+ µ · P
2
(b)
µ · P
2
= λ · P
1
(c)
(4)
Markov-Modell
76

Aus (4a) fo lgt
P
1
=
λ
µ
· P
0
(5)
Aus (4b) folgt
P
2
=
λ
µ
· P
1
+ P
1
−
λ
µ
· P
0
=
λ
µ
2
· P
0
+
λ
µ
·P
0
−
λ
µ
· P
0
=
λ
µ
2
· P
0
(6)
Außerdem gilt:
P
0
+ P
1
+ P
2
= 1
(7)
Markov-Modell
Einsetzen:
P
0
+
λ
µ
· P
0
+
λ
µ
2
· P
0
= 1
(8)
Daraus folgt:
P
0
=
1
1 +
λ
µ
+
λ
µ
2
(9)
Markov-Modell
Die Summe der geometrischen Reihe (im Nenner von (9)):
s
n
= a
0
+ a
1
+ ... + a
n
= a · (1 + q
1
+ q
2
+ ... + q
n
)
(10)
betr¨agt
s
n
= a ·
1 − q
n+1
1 − q
(11)
Im vorliegenden Fall ergibt sich (n = 2, a = 1):
P
0
=
1
1 −
λ
µ
3
1 −
λ
µ
(12)
77

Markov-Modell
oder
P
0
=
1 −
λ
µ
1 −
λ
µ
3
(13)
Diese Formel gilt f¨ur c = 0 mit c + 3 = 3 m¨oglichen Zust¨anden.
Allgemein gilt:
λ · P
0
= µ · P
1
(a)
(λ + µ) · P
n
= λ · P
n−1
+ µ · P
n+1
1 ≤ n ≤ N (b)
µ · P
N
= λ · P
N−1
(c)
(14)
P
0
=
1 − (
λ
µ
)
1 − (
λ
µ
)
N+1
=
1 − ρ
1 − ρ
N+1
(15)
Der Index der Zust¨ande l¨auft von 0 bis N, also haben wir insgesamt N + 1 = c + 3
Zust¨ande.
Markov-Modell
F¨ur λ = µ = x bzw. ρ = 1 wird aus (4):
x · P
0
= x · P
1
(a)
(x + x) · P
1
= x · P
0
+ x · P
2
(b)
x · P
2
= x · P
1
(c)
(16)
Aus (a) folg t P
0
= P
1
Aus (c) folgt P
2
= P
1
Also P
0
= P
1
= P
2
= Y
Wegen P
0
+ P
1
+ P
2
= 1 ergibt sich Y + Y + Y = 1 bzw. 3 · Y = 1
oder Y =
1
3
und damit P
0
= P
1
= P
2
=
1
3
78
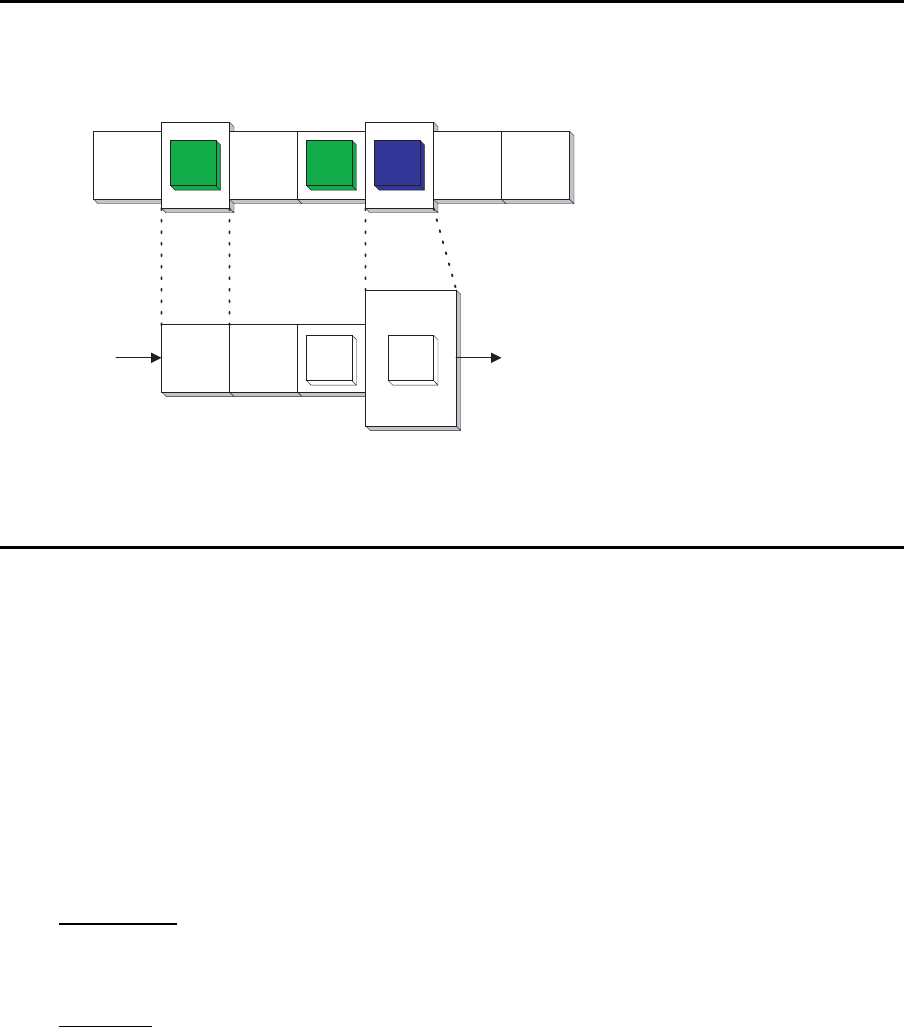
13.3 Wartesch langenmodell eines Zwei-Stationen-Systems
Man kann das Zwei-Stationen-System auch als ein Warteschlangensystem mit begrenzter
Anzahl von Kunden, N
max
, modellieren. Da s sieht dann so aus:
(M/M/1) : (GD/N
max
/∞)-Warteschlangenmodell
Station m Station m+1
Warteschlangensystem mit
maximal 4 Kunden
2 Puffer
Bearbeitungsrate
Station m
=
Ankunftsrate
Bearbeitungsrate
Station m+1
=
Bedienrate
1234
(M/M/1) : (GD/N
max
/∞)-Warteschlangenmodell
Bezeichnen wir die Puffergr¨oße zwischen beiden Statio nen mit c
m,m+1
, dann gilt
N
max
= c
m,m+1
+ 2
Die Gr¨oße N
max
ist hier die maximale Anzahl der Kunden im Wartesystem.
F¨ur dieses Warteschlangenmodell betr¨agt die Wahrscheinlichkeit, daß sich keine Kunden
im System befinden:
P
0
=
1 − ρ
1 − ρ
N
max
+1
ρ 6= 1
P
0
=
1
N
max
+ 1
ρ = 1
Produktionsrate des Zwei-Stationen-Systems:
X(m, m + 1) = µ
d
(m, m + 1) · (1 − P
0
)
Diese Produktionsrate verwenden wir im weiter unten dargestellten Dekompositionsansatz.
79
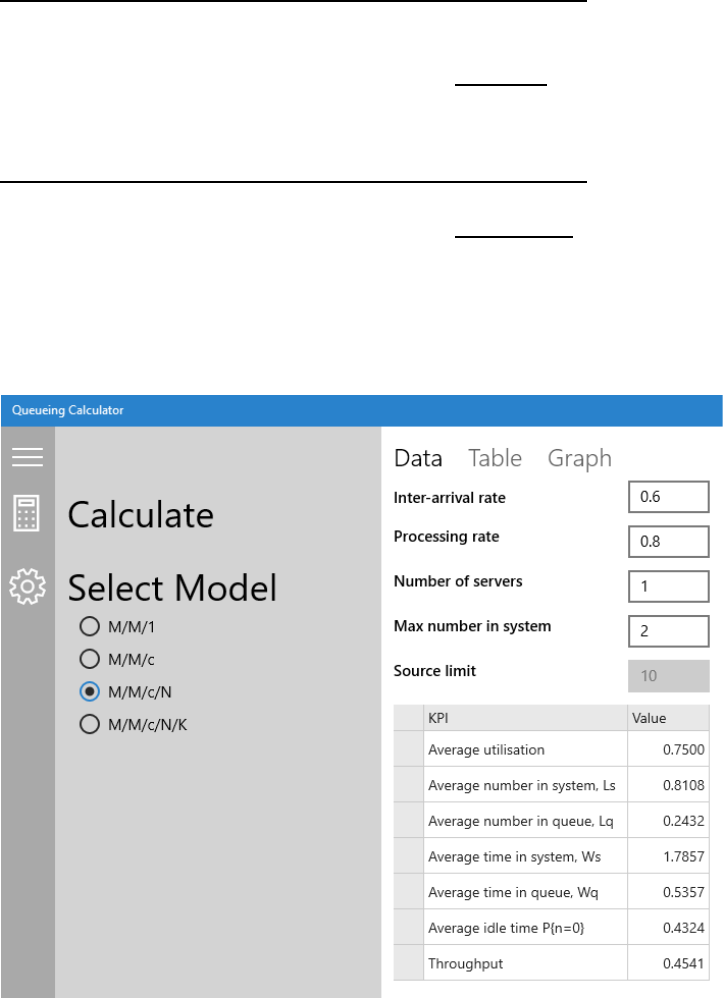
Vergleich der beiden Modellierungskonzepte:
Markov-Modell:
Zust¨ande 0, 1, . . . , N
Anzahl Zust¨ande Puffergr¨oße + 3
P
0
P
0
=
1 − ρ
1 − ρ
N+1
(M/M/1) : (GD/N
max
/∞)-Modell:
Maximale Anzahl Kunden Puffergr¨oße + 2
P
0
P
0
=
1 − ρ
1 − ρ
N
max
+1
Also: N
max
= N + 1
F¨ur das obige Beispiel mit λ = 0.6 und µ = 0.8 erh¨alt man mit der Windows Store-App
’Queueing Calculator’ folgende Ergebnisse:
80