
5
Teil VI
Fließproduktionssysteme,
Stochastisch
10 Stochasti sche Bedingungen
In der Praxis muß oft davon ausgegangen werden, daß die tats¨achlichen Bearbeitungszei-
ten bzw. die Zeitspannen, w¨ahrend deren sich die Werkst¨ucke an den Stationen aufhal-
ten, mehr oder weniger großen zuf¨alligen Schwankungen unterliegen. Diese Schwankun-
gen zwingen i. a. dazu, die einzelnen Stationen zu entkoppeln, z. B. durch Einf¨ugen von
Puffern.
10.1 Zufallsein߬usse
Zufallsein߬usse
Zuf¨allige Schwan k ung en d er Aufenthaltsdauer eines Werkst¨ucks an einer Station
• Schwankungen der Bearbeitungszeiten
• Mehrere Produktarten bzw. -varianten mit unterschiedlichen Bearbeitungszeiten
• St¨orungen
• Produktionsfehler
• Begrenzte Anzahl Werkst¨ucktr¨ager
Zuf¨allige Schwankungen der Bearbeitungszeiten
44
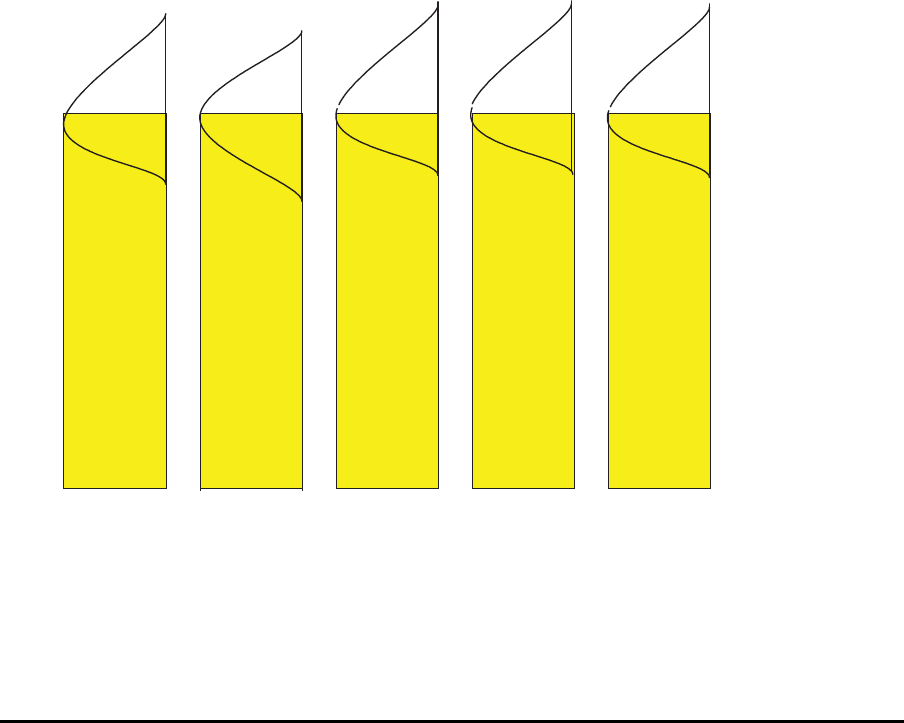
Arbeitslast
Stationen
Station 1:
33 Sekunden
Station 2:
33 Sekunden
Station 3:
33 Sekunden
Station 4:
33 Sekunden
Station 5:
33 Sekunden
Obwohl die Mittelwerte der Stationszeiten identisch sind, k¨onnen die Bearbeitungszeiten
der einzelnen Werkst¨ucke an einer Station zuf¨allig schwanken.
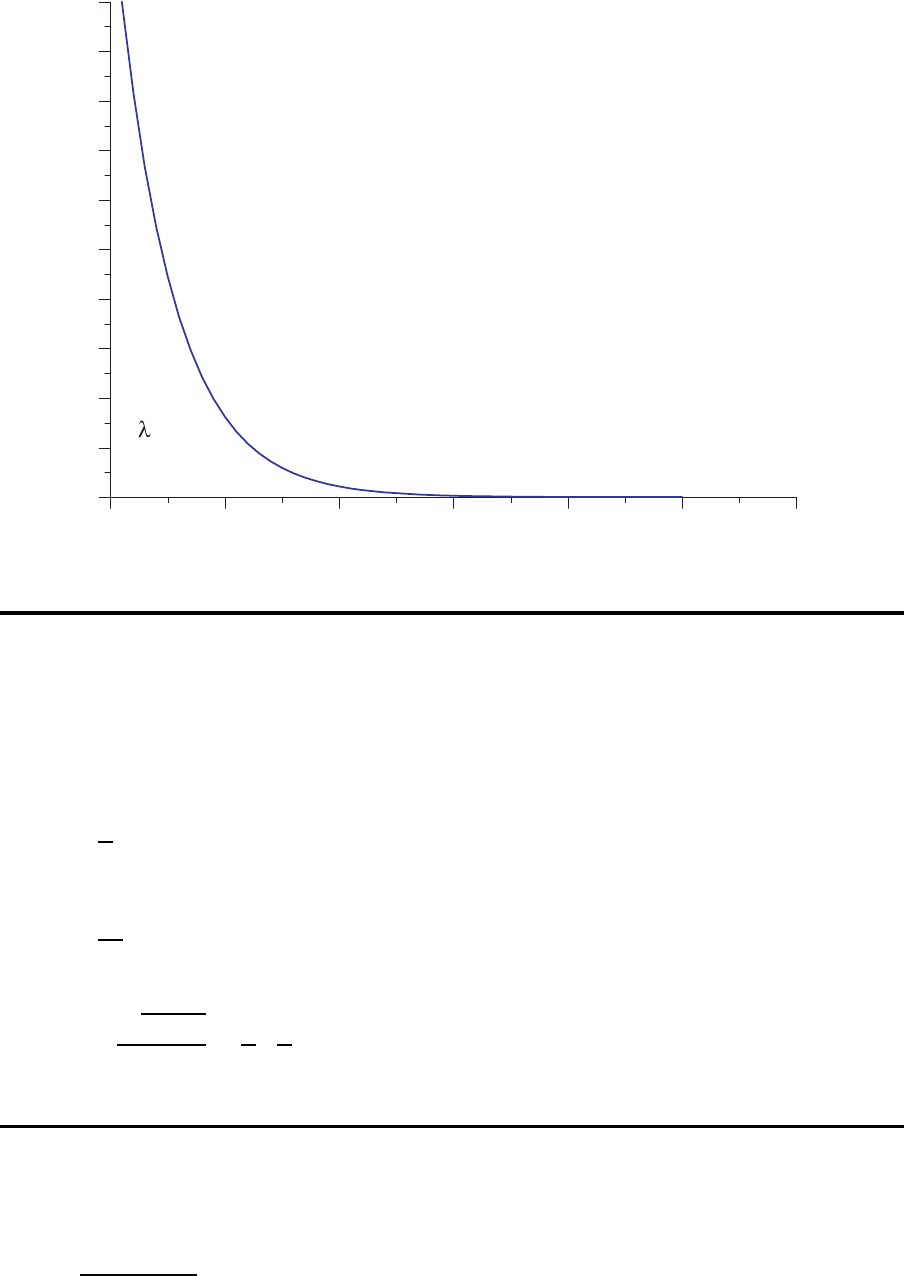
In analytischen Modellen wird auf theoretische Verteilungen zur¨uckgegriffen. Wegen ihrer
mathematischen Eigenschaften wird oft die Exponentialverteilung unterstellt.
Exponentialverteilt e Bearbeitungszeiten
f(x) = λ · e
−λ·x
x ≥ 0
45
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
Dichtefunktion f(x)
0 10 20 30 40 50 60
x
=1
Exponentialverteilt e Bearbeitungszeiten
f(x) = λ · e
−λ·x
x ≥ 0
E{X} =
1
λ
V {X} =
1
λ
2
CV {X} =
p
V {X}
E{X}
=
1
λ
·
λ
1
= 1
Gamma-verteilte Bearbeitungszeiten
f(x) =
α
k
x
k−1
e
−αx
Γ (k)
, x ≥ 0
46
0.00
0.02
0.04
0.06
0.08
0.10
0.12
0.14
0.16
0.18
0.20
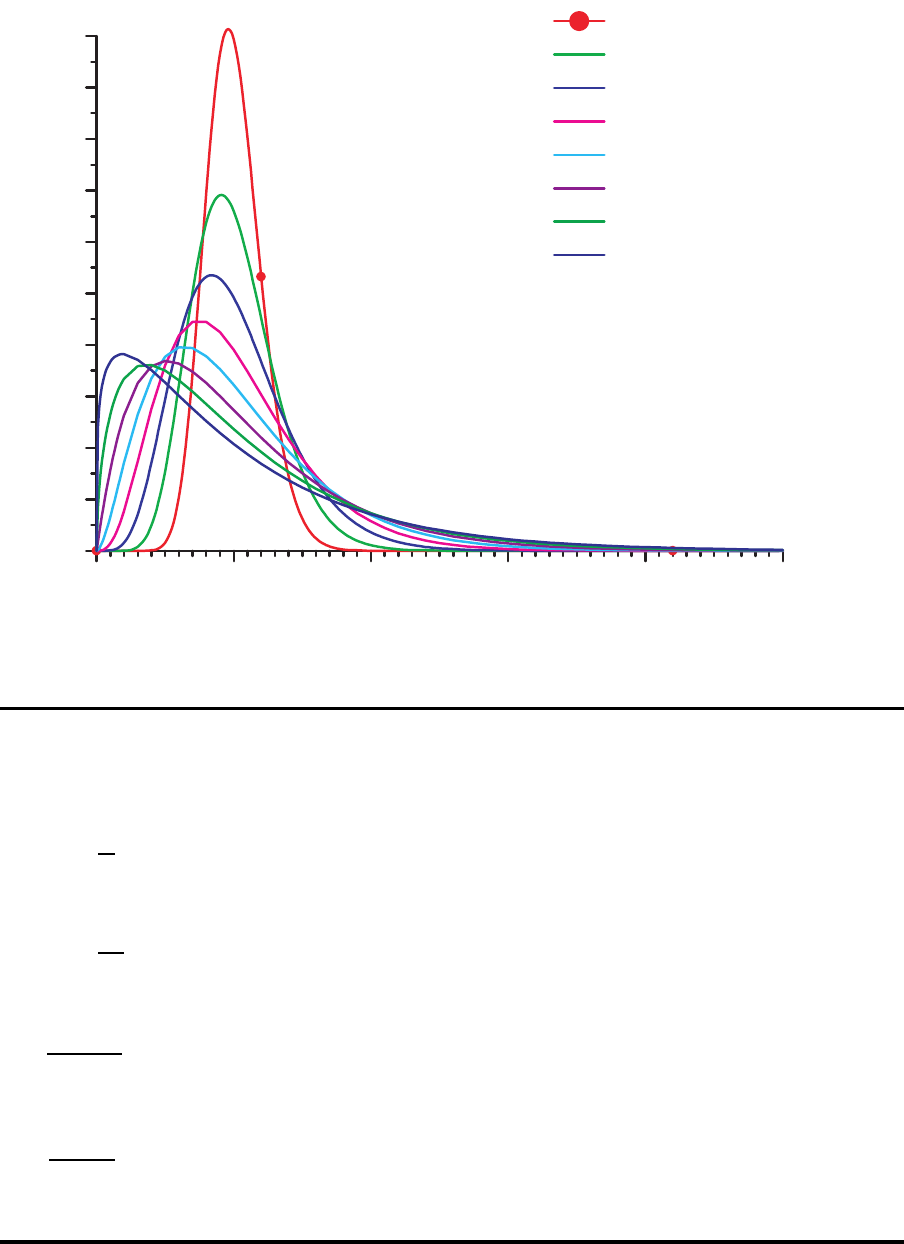
Dichtefunktion f(x)
0 10 20 30 40 50
Bearbeitungszeit
E{X}=10;V{X}=4
E{X}=10; V{X}=9
E{X}=10;V{X}=16
E{X}=10;V{X}=25
E{X}=10;V{X}=36
E{X}=10;V{X}=49
E{X}=10;V{X}=64
E{X}=10;V{X}=81
Zur Modellierung realer Bearbeitungszeiten in der Praxis eignet sich die Gamma-Verteilung,
mit der auch Variationskoeffizienten <> 1 abgebildet werden k¨onnen.
Gamma-verteilte Bearbeitungszeiten
E{X} =
k
α
Erwartungswert
V {X} =
k
α
2
Varianz
k =
E{X}
2
V {X}
Formparameter
α =
E{X}
V {X}
Lageparameter
47
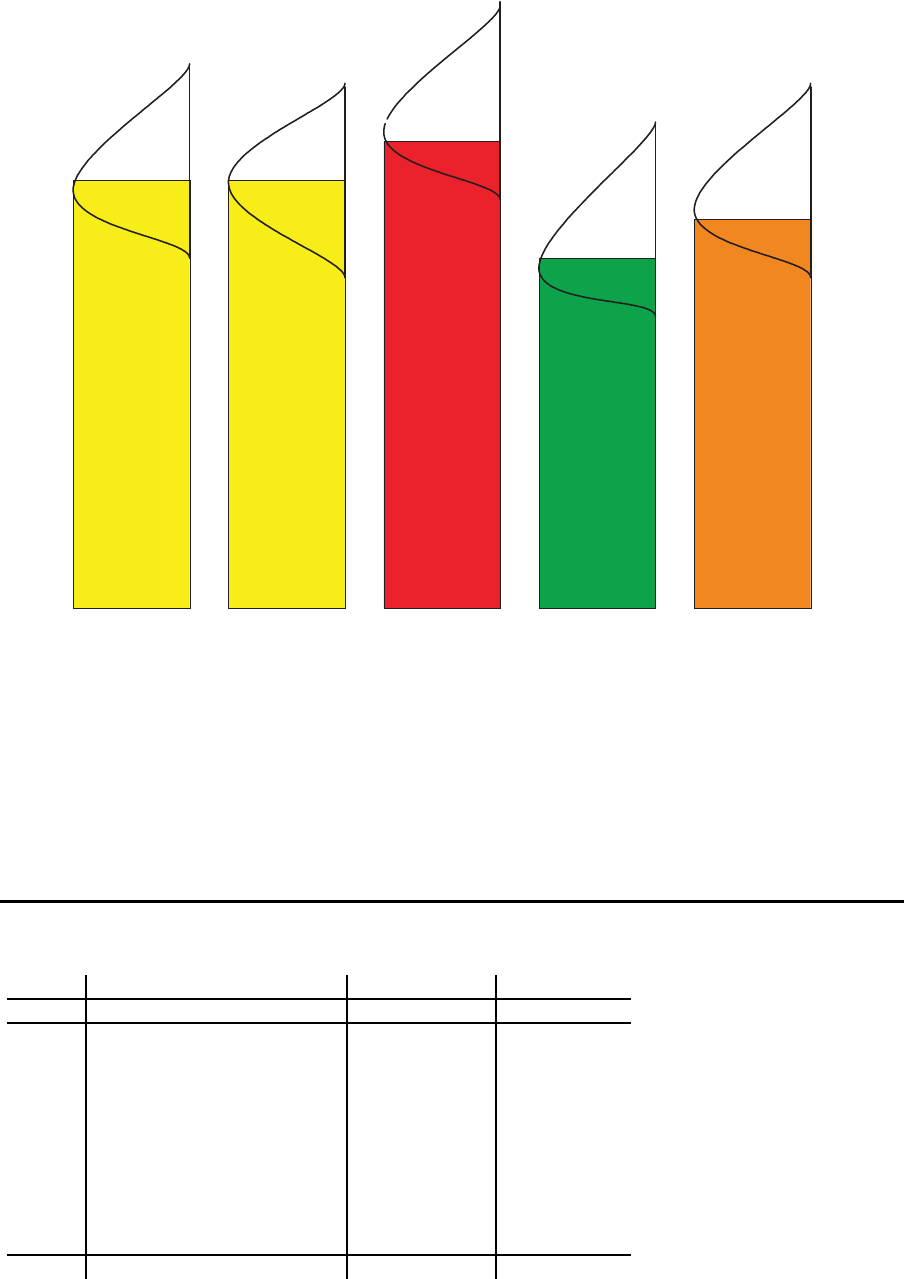
Ungleichm¨aßige Mittelwerte
unbalanced flowline
Arbeitslast
Stationen
Station 1:
33 Sekunden
Station 2:
33 Sekunden
Station 3:
36 Sekunden
Station 4:
27 Sekunden
Station 5:
30 Sekunden
Nicht-identische mittlere Sta tionszeiten der Stationen sind in der Praxis die Regel. Die
Stationszeiten sind ja das Ergebnis einer Fl i eßbandabstimmung. Dabei gelingt es wegen
der Unteilbarkeit der Arbeitselemente i. d. R. nicht, ein Ergebnis mit identischen Station-
szeiten zu ermitteln.
Beispiele aus der Praxis finden Sie hier:
http://www.pom-consult.de/POMConsult/POMFlowe/Hm00000385.Html
Mehrere Produktarten
Var iante
Station 1 2 3 4 5 E{X} E{X
2
} Varianz CV
1 9 11 8 11 9 9.6 93.6 1.44 0.13
2 8 10 9 8 8 8.6 74.6 0.64 0.09
3
10 9 11 9 11 10 100.8 0.8 0.09
4 11 8 9 10 10 9.6 93.2 1.04 0.11
5 8 8 10 9 9 8.8 78 0.56 0.09
6
9 11 9 10 8 9.4 89.4 1.04 0.11
7 11 10 8 8 11 9.6 94 1.84 0.14
8 8 8 11 10 8 9 82.6 1.6 0.14
9
9 9 8 11 9 9.2 85.6 0.96 0.11
10 11 10 11 8 11 10.2 105.4 1.36 0.11
9.4 9.4 9.4 9.4 9.4
48
Sind die Stationen eines Fließproduktionssystemen so flexib el, daß sie Varianten eines
Grundprodukts ohne einen Umr¨ustvorgang in wahlfreier Reihenfolge bearbeiten k¨onnen,
dann kann man die Bearbeitungszeit an einer Station als gewogenen Durchschnitt der
Bearbeitungszeiten der einzelnen Varianten modellieren. Selbst dann, wenn die indi-
viduellen Bearbeitungszeiten der Werkst¨ucke deterministisch sind, kann man die Bear-
beitungszeiten aus der Sicht einer Station als Zufallsvariable auffassen. Diese Vorge-
hensweise hat sich auch b ei der Analyse Flexibler Fertigungssysteme bew¨ahrt.
St¨orungen
0.5
0.6
0.7
0.8
0.9
1.0
Produktionsrate
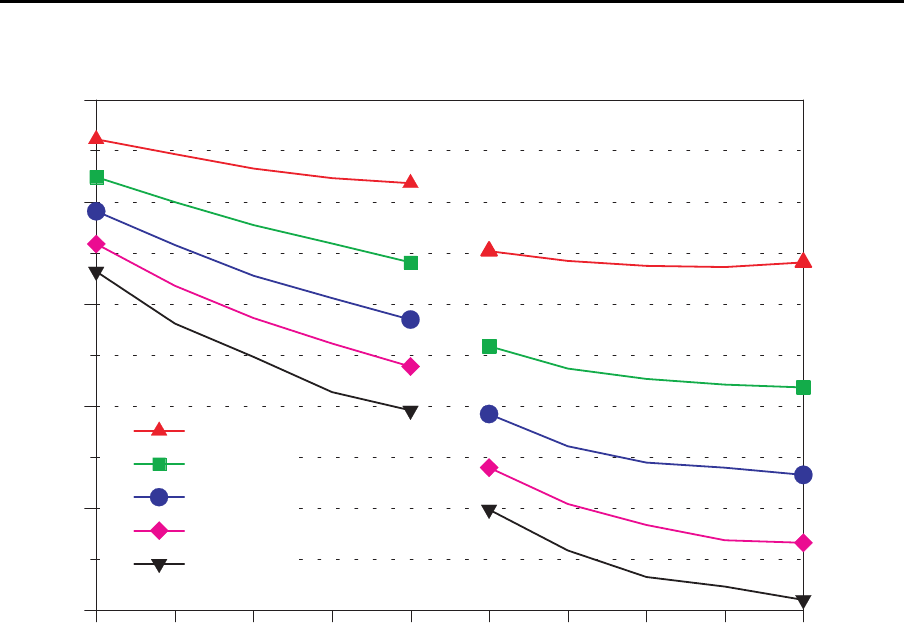
1 2 3 4 5 1 2 3 4 5
mittlere Reparaturzeit
V=0.98
V=0.96
V=0.94
V=0.92
V=0.90
Puffer=4
Puffer=0
St¨orungen k¨onnen zahlreiche Ursachen haben: Werkzeugbruch, Maschinenausf¨alle, Prob-
leme mit der Zuf¨uhrung von Teilen in der Monta ge, etc. St¨orung en k¨onnen zeitabh¨angig
oder nutzungsabh¨a ngig sein. Nutzungsabh¨angige St ¨orungen treten nur w¨ahrend der Bear-
beitung auf (z. B. Werkzeugbruch). Zeitabh¨angige St ¨orungen k¨onnen immer auftreten,
z. B. bei einem Antrieb einer Maschine, die sich im Leerlauf befindet.
Oft wird in analytischen Modellen zur Leistungsanalyse angenommen, daß die Abst¨ande
zwischen Ausf¨allen einer Exponentialverteilung folgen. Auch die Weibullverteilung oder
die Erlang-Verteilung werden – vor allem in der Praxis bei der Anwendung von Simula-
tionsmodellen zur Leistungsanalyse – oft angenommen.
Man muß i. a. eine theoretische Verteilung unterstellen, da der Planer i. d. R. nur sehr
wenig Informationen ¨uber die St¨orungscharakteristika einer Maschine hat. Maschinen-
hersteller geben oft nur die mittlere st¨orungsfreie Laufzeit (MTTF) an. Die Reparaturzeit
h¨angt aber von der Art der St¨orung und der Organisation des Entst¨orprozesses ab.
Die Reparaturzeiten erh¨ohen die Zeitspanne, w¨ahrend der eine Station durch ein Werk-
49

st¨uck belegt ist. Man nimmt oft an, daß die Reparaturzeiten aufgrund der verschiedenen
unterschiedlichen St¨oreinfl¨usse, die aufgetreten sein k¨onnen, sehr großen Schwankungen
unterliegen. In vielen F¨allen wird f¨ur die Reparaturzeiten eine Exponentialverteilung
angenommen.
Zur Veranschaulichung des Einflusses der St¨orungen auf die Produktionsrate eines FPS
betrachten wir ein System mit zehn identischen vollautomatisierten Stationen. Die Sta-
tionszeiten (mittlere Bearb eitungszeiten) seien deterministisch und an allen Sta t ionen
einheitlich gleich eins. Die Stationen unterliegen operationsabh¨angigen St¨orungen und
die Puffer sind beschr¨ankt. Die St¨orungen treten mit exponentialverteilten Abst¨anden
mit dem Mittelwert MTTF (mean time to failure) auf. Die Reparaturdauer ist eben-
falls eine exponentialverteilte Zufallsvariable mit dem Mittelwert MTTR (mean time to
repair). Das obige Bild zeigt f ¨ur unterschiedliche Verf¨ugbarkeiten (V =
MT T F
MT T F +M T T R
),
welchen Einfluß die mittlere Reparaturdauer (MTTR) bei variierenden Puffergr¨oßen auf
die Produktionsrate hat.
Produktionsfehler
?
fehlerhaftes
Werkstück
fehlerfreies
Werkstück
Begrenzte Anzahl Werkst¨ucktr¨ager
Entwicklung der Produktionsrate
50
0.0
0.1
0.2
0.3
0.4
0.5
P
r
o
d
u
k
t
i
o
n
s
r
a
t
e
,
X
0 10 20 30 40 50 60 70 80 90 100
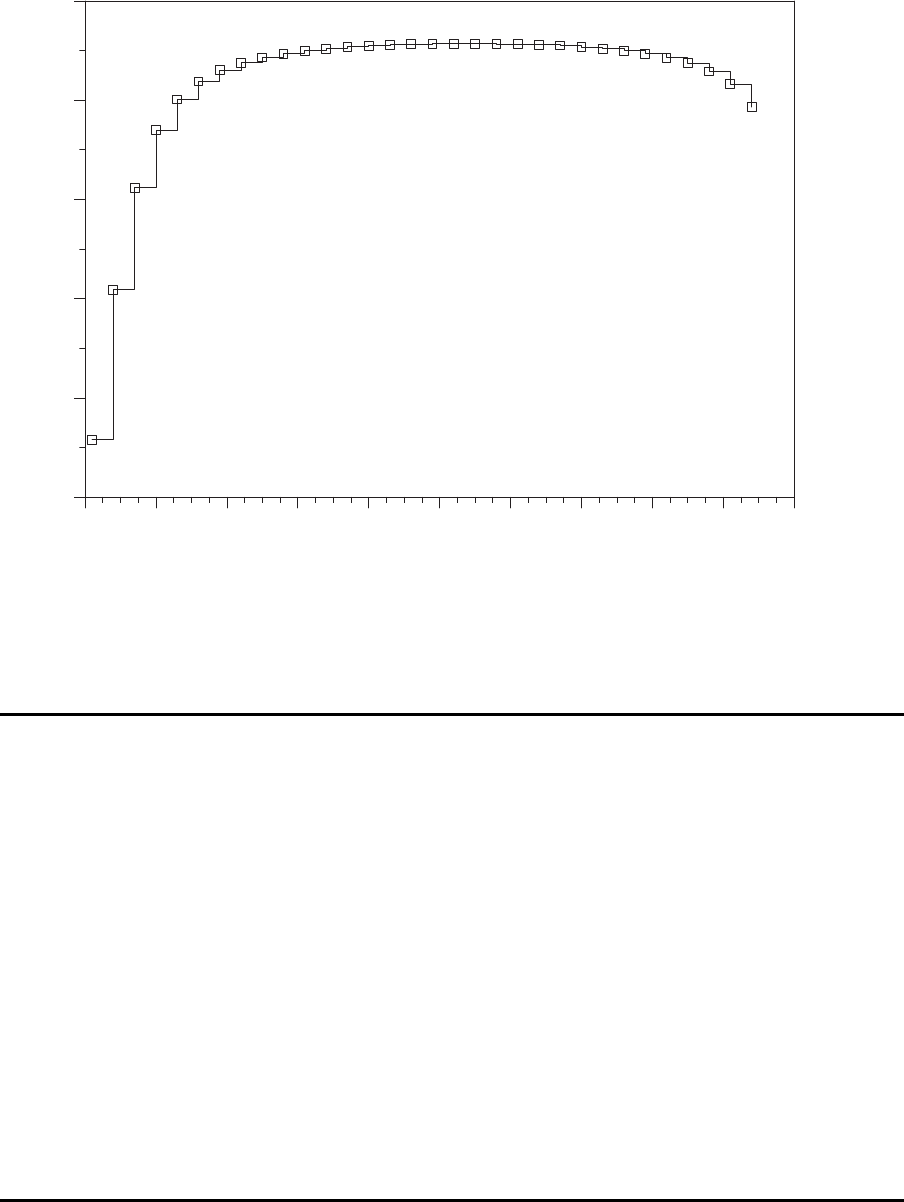
Anzahl Werkstücke, N
Ist bei begrenzten Puffergr¨oßen auch die Anzahl der Werkst¨ucktr¨ager begrenzt, dann
steigt die Produktionsrate mit zunehmender Anzahl Werkst¨ucktr¨ager zun¨achst an, nimmt
dann aber aber irgendwann wieder ab. Wird eine kritische Anzahl ¨uberschritten, dann
kommt das System zum Stillstand, weil sich nichts mehr bewegen kann.
Produktionsverluste
• Blocking
• Starving
Aufgrund der genannten stochastischen Einfl¨usse gelingt es nicht mehr, die Werkst¨ucke
simultan durch das Fließproduktionssystem zu bewegen. Es kommt zu Staus und einige
Station leiden zeitweise unter Materialmangel. Diese Ph¨anomene werden als Blocking
bzw. Starving bezeichnet.
F¨ur die analytische Leistungsanalyse ist es von besonderer Bedeutung, daß es gelingt,
den Anteil dieser Effekte an der Gesamt-Einsatzzeit einer Station gut abzusch¨atzen.
10.2 Systemtypen, Entscheidungsprobleme
Systemtypen
• Systeme mit Bestandskontrolle
51
• Systeme ohne Bestandskontrolle
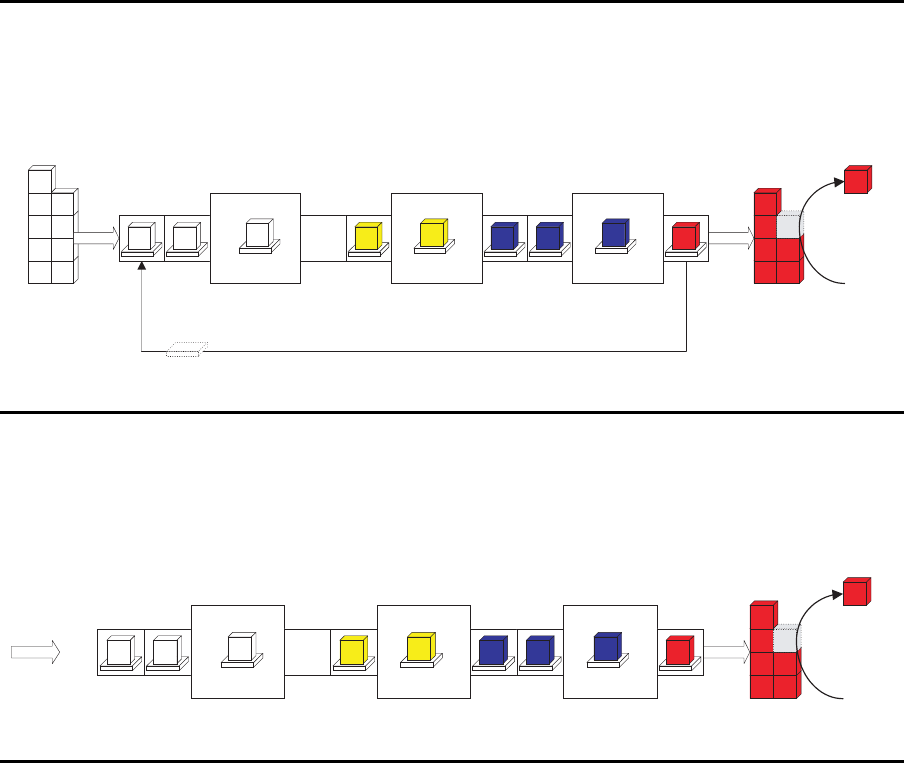
FPS mit Bestandskontrolle
Geschlossene Systeme
Station 1 Station 2 Station 3
Aufträge
Fertigprodukt-
lager
Rohmaterial-
lager
Paletten
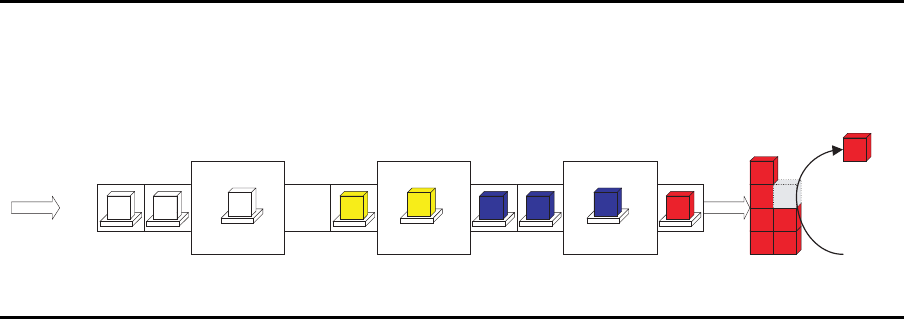
FPS ohne B estandskontrolle
Offene Systeme
Station 1 Station 2 Station 3
Aufträge
Fertigprodukt-
lager
Station 1
Zugangs-
prozeß
Entscheidungsprobleme
1. Art und Anzahl der Produktarten
2. Dimensionierung des Fließproduktionssystems
• Wie viele parallele Linien?
• Anzahl der Stationen pro Linie?
• Verteilung der Arbeitsbelastung auf die Stationen (Fließbandabstimmung)?
• Puffergr¨oßen an den Stationen?
3. Technische Ausstattung des Fließproduktionssystems
• Art des Materialflusses (synchron, asynchron)
• Transp ortsystem (technische Ausgestaltung)
52
11 Fließproduktionssysteme ohn e Bestand skontrolle
Literaturhinweis
G¨unther and Tempelmeier (2016), Abschnitt 7.3.2
FPS ohne B estandskontrolle
Station 1 Station 2 Station 3
Aufträge
Fertigprodukt-
lager
Station 1
Zugangs-
prozeß
Fragen
• Welche Systemkonfigurat ion soll zur Erreichung der angestrebten Produktionsmenge
pro Periode (Produktionsrate) verwendet werden?
• Kann eine betrachtete Systemkonfigura t ion die angestrebte Produktionsmenge pro
Periode (Produktionsrate) erreichen?
53

11.1 Unbeschr¨ankte Puffer, Exponentialverteilung
Einstufiges Warteschlangensystem
Station 1 Station 2 Station M
ankommende
Kunden
Ankunftsrate λ
Wartesystem
Bediensystem
Bedienrate µ
bediente
Kunden
Exponentialverteilt e Bearbeitungszeiten
Annahmen
• M Stationen
• exp onentialverteilte Bearbeitungszeiten
• ausreichend Platz vor jeder Station
Leistungskenngr¨oßen I
• Produktionsmenge
X = λ
• Auslastung
U
m
= λ ·b
m
m = 1, 2, ..., M
54

Leistungskenngr¨oßen II
• Lagerbestand (wartend und in Arbeit)
Q =
M
X
m=1
Q
m
Q
m
=
U
m
1 −U
m
m = 1, 2, ..., M
• Wahrscheinlichkeitsverteilung des Lagerbestands
P
n
m
= 1 −U
m
n
m
= 0; m = 1, 2, . . . , M
P
n
m
= P
0
· U
n
m
m
n
m
≥ 1; m = 1, 2, . . . , M
Leistungskenngr¨oßen III
• Durchlaufzeit
W =
M
X
m=1
W
m
W
m
=
b
m
1 −U
m
m = 1, 2, ..., M
55

11.2 Unbeschr¨ankte Puffer, allgemein verteilte Zeiten
Literaturhinweis
Tempelmeier (2018), Aufgabe A3.4
Aufgabe
Implementieren Sie die For meln in einem Tabelllenkalkulationsprogramm Ihrer Wahl.
Beispiel
• exp onentialverteilte Ankunftszeiten an Station 1
• gamma-verteilte Bearbeitungszeiten, identisch 10 Minuten f¨ur alle Stationen, CV
2
b
=
0.04 bzw. CV
b
= 0.2
m CV
2
a
CV
2
d
E{L
m
} Sim E{W
m
} Sim
1 1.000 0.361 2.403 2.344 30.032 29.348
2 0.361 0.131 1.380 1.213 17.245 15.170
3 0.131 0.049 1.012 1.098 12.647 13.726
4 0.049 0.019 0.879 1.039 10.993 13.025
5 0.019 0.008 0.832 1.035 10.398 12.960
6.506 6.729 81.315 84.229
Aufgabe
Falls Sie Arena beherrschen: Entwickeln Sie ein Arena-Simulationsmodell des betra-
chteten Fließproduktionssystems.
Einfluß der St reuung der Bearbeitungszeiten
auf die Durchlaufzeit
56
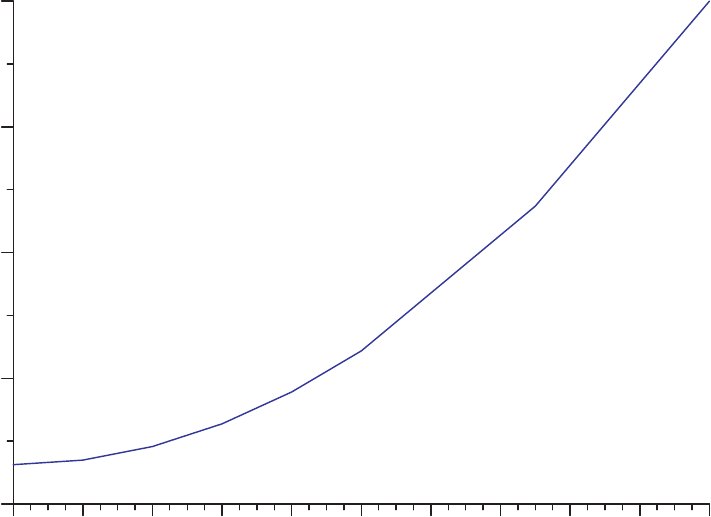
100
200
300
400
500
Durchlaufzeit
0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
Variationskoeffizient der Bearbeitungszeit
(identische Stationen)
10 identische Stationen
poisson-verteilte Ankünfte (0.08 pro Minute)
allgemein verteilte Bearbeitungszeiten
57