9
Teil XVII
Operative Planung bei
Zentrenproduktion
45 Einf¨uhrung
Siehe auch Tempelmeier and Kuhn (1993), Abschnitt 5.
G¨unther and Tempelmeier ( 2016), Abschnitt 9.3
Stichworte Komplexit¨at des Problems; Daten; Entscheidungsvariablen; Zerlegung des Prob-
lems;
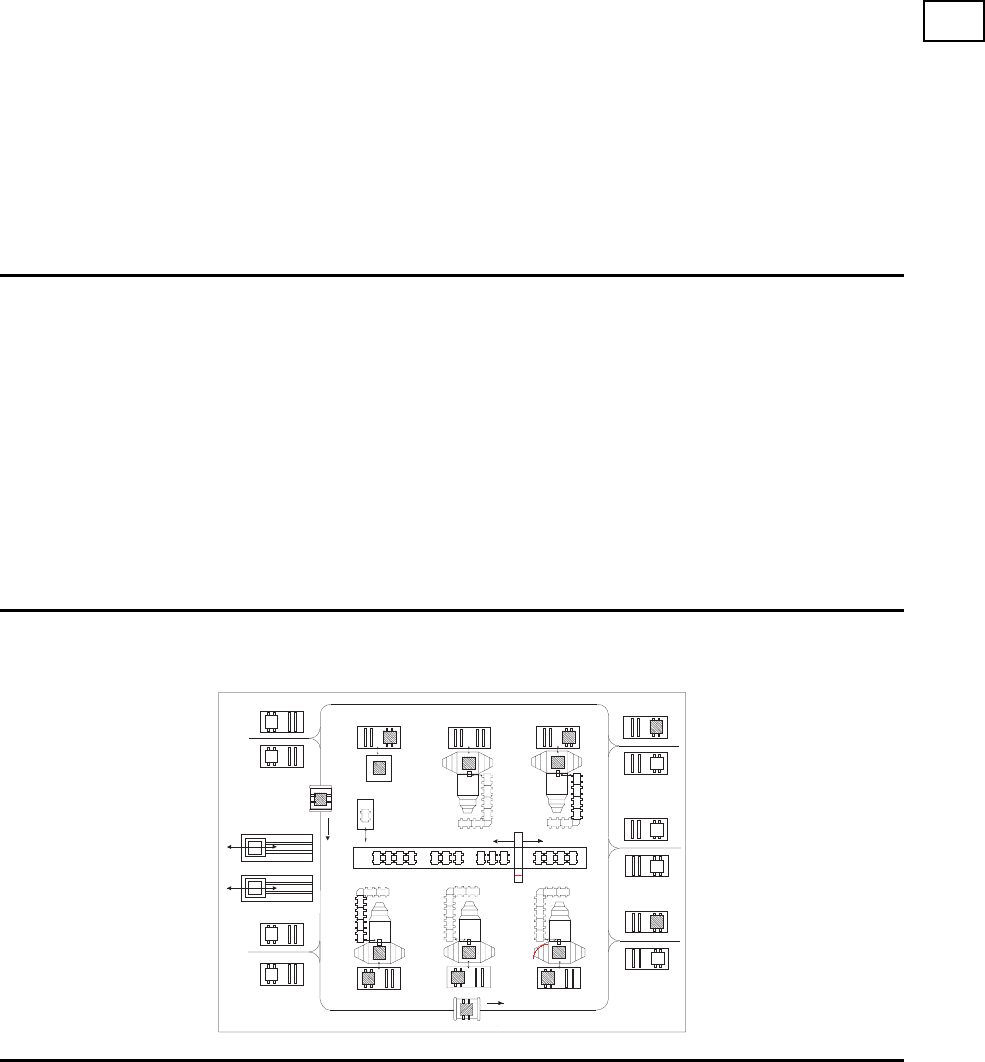
Flexibles Fertigungssystem
Spannstation
fahrerloses Transportsystem
zentraler
Palettenspeicher
Werkzeugmagazin
Werkzeug-
einstellung
Flexibles Fertigungssystem: Merkmale
• geringe Umr¨ustzeitverluste
• begrenzte Anzahl Werkst¨ucke
• flexible Wege der Werkst¨ucke
274
• begrenzte Palettenanzahl
• Spannvorrichtungen
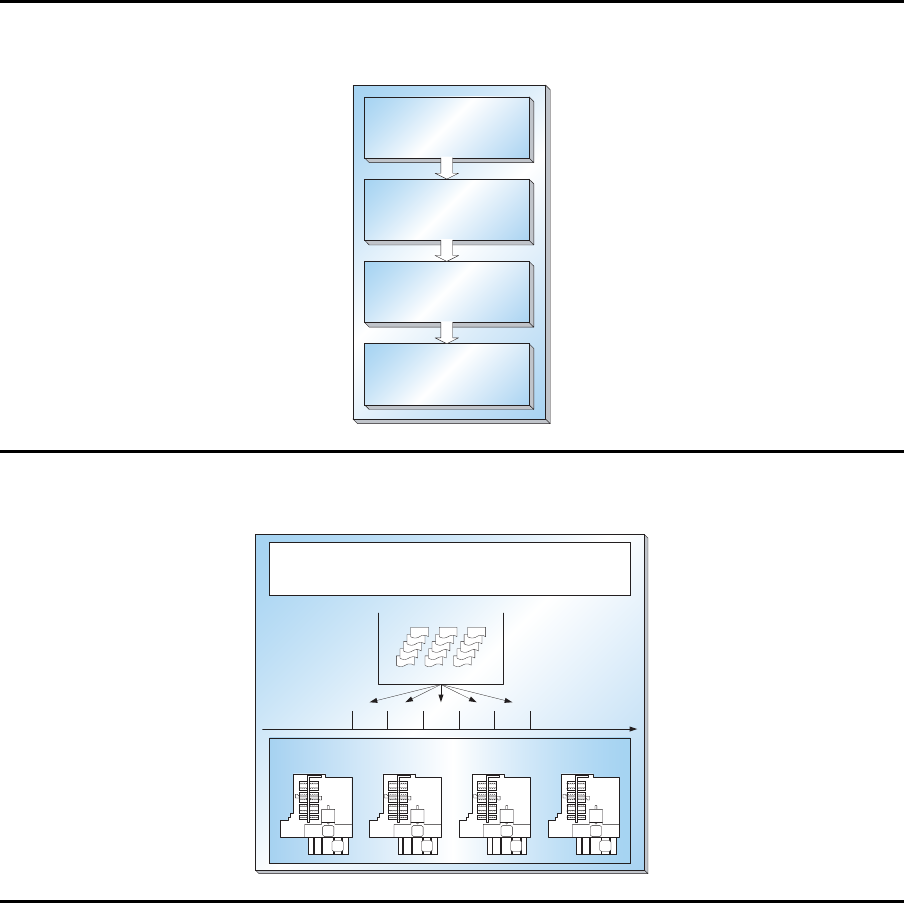
Einlastungsplanung
Verfügbarkeitsprüfung
Serienbildung
Systemrüstung
(Werkzeugmagaz ine,
Spannelemente)
Reihenfolgeplanung
Serienbildung
FFS
12345
Produktionsplanung und -steuerung
Auftrags-
bestand
Serien
Systemr¨ustung
275
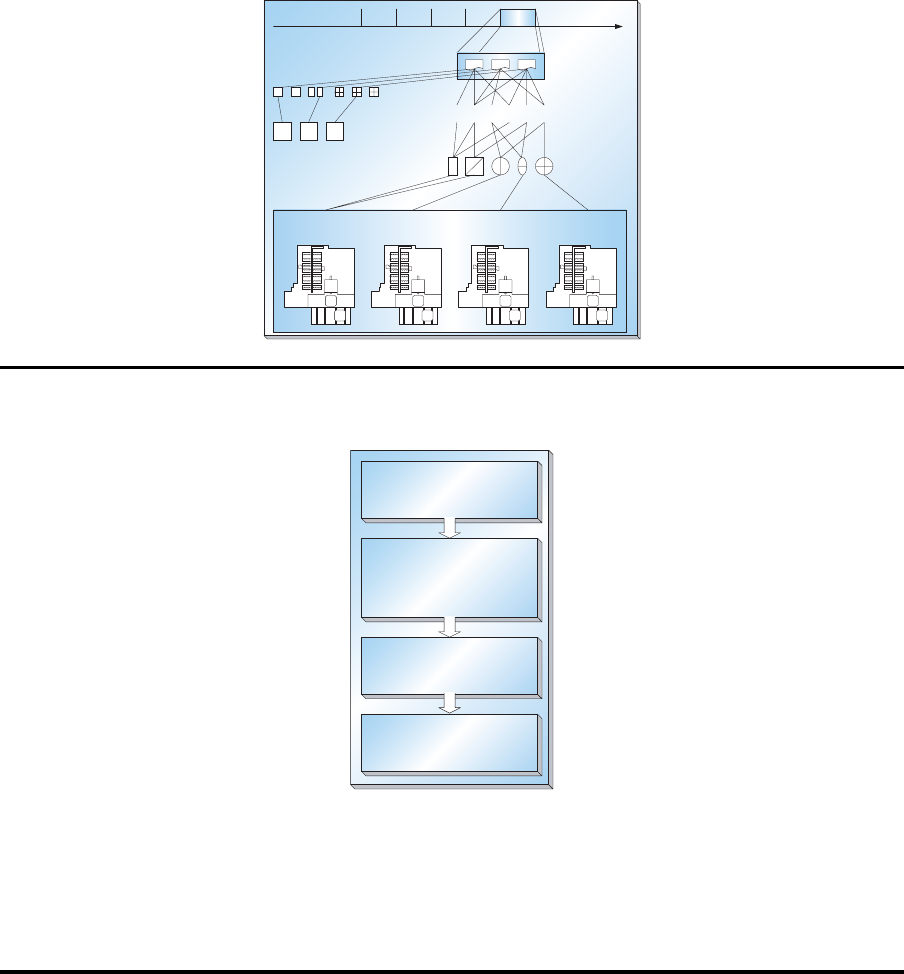
2345
Serien
FFS
Aufträge
Arbeitsgänge
Werkzeuge
Paletten
Spannvorrichtungen
a b c d e
f
1
Steuerung
Auftragsfreigabe
Ablaufsteuerung
-Arbeitsgang
-Arbeitsgang/Maschine
-Fahrzeuge
Betriebsmittel-
überwachung
Auftrags-
überwachung
46 Serienbildun g
46.1 Grundmodell
Annahmen
• Auftragsmenge mit J (j = 1, 2, ..., J) Auft r¨agen
• Auftrag j umfaßt n
j
identische Werkst¨ucke
• Das FFS besteht aus M erg¨anzenden Maschinen.
• Arbeitsplan
• Bearbeitungszeit eines Werkst¨ucks des Auftrags j an Maschine m: b
jm
• Werkzeuge; Gesamtwerkzeugmenge von T Werkzeugen
276

• Werkzeugmagazinkapazit¨at: h
m
Das Entscheidungsmodell zur Serienbildung bei Einlastung statisch fester Serien wird nun
unter Ber¨ucksichtigung der Zielsetzung ”‘Minimiere die Serienanzahl” wie folgt beschrieben:
Modell SEF – Grundmodell der Serienbildung I
Min Z
l
= L (21)
u. B. d. R.
L
X
l=1
x
jl
= 1 j = 1, 2, ..., J (22)
J
X
j=1
σ
jtm
· x
jl
≤ J · y
tml
t = 1, 2, ..., T ; m = 1, 2, ..., M; l = 1, 2, ..., L (23)
T
X
t=1
σ
t
· y
tml
≤ h
m
m = 1, 2, ..., M; l = 1, 2, ..., L (24)
x
jl
∈ {0, 1} j = 1, 2, ..., J; l = 1, 2, ..., L (25)
y
tml
∈ {0, 1} t = 1, 2, ..., T ; m = 1, 2, ..., M; l = 1, 2, ..., L (26)
Symbole
Daten
j Index der Auftr ¨age (j = 1, 2, ..., J)
l Index der Serien (l = 1, 2, ..., L)
m Index der Maschinen (m = 1, 2, ..., M)
t Index der Werkzeuge (t = 1, 2, ..., T )
h
m
Werkzeugmagazinkap azit¨at der Maschine m
σ
t
Anzahl der Werkzeugmagazinpl¨atze, die Werkzeug t ben¨otigt
σ
jtm
(
1 falls Auftrag j an Maschine m Werkzeug t ben¨otigt
0 sonst
Die Beziehung (21) beschreibt die Zielsetzung der Minimierung der Serienanzahl. Je
geringer die Anzahl der Serien ist, umso seltener wird eine Neubelegung der Werkzeug-
magazine an den Maschinen erforderlich. Je k¨urzer die Zykluszeit der Auftrag smenge ist,
umso eher steht das FFS wieder zur Bearbeitung weiterer Auftr¨age zur Verf¨ugung. Die
Nebenbedingungen (22) gew¨ahrleisten, daß jeder Auftrag j (j = 1, 2, ..., J) genau einer
Serie l zugeordnet wird (vollst¨andige Serienbildung). Die Nebenbedingungen (23) stellen
sicher, daß die jeweils ben¨o tigten Werkzeuge a n den Maschinen bereitgestellt werden. Das
begrenzte Fassungsverm¨ogen der Werkzeugmagazine an den Maschinen wird ¨uber die Be-
dingungen (24) abgebildet. Die Gleichungen (25) und (26) definieren die Wertebereiche
der Variablen.
277

Symbole
Variablen
L Anzahl der Serien
y
tml
(
1 falls Werkzeug t der Maschine m f¨ur die Serie l zugeordnet wird
0 sonst
x
jl
(
1 falls Auftrag j der Serie l zugeordnet wird
0 sonst
46.2 Das Modell von Hwang
Aufbauend auf der inversen Beziehung zwischen Seriengr¨oße und Serienanzahl bei gegebener
Anzahl von Auftr¨agen strebt Hwang die Minimierung der Serienanzahl durch Max-
imierung der Anzahl der Auftr¨age bzw. Werkst¨ucke in einer Serie an. Er formuliert das
folgende bin¨are lineare Modell, welches er in einem iterativen Verfahren mehrfach auf
eine schrittweise sich verkleinernde Restmenge jeweils noch nicht eingeplanter Auft r ¨age
J
0
solange anwendet, bis alle Auftr¨age einer Serie zugeordnet worden sind.
Modell Hwang
Max Z
l
=
X
j∈J
0
x
jl
| {z }
Anzahl der Auftrage in
der aktuell betrachteten
Serie
(27)
u. B. d. R.
X
j∈J
0
σ
jtm
· x
jl
≤ J · y
tm
t = 1, 2, ..., T ; m = 1, 2, ..., M (28)
T
X
t=1
σ
tm
· y
tm
≤ h
m
m = 1, 2, ..., M (29)
x
jl
= {0, 1} j ∈ J
0
(30)
y
tm
= {0, 1} t = 1, 2 , ..., T ; m = 1, 2, ..., M (31)
Das Modell SEFHWANG w¨ahlt aus der Menge J
0
der zu Beginn einer Iteration noch
nicht eingeplanten Auftr¨age eine Teilmenge J
l
aus und faßt diese zu einer Seriel zusam-
men. Mit der Zielfunktion (27) wird die Anzahl der Auftr¨age in der aktuell betrachteten
Serie l maximiert. Die Nebenbedingungen (28) sorgen daf¨ur, daß die jeweils ben¨otigten
Werkzeuge an den Maschinen bereitgestellt werden. Falls ein Auftrag j in die Serie l
278

aufgenommen wird, der das Werkzeug t an Maschine m ben¨otigt, muß dieses Werkzeug
in das Werkzeugmagazin an der Maschine aufgenommen werden. Die Begrenzung des
Fassungsverm¨ogens der Werkzeugmagazine an den Maschinen wird ¨uber die Bedingun-
gen (29) abgebildet. Das Modell SEFHWANG wird im Rahmen des unten beschriebenen
Verfahrens mehrfach solange angewendet, bis die Menge der noch nicht einer Serie zuge-
ordneten Auftr¨age leer ist.
Symbole
Daten
j Index der Auftr ¨age (j = 1, 2, ..., J)
l Index der Serien (l = 1, 2, ..., L)
m Index der Maschinen (m = 1, 2, ..., M)
t Index der Werkzeuge (t = 1, 2, ..., T )
h
m
Werkzeugmagazinkap azit¨at der Maschine m)
J
0
Menge der Auftr¨age, die noch keiner Serie zugeordnet wurden
σ
tm
Anzahl der Werkzeugmagazinpl¨atze, die Werkzeug t an Maschine m
ben¨otigt)
σ
jtm
(
1 falls Auftrag j an Maschine m Werkzeug t ben¨otigt
0 sonst
Symbole
Variablen
y
tm
(
1 falls Werkzeug t der Maschine m zu geordnet wird
0 sonst
x
jl
(
1 falls Auftrag j der Serie l zugeordnet wird
0 sonst
Verfahren von Hwang
a) Initialisiere J
0
= Menge aller Auftr¨age
b) L ¨ose das Modell SEF-HWANG f¨ur die Auftragsmenge J
0
. Die Menge der Auftr¨ag e,
die der aktuellen Serie l zugeordnet wurden, ist J
l
.
c) Aktualisiere J
0
:= J
0
\J
l
. Falls die Menge J
0
nicht leer ist, gehe zu Schritt a).
Aufgrund der sukzessiven Vorgehensweise des Verfahrens HWANG besteht die Gefahr,
daß lediglich L¨osungen geringer Qualit¨at gefunden werden, da Auftr¨age mit niedrigem
Werkzeugbedarf in den ersten Iterationen bevorzugt ausgew¨ahlt und einer Serie zugeord-
net werden, w¨ahrend Auftr¨age mit hohem Werkzeugbedarf erst am Ende des Verfahrens
279
eingeplant werden. Im Falle eines dynamischen Auftragsankunftsprozesses kommen die
Auftr¨age mit großem Werkzeugbedarf unter bestimmten Umst¨anden ¨uberhaupt nicht zum
Zuge.
Zur Vera nschaulichung betrachten wir ein Beispiel. Wir betrachten eine Maschine, deren
Werkzeugmagazin eine Kapazit¨at von h
m
= 8 Werkzeugen hat. Es sind J = 10 Auftr¨age
einzuplanen. Insgesamt werden dabei T = 21 Werkzeuge ben¨otigt. Die folgende Tabelle
zeigt den Werkzeugbedarf der einzelnen Auftr¨age.
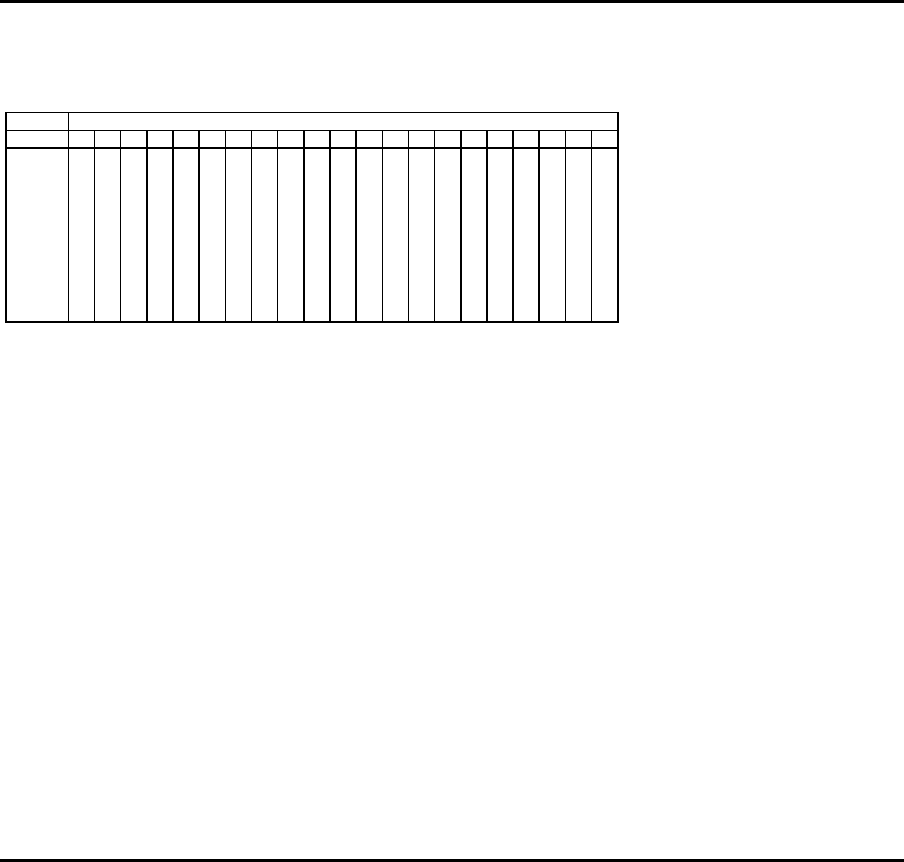
Beispiel
Werkzeugbedarfe der Auftr¨age
Werkzeug
Auftrag 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
1 X X X
2 X X X X
3 X X X X X X
4 X X X X
5 X X X X X
6 X X X X X X
7 X X X
8 X X X X X
9 X X
10 X X X X
Nach dem Verfahren von Hwang wird in der ers ten Iteration zun¨achst das Modell SEFH-
WANG unter Ber¨ucksichtigung aller Auftr¨age f ormuliert.
Die optimale L¨osung dieses bin¨aren linearen Optimierungsproblems lautet: x
1
= 1, x
2
=
1, x
7
= 1, x
9
= 1. Daher wird die erste Serie aus den Auftr¨agen 1, 2, 7 und 9 gebildet.
Zur Vorbereitung der zweiten Iteration des Verfahrens werden diese Auftr¨age aus der
Menge der noch einzuplanenden Auftr¨age entfernt. Die optimale L¨osung des resultieren-
den bin¨aren Optimierungsproblems lautet: x
5
= 1, x
10
= 1. Die zweite Serie umfaßt
damit die Auftr¨age 5 und 10. Die in der dritten Iteration gebildete Serie umfaßt die
Auftr¨age 4 und 6. Die Serien 4 und 5 schließlich enthalten mit den Auftr¨agen 3 bzw. 8
jeweils nur noch einen Auftrag.
Die Struktur der auf diese Weise gebildeten Serien und die Nummern der jeweils durch
die Auft r¨age einer Serie ben¨otigten Werkzeuge sowie die daraus resultierende Belegung
der Pl¨atze des Werkzeugmagazins zeigt folgende Tabelle. Der ersten Serie werden die
Werkzeuge 6, 12, 15, 16, 20, 9, 14 und 10 zugeordnet. Ein Stern ”*” markiert, daß das
f¨ur den betrachteten Auftrag ben¨otigte Werkzeug bereits f¨ur einen anderen Auftrag in
das Werkzeugmagazin aufgenommen worden ist und daher kein zus¨atzlicher Maga zinplatz
ben¨otigt wird.
Verfahren von Hwang – Beispiel II
L¨os ung
280

Magazinplatz
1 2 3 4 5 6 7 8
Serie 1 Auf trag 2 6 12 15 16
Auftrag 7 * * 20
Auftrag 1 * 9 14
Auftrag 9 * 10
Serie 2 Auf trag 10 2 4 14 18
Auftrag 5 * 5 9 8 13
Serie 3 Auf trag 6 1 3 7 13 17 21
Auftrag 4 * * 6 19
Serie 4 Auf trag 3 5 6 11 12 17 20
Serie 5 Auf trag 8 2 8 13 16 21
* Werkzeug bereits vorhanden
47 Systemr¨ustung
47.1 Einf¨uhrung
Systemr¨ustung
Zielsetzungen
• Minimierung der entscheidungsrelevanten Kosten
• Minimierung der Abweichungen zwischen Plan- und Ist-Auslastung
• Minimierung der maximalen Maschinenbelastung
• Minimierung der Anzahl bereitzustellender Werkzeuge
Systemr¨ustung
Modelle
• Modelle ohne Werkzeugrestriktionen,
• Modelle mit vereinfachten Werkzeugrestriktionen und
• Modelle mit Werkzeugrestriktionen unter Ber¨ucksichtigung gemeinsamer Werkzeugnutzung
• Modelle mit einfacher Werkzeugbelegung und
• Modelle mit mehrfacher Werkzeugbelegung
281

47.2 Keine Werkzeugrestriktionen
Im einfachsten Fall kann das Problem der Arbeitsgang/Maschinen-Zuordnung unter Ver-
nachl¨assigung der sich aus den begrenzten Werkzeugmagazinen ergebenden Restriktionen
als verallgemeinertes Zuordnungsproblem dargestellt werden. Kusiak formuliert ein de-
rartiges Modell f¨ur den Fall, daß die zeitliche Kapa zit¨at der Maschinen des FF-Systems
beschr¨ankt ist und daß durch die Zuordnung eines Arbeitsgangloses o zu einer Maschine
m variable K osten c
om
entstehen.
Modell AGMA-KUS1
Zuordnung von Arbeitsg¨angen zu Maschinen
Min Z =
O
X
o=1
M
X
m=1
c
om
· π
om
(32)
u. B. d. R.
O
X
o=1
b
om
· π
om
≤ g
m
m = 12, ..., M (33)
M
X
m=1
π
om
= 1 o = 12, ..., O (34)
π
om
∈ {0, 1} m = 1, 2, ..., M; o = 12, ..., O (35)
Symbole
m Index der Maschinen (m = 1, 2, ..., M)
o Index der Arbeitsganglose (o = 1, 2, ..., O)
b
om
Bearbeitungszeit des Arbeitsgangloses o an Maschine m
c
om
variable Kosten der Bearbeitung des Arbeitsgangloses o an Maschine m
g
m
zeitliche Kapazit¨at der Maschine m (Zeiteinheiten)
π
om
=
(
1 wenn Arbeitsganglos o an der Maschine m bearbeitet wird,
0 sonst.
Die Zielfunktion (32) beschreibt die mit einer Arbeitsgang/Maschi”-nen-Zuordnung ver-
bundenen Kosten. Die Nebenbedingungen (33) stellen sicher, daß die zeitliche Belastung
einer Maschine m durch die ihr zugeordneten Arbeitsganglose die im Planungszeitraum
verf¨ugbare zeitliche Kapazit¨at der Maschine nicht ¨uberschreitet. Die Gleichungen (34)
gew¨ahrleisten, daß jeder Arbeitsgang genau einer Maschine zugeordnet wird.
Zur L¨osung verallgemeinerter Zuordnungsprobleme, die zur Gruppe der kombinatorischen
Probleme z¨ahlen, existiert eine Reihe von exakten und heuristischen Verfahren. Bei
geringen Problemdimensionen kann das Modell AGMA-KUS1 jedoch auch mit Hilfe eines
Standard-Algorithmus zur bin¨ar en Optimierung gel¨ost werden. Betrachten wir Beispiel
282
mit 2 Maschinen und 8 Arbeitsganglosen, dessen Daten in Tabelle ?? zusammengestellt
sind. Bei gleichen Kapazit¨aten und Bearbeitungszeiten unterscheiden sich die beiden
Maschinen lediglich durch die variablen Kosten.
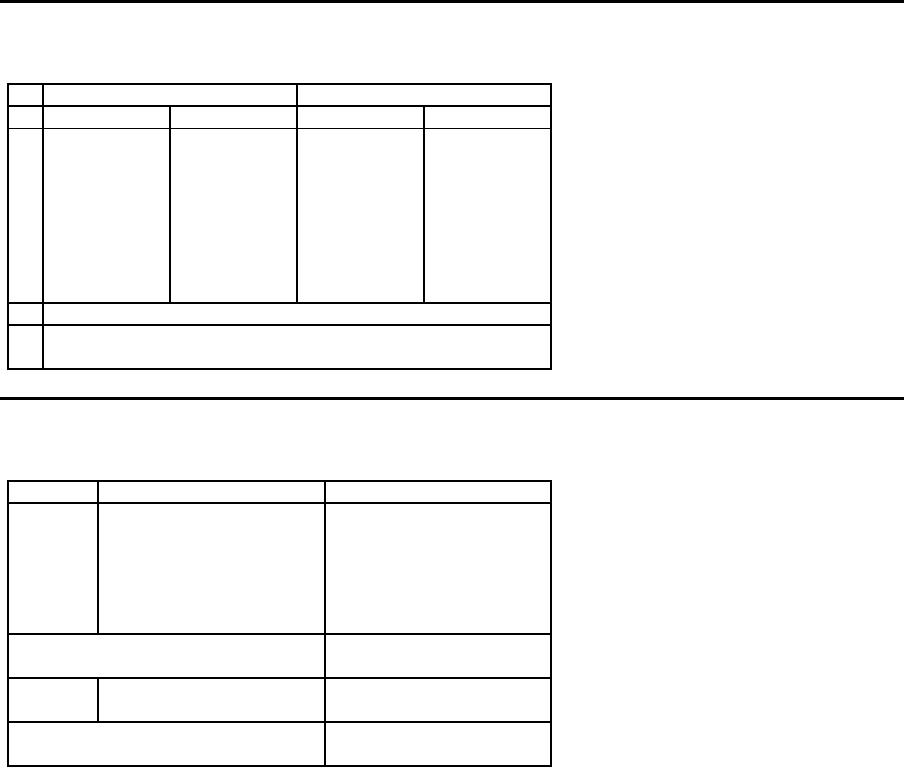
Beispiel zum Modell AGMA-KUS1
Kosten Bearbeitungszeit
o c
o1
c
o2
b
o1
b
o2
1 1 2 30 30
2 1 2 12 12
3 1 2 20 20
4 1 2 9 9
5 1 2 16 16
6 1 2 2 2
7 1 2 17 17
8 1 2 26 26
m Maschinenkapazit¨at g
m
1 80
2 80
L¨osung
Maschine Arbeitsg¨ange Bearbeitungszeiten
1 2 12
3 20
4 9
5 16
6 2
7 17
genutzte Kapazit¨at 76
freie Kapazit¨at 4
2 1 30
8 26
genutzte Kapazit¨at 56
freie Kapazit¨at 24
Die praktische Anwendung des Modells AGMA-KUS1 wirft mehrere Probleme auf. So
sind die Ko sten der Zuordnung eines Arbeitsgangloses o zu jeder Maschine m, c
om
, zu
ermitteln. Die Bestimmung variabler Maschinennutzungsko sten in einem FF-System ist
jedoch i. d. R. ¨außerst schwierig. Die Gr¨oße com darf nur die direkt vo n der Zuordnung
eines Arbeitsgangs zu einer Maschine abh¨ang igen Kosten umfassen. In der industriellen
Praxis wird h¨aufig mit Maschinenstundens¨atzen gerechnet, in denen b ereits proportional-
isierte Gemeinkosten enthalten sind. Diese Kostens¨atze sind f¨ur das Modell AGMA-KUS1
unbrauchbar. F ¨ur ein FF-System wird man i. a. feststellen, daß die entscheidungsrele-
vanten K osten com f¨ur alle ersetzenden Maschinen gleich sind. Dann sind aber auch
alle zul¨assigen L¨osungen des Modells AGMA-KUS1 im Hinblick auf die Zielfunktion gle-
ich gut. Weiterhin muß f¨ur jede Maschine eine zeitliche Kapazit¨atsgrenze g
m
extern
vorgegeben werden. Dies setzt eine Planungsperiode bekannter L¨ange voraus.
283
47.3 Vereinfachte Werkzeugrestriktionen
Vereinfachte Werkzeugrestriktionen
O
X
o=1
σ
o
· π
om
≤ h
m
m = 1, 2, ..., M
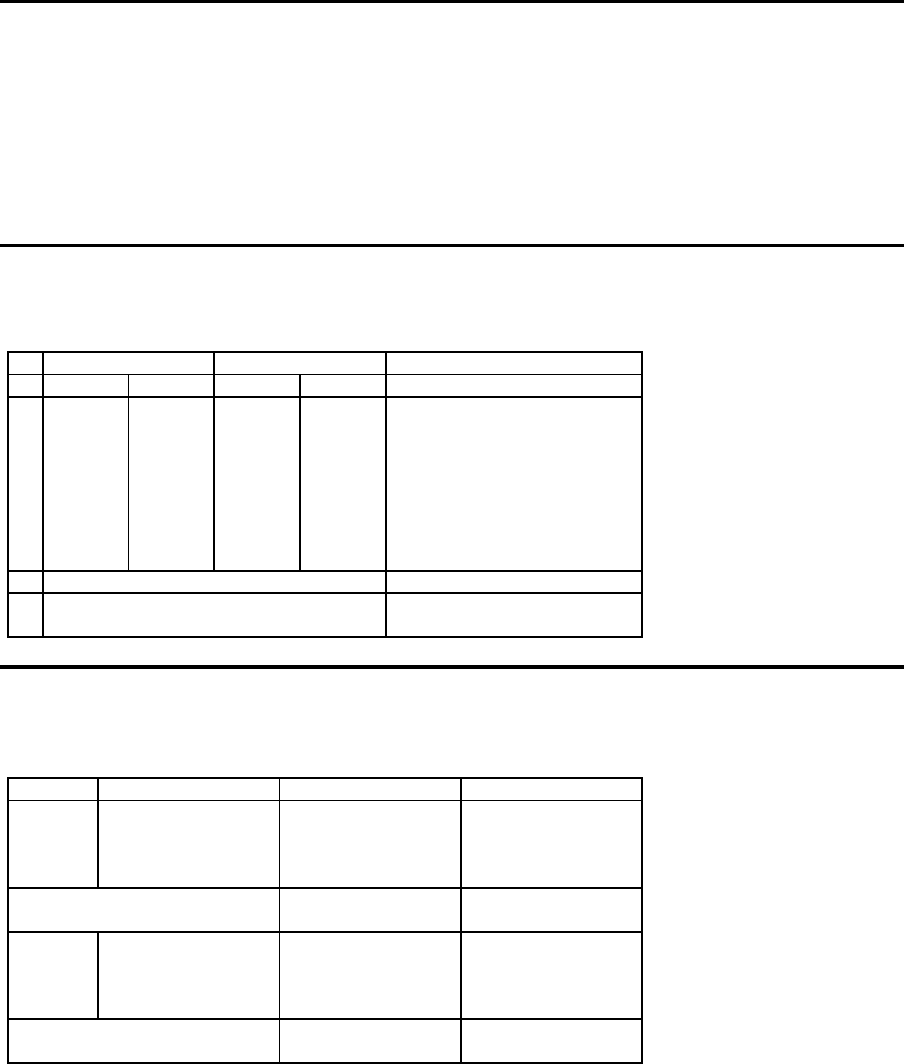
Beispiel
Daten
Kosten Bearbeitungszeit Werkzeugbedarf
o c
o1
c
o2
b
o1
b
o2
σ
o
1 1 2 30 30 5
2 1 2 12 12 6
3 1 2 20 20 4
4 1 2 9 9 10
5 1 2 16 16 3
6 1 2 2 2 10
7 1 2 17 17 4
8 1 2 26 26 5
m Maschinenkapazit¨at g
m
Werkzeugmagazinkapazit¨at h
m
1 80 25
2 80 25
Beispiel
L¨os ung
Maschine Arbeitsg¨ange Bearbeitungszeiten Werkzeuge
1 2 12 6
3 20 4
6 2 10
8 26 5
genutzte Kapazit¨at 60 25
freie Kapazit¨at 20 0
2 1 30 5
4 9 10
5 16 3
7 17 4
genutzte Kapazit¨at 72 22
freie Kapazit¨at 8 3
284

Eine unmittelbare Erweiterung des Modells AGMA-KUS1 entsteht, wenn wir die M¨og-
lichkeit des R¨uckgriffs auf zus¨atzliche Werkzeugkassetten zulassen, die in einem zentralen
Werkzeug-Hintergrundmagazin lagern. In diesem Fall verf¨ugt jede Maschine ¨uber ein
maschinennahes Werkzeugmagazin (mit einer oder mehreren Werkzeugkassetten) mit be-
grenzter Kapazit¨at. Zus¨atzlich k¨onnen w¨ahrend der Bearbeitung unter Inkaufnahme von
Umr¨ustkosten Werkzeugkassetten aus dem Hintergrundmagazin ausgetauscht werden.
Ein Modell, das diesen Tatbestand erfaßt, wird von Kusiak formuliert. Kusiak sieht
zus¨atzlich die M¨oglichkeit vor, daß die Werkst¨ucke eines Arbeitsgangloses mehreren Ma-
schinen zugewiesen werden (Lossplitting). Diese Option wird mit Hilfe von zwei Arten
von Zuordnungsvariablen modelliert. Die ganzzahligen Variablen u
om
definieren die
Anzahl der Werkst¨ucke des Arbeitsgangloses o, die an der Maschine m bear beitet werden
(maschinenbezogene Losgr¨oße). Die bin¨aren Variablen π
om
beschreiben, ob min-
destens ein Werkst¨uck eines Arbeitsgangloses einer Maschine zugeordnet wird oder nicht.
Die simultane Bear beitung mehrerer identischer Werkst¨ucke an unterschiedlichen Maschi-
nen ist nur m¨oglich, wenn mehrere identische Werkzeugs¨atze an verschiedenen Maschinen
bereitgehalten werden.
Modell AGMA-KUS2
I
Min Z =
O
X
o=1
M
X
m=1
c
om
· u
om
+
M
X
m=1
c
m
· z
m
(36)
u. B. d. R.
M
X
m=1
u
om
= n
o
o = 1, 2, ..., O (37)
O
X
o=1
b
om
· u
om
≤ g
m
m = 12, ..., M (38)
O
X
o=1
σ
m
· π
om
≤ h
m
· z
m
m = 12, ..., M (39)
Modell AGMA-KUS2
II
u
om
≤ n
o
· π
om
o = 12, ..., O; m = 1, 2, ..., M (40)
u
om
≥ 0 und ganzzahlig o = 12, ..., O; m = 1, 2, ..., M (41)
z
m
≤ Z
m
und ganzzahlig m = 1, 2, ..., M (42)
π
om
∈ {0, 1} m = 1, 2, ..., M; o = 12, ..., O (43)
285

Symbole
Daten
m Index der Maschinen (m = 1, 2, ..., M)
o Index der Arbeitsganglose (o = 1, 2, ..., O)
σ
o
Anzahl der Werkzeugmagazinpl¨atze, die f¨u r Arbeitsganglos o ben¨otigt
werden
b
om
Bearbeitungszeit des Arbeitsgangloses o an Maschine m
c
m
Umr¨ustkosten f¨ur ein Werkzeugmagazin an Maschine m
c
om
variable Kosten der Bearbeitung des Arbeitsgangloses o an Maschine m
g
m
zeitliche Kapazit¨at der Maschine m (Zeiteinheiten)
n
o
Losgr¨oße des Arbeitsgangloses o
Z
m
Anzahl der Werkzeugmagazine bzw. -kassetten an der Maschine m
Symbole
Variablen
π
om
=
(
1 wenn Arbeitsganglos o an der Maschine m bearbeitet wird,
0 sonst.
u
om
Anzahl der Werks t¨ucke des Arbeitsgangloses o, die an der Maschine m
bearbeitet werden (maschinenbezogene Losgr¨oße)
z
m
Anzahl der ben¨otigten Werkzeugmagazine bzw. -kassetten an Maschine
m
Die Zielfunktion ( 36) minimiert die Summe der von der Zuordnung von Arbeitsg¨angen
zu Maschinen der Arbeitsg¨ange zu den Maschinen abh¨ang igen Kosten einschl. der Um-
r¨ustkosten, die beim Wechseln der Werkzeugmagazine entstehen. Die Gleichungen ( 37)
gew¨ahrleisten, daß alle n
o
Werkst¨ucke eines Arbeitsgangloses bearbeitet, d. h. einer Mas-
chine zugeordnet werden. Die Nebenbedingungen (38) stellen sicher, daß die zeitlichen
Kapazit¨aten der Maschinen nicht ¨uberschritten werden. Die Bedingungen (39) beschr¨a n-
ken die Anzahl der Werkzeuge, die den Werkzeugmagazinen zugeordnet werden k¨onnen
und definieren die Anzahl der notwendigen Werkzeugmagazinwechsel (z
m
). Auf der
linken Seite steht der Werkzeugbedarf an Maschine m, der ent steht, wenn mindestens
ein Werkst¨uck des Arbeitsgangloses o der Maschine m zugeordnet wird. Auf der rechten
Seite wird die Anzahl der verf¨ugbaren Werkzeugpl¨atze beschrieben. Ist z
m
> 1, dann
m¨ussen Werkzeugkassetten an der Maschine m ausgetauscht werden. Die Ungleichun-
gen (40) stellen die Beziehung zwischen den Z uordnungsvariablen π
om
(mindestens ein
Werkst¨uck des Arbeitsganglos o wird an der Maschine m bearbeitet) und der Variablen
uom (maschinenbezogene Losgr¨oße) her.
Zur L¨osung des Modells schl¨agt Kusiak die Anwendung vo n Standard-Algorithmen der
linearen Optimierung (unter Vernachl¨assigung der Ganzzahligkeitsbedingungen) vor. Die
nichtganzzahligen Variablen sollen anschließend auf- bzw. abgerundet werden.
286

47.4 Gemeinsame Werkzeugnutzung
In den bisher diskutierten Modellen zur Arbeitsgang/ Maschinen-Zuordnung wird angenom-
men, daß f¨ur jeden Arbeitsgang, der einer Maschine zugeordnet wird, jeweils ein eigener
Werkzeugsatz in dem Werkzeugmagazin bereitgestellt wird. Dabei bleibt unber¨ucksichtigt,
daß f¨ur unterschiedliche Arbeitsg¨ange teilweise die gleichen Werkzeuge ben¨otigt werden
und es daher oft ausreicht, jeweils nur ein Werkzeug eines Typs in einem Werkzeug-
magazin bereitzustellen.
Die gemeinsame Nutzung eines Werkzeugs durch mehrere Arbeitsganglose kann im Rah-
men der bislang dargestellten LP-Modelle durch die Einf¨uhrung einer weiteren Gruppe
von Bin¨arvariablen erfaßt werden. Bei Ber¨ucksichtigung des Ziels der Minimierung der
maximalen zeitlichen Maschinenbelastung entsteht dann folgendes Modell:
Modell AGMA-KU
Min Z = max
m
{g
m
} (44)
u. B. d. R.
O
X
o=1
b
om
· π
om
− g
m
≤ 0 m = 1, 2, ..., M (45)
T
X
t=1
σ
t
· y
tm
≤ h
m
m = 1, 2, ..., M (46)
O
X
o=1
σ
ot
· π
om
≤ E · y
tm
t = 1, 2, ..., T ; m = 1, 2, ..., M (47)
M
X
m=1
π
om
= 1 o = 1, 2, ..., O (48)
π
om
∈ {0, 1} m = 1, 2, ..., M; o = 12, ..., O (49)
y
tm
∈ {0, 1} t = 1, 2, ..., T ; m = 1, 2, ..., M (50)
Symbole
Daten
m Index der Maschinen (m = 1, 2, ..., M)
o Index der Arbeitsganglose (o = 1, 2, ..., O)
σ
t
Anzahl der Werkzeugmagazinpl¨atze, die f¨ur Werkzeug t ben¨otigt
werden
b
om
Bearbeitungszeit des Arbeitsgangloses o an Maschine m
E große Zahl
σ
ot
=
(
1 wenn Arbeitsganglos o das Wer k zeug t ben¨otigt,
0 sonst.
287

Symbole
Variablen
π
om
=
(
1 wenn Arbeitsganglos o an der Maschine m bearbeitet wird,
0 sonst.
y
tm
=
(
1 wenn Werkzeug t der Maschine m zugeordnet wird,
0 sonst.
g
m
zeitliche Belastung der Maschine m
Die Zielfunktion ( 44) beschr eibt die maximale Maschinenbelastung an den Maschinen,
wobei die realisierten Belastungen durch Beziehung (45) definiert werden. Die Nebenbe-
dingungen (46) beschr¨anken die Anzahl der Werkzeuge, die den Werkzeugmagazinen
zugeordnet werden k¨onnen. Wird Arbeitsganglos o der Maschine m zugewiesen, dann
gew¨ahrleisten die Ungleichungen (47), daß die Bin¨arvariablen y
tm
der zugeh¨origen Werk-
zeuge gleich 1 g esetzt werden und damit auch die notwendige Werkzeugmagazinbelegung
korrekt abgebildet wird. Ist die Varia ble y
tm
aufgrund der Zuordnung eines Arbeits-
gangsloses zu der Maschine gesetzt worden und damit das Werkzeug t an der Maschine
m vorhanden, dann k¨onnen weitere Arbeitsganglose, die ebenfalls das Werkzeug t an
der Maschine m ben¨otigen, auf da s bereits zugeordnete Werkzeug ohne zus¨atzliche Be-
lastung des Werkzeugmagazins zugreifen. Die G leichungen (48) sorgen daf¨ur, daß jeder
Arbeitsgang genau einer Maschine zugeordnet wird.
288