8
42 Einlastungsplanung
42.1 Das ’Mixed-Mod el Sequencing’ Problem
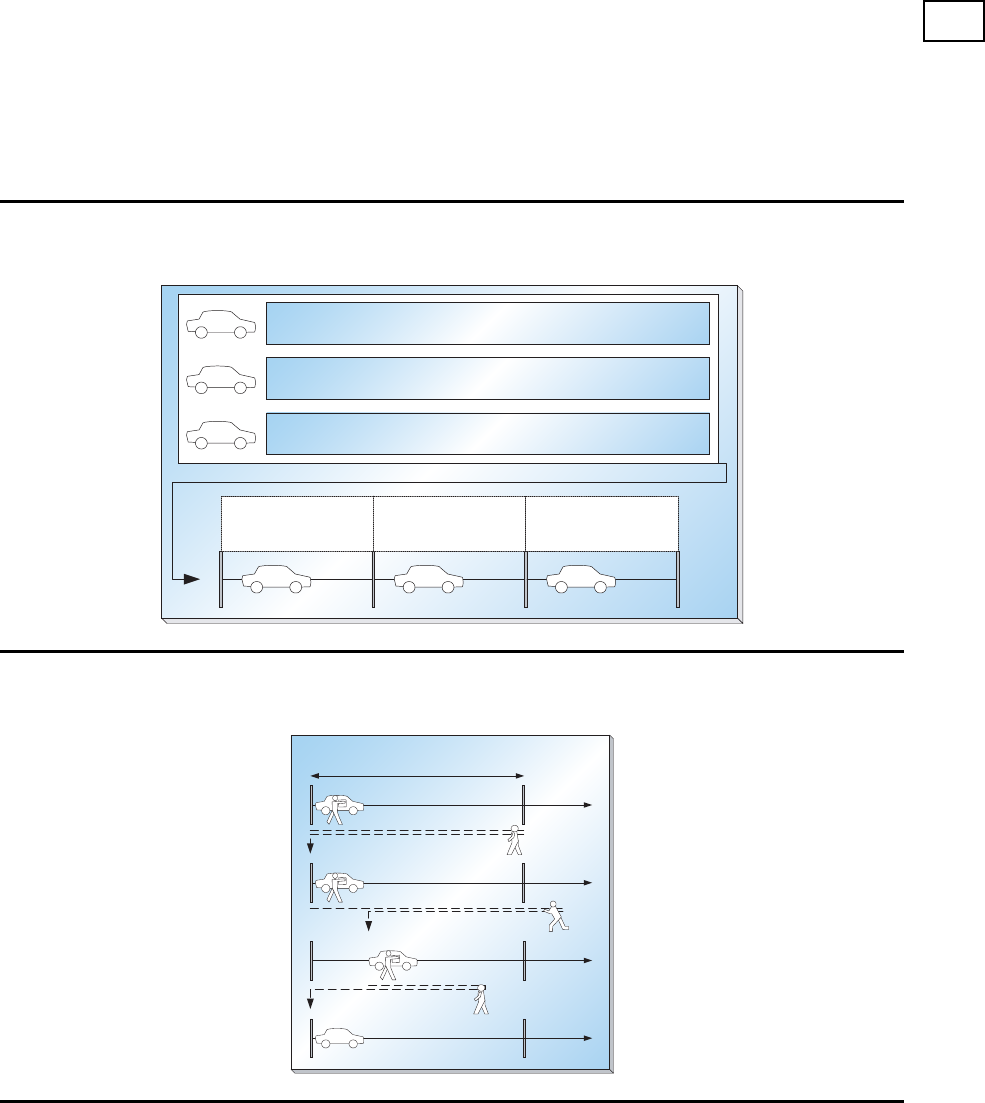
Mehrproduktmontagelinie
ABS+Antenne
2 min + 2 min
Radio
1 min
Schiebedach
3 min
Antenne
2 min
Radio + Fensterheber
1 min + 3 min
Verkleidung
1 min
Antenne
2 min
Radio + Fensterheber
1 min + 3 min
Schiebedach + Verkleidung
3 min + 1 min
Station 1
ABS Vorbereitung
Antenne Kofferraum
Station 2
Radio
elektr. Fensterheber
Station 3
Schiebedach
Verkleidung 5. Tür
Abschwimm- und Aufholbewegung eines Werkers
Idealfall: Arbeitsbelastung = Taktzeit
Länge des Arbeitsbereichs
Überdurchschnittliche Arbeitsbelastung
Unterdurchschnittliche
Arbeitsbelastung
Annahmen
• M Stationen mit der Stationsl¨ange l
m
• W Werkst ¨ucke, Taktzeit C
263
• Berbeitungszeit b
wm
• Identische Reihenfolgen an allen Stationen
• Springereinsatzzeit soll minimiert werden
Beispiel
w 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 L¨ange
Station 1 1.19 1.19 1.19 .82 1.15 1.19 1.19 .94 1.19 .82 .94 .82 .94 1.19 .94 .94 1.2
Takt 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
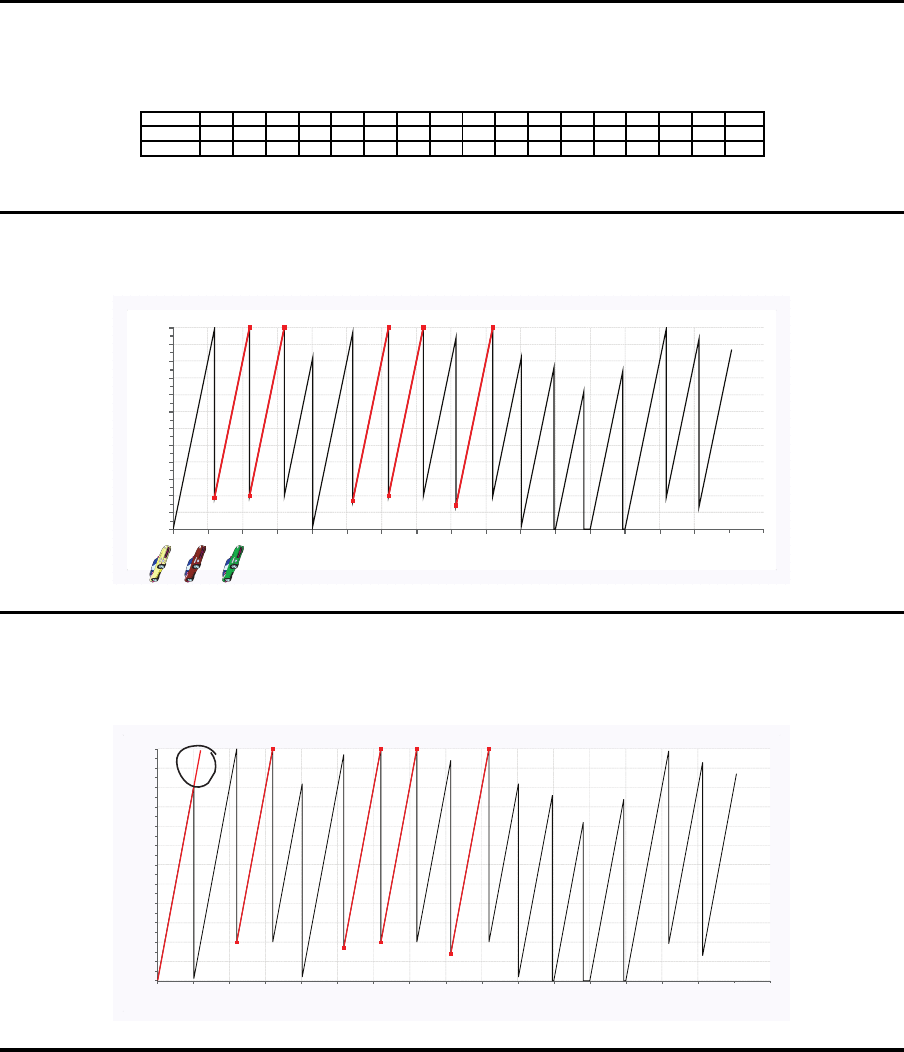
Wege-Zeit-Diagramm
Takt (Werkstück)
1 2345678910 11 12 13 14 15 16
Position des Werkers an Station 1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
1.1
1.2
0.18 0.19 0.16 0.19 0.13
Wege-Zeit-Diagramm
Springereinsatz
Takt (Werkstück)
12345678910 11 12 13 14 15 16
Position des Werkers an Station 1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
1.1
1.2
0.01
0.19 0.16 0.19 0.13
0.19
264
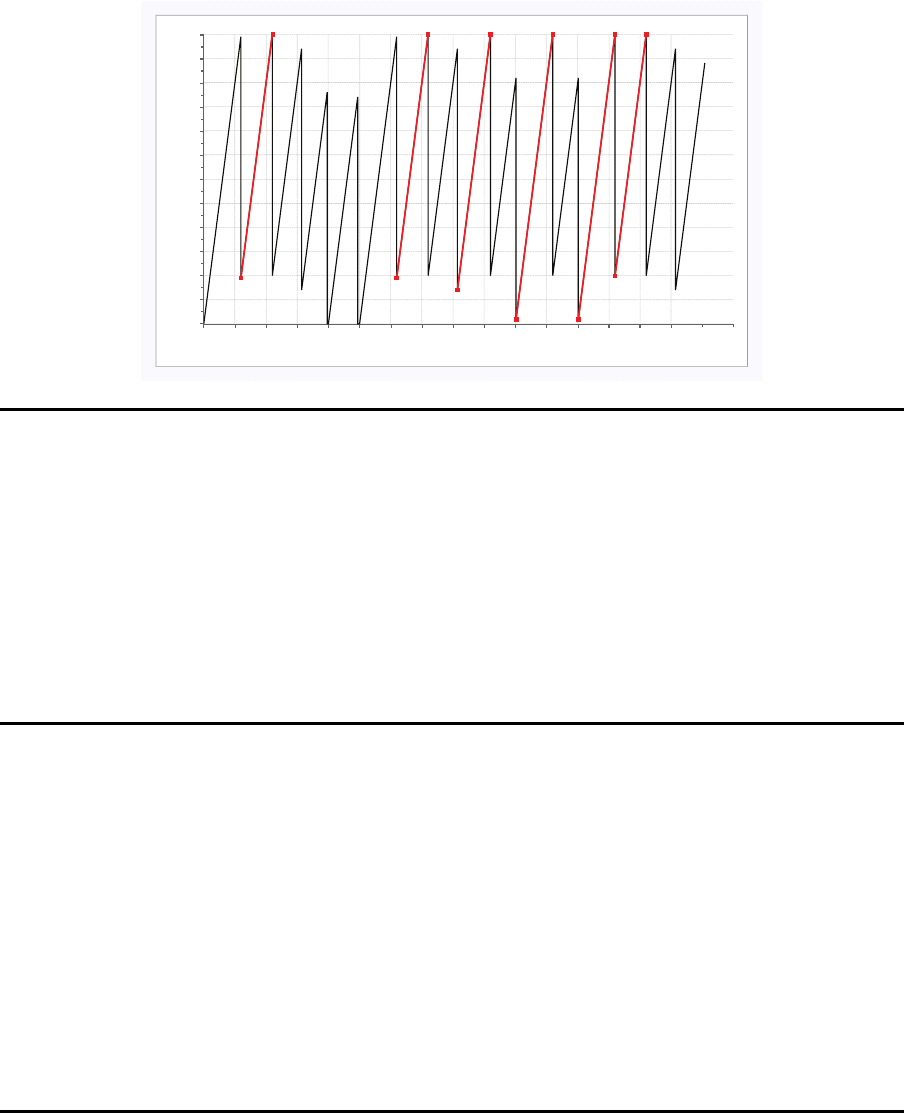
Wege-Zeit-Diagramm
Andere Reihenfolge
Takt (Werkstück)
1513 4116 78910212 3141516
Position des Werkers an Station 1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
1.1
1.2
0.14 0.18 0.13 0.01 0.01 0.19
Optimierungsmodell
Symbole: Daten
W Anzahl der Werkst¨ucke; w = 1, 2, . . . , W
T Anzahl Positionen der Reihenfolge; t = 1, 2, . . . , T
M Anzahl Stationen; m = 1, 2, . . . , M
b
wm
Bearbeitungszeit des Werkst¨ucks w an der Station m
l
m
L¨ange der Station m
C Taktzeit
Optimierungsmodell
Symbole: Variablen
s
mt
Position des Werkers an Station m zu Beginn der Bearbeitung des t-ten
Werkst¨ucks in der Reihenfolge
o
mt
Springereinsatzzeit an Station m f¨ur das t-te Werkst¨uck in der
Reihenfolge
x
wt
=
(
1 wenn das Werks t¨uck w im t-ten Takt eingelastet wird
0 sonst
Modell MMS
Mod e llformulierung
265
Minimiere Z =
M
X
m=1
T
X
t=1
o
mt
u. B. d. R.
T
X
t=1
x
wt
= 1 w = 1, 2, . . . , W
W
X
w=1
x
wt
= 1 t = 1, 2, . . . , T
s
m1
= 0 m = 1, 2, . . . , M
s
mt
+
W
X
w=1
b
wm
· x
wt
−l
m
≤ o
mt
m = 1, 2, . . . , M;
t = 1, 2, . . . , T
s
mt
+
W
X
w=1
b
wm
· x
wt
−C − o
mt
≤ s
m,t+1
m = 1, 2, . . . , M;
t = 1, 2, . . . , T
s
mt
≥ 0, o
mt
≥ 0
m = 1, 2, . . . , M;
t = 1, 2, . . . , T
x
wt
∈ {0, 1}
w = 1, 2, . . . , W ;
t = 1, 2, . . . , T
266
Teil XVI
Instandhaltungspla nung
43 Einf¨uhr ung
Siehe auch Tempelmeier (2018), Teil B, Abschnitt 4
Grundproblem der Instandhaltung
1. Was soll instandgehalten werden?
2. Wie soll die Instandhaltung durchgef¨uhrt werden?
3. Wer f¨uhrt die Instandhaltung durch?
4. Wo soll die Instandhaltung vorgenommen werden?
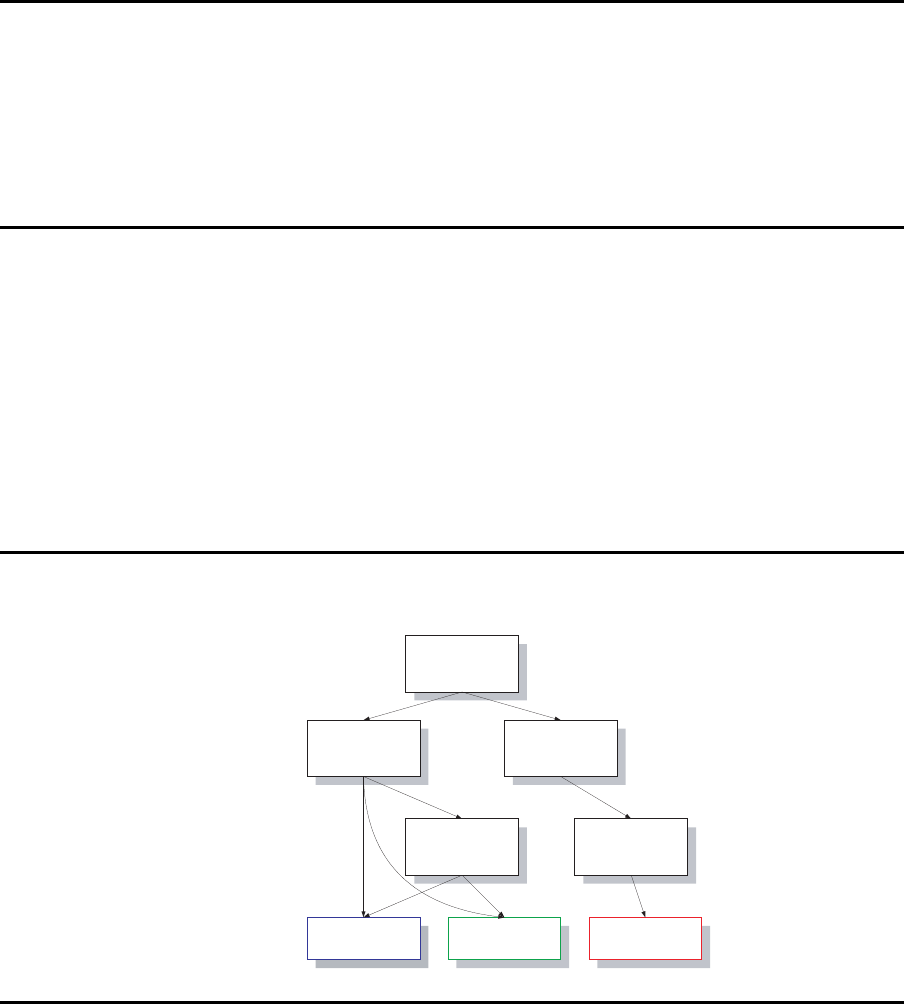
Begriffsabgrenzungen
Instandhaltung
vorbeugend ausfallbedingt
vorbeugende
Reparatur
Ausfallreparatur
Wartung Inspektion Reparatur
Anlaß
Arbeitsinhalt
267
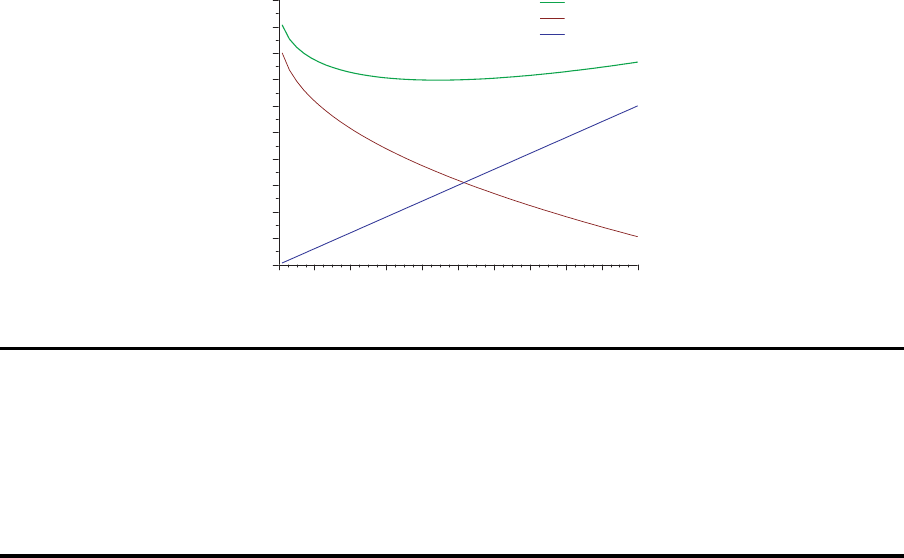
Kostenfunktionen
10
20
30
40
50
60
70
80
90
100
110
Kosten
0 10 20 30 40 50 60 70 80 90 100
Umfang der vorbeugenden Instandhaltung
Gesamt
bei Ausfall
vorbeugend
Problemstellung
• Sollen vorbeugende Instandhaltungsmaßnahmen durchgef¨uhrt werden und wenn ja,
wie hoch ist das optimale Instandhaltungsintervall ?
Daten
• Lebensdauern
• Reparaturzeiten
• Reparaturkosten
• Stillstandkosten
268
44 Instandhaltungsstrategien
44.1 Optimales Instandhaltungsintervall
Ablauf
T
l
T
l
T
l
T
l
T
r
T
r
T
r
T
p
T
l
T
v
T
r
T
p
T
v
T
p
T
v
Fragen
• Wenn vorbeugende Instandhaltung betrieben wird, sind die Einsparungen aufgrund
weniger ungeplanter Ausf¨alle gr¨oßer als die zus¨atzlichen K osten aufgrund der vor-
beugenden R eparaturen, die ja z. T. ¨uberfl¨ussig sein k¨onnen?
• Falls vorbeugende Reparatur sinnvoll ist, wie lang ist das optimale Instandhal-
tungsintervall t
p
?
Ausfallreparaturen
Erwartete Kosten
E {C
r
} = E {B} · c
r
Kosten f¨ur Ausfallreparaturen
c
r
Kosten p ro Ausfallreparatur
E{B} mittlere An zahl von Au sf¨allen pro Period e
E {B} =
N
E {T
l
}
Anzahl Ausf¨alle
Vorbeugende Reparaturen
Erwartete Kosten
E {C
g
(t
p
)} = E {C
r
(t
p
)} + E {C
v
(t
p
)}
269
Vorbeugende Reparaturen
Lebensdauerverteilung
Lebensdauer P {Lebensdauer}
1 0.05
2 0.05
3 0.20
4 0.40
5 0.20
6 0.05
7 0.05
Verfahren
Bestimmung des optimal e n Instandhaltungsintervalls
• Schritt n: Instandhaltungsintervall n
• Berechne die erwartete Anzahl von Ausf¨allen im Zeitraum von n Perioden, E{B
n
}
und bestimme die durchschnittliche Anzahl von Ausf¨allen pro Periode,
E{B
n
}
n
.
• Bestimme die erwarteten Kosten f¨ur Ausfallreparaturen pro Periode,
E{C
r
(n)} = c
r
·
E{B
n
}
n
• Bestimme die erwarteten Ko sten f¨ur vorbeugende Reparaturmaßnahmen pro Peri-
ode,
E{C
v
(n)} = c
v
·
N
n
• Bestimme die gesamten erwarteten Instandhaltungskosten,
E{C
g
(n)} = E{C
r
(n)} + E{C
v
(n)}
f¨ur ein Instandhaltungsintervall der L¨ange n
Berechnung
f¨ur eine Periode
Periode 1
1. Ausfall N · p
1
E {B
1
} = N · p
1
270

Berechnung
f¨ur zwei Perioden
Periode 1 Periode 2
1. Ausfall N · p
1
N · p
2
2. Ausfall ֒→ (N · p
1
) · p
1
=
E{B
1
} · p
1
E {B
2
} = N · (p
1
+ p
2
) + B
1
· p
1
Berechnung
f¨ur drei Perioden
Periode 1 Periode 2 Periode 3
1. Ausfall N · p
1
N · p
2
N · p
3
2. Ausfall ֒→ (N · p
2
) · p
1
֒→ (N · p
1
) · p
2
֒→ (N · p
1
) · p
1
3. Ausfall ֒→ [(N · p
1
) ·
p
1
] · p
1
Zusammenfassung
E {B
3
} =
N · (p
1
+ p
2
+ p
3
)
+ [(N · p
1
) · p
1
+ (N · p
2
) · p
1
+ ((N · p
1
) · p
1
) · p
1
]
+ (N · p
1
) · p
2
= N · (p
1
+ p
2
+ p
3
) + p
1
· [(N · p
1
) + (N · p
2
) + ((N · p
1
) · p
1
)]
+E{B
1
} · p
2
= N · (p
1
+ p
2
+ p
3
) + p
1
· E{B
2
} + p
2
· E{B
1
}
Allgemein
E {B
3
} = N · (p
1
+ p
2
+ p
3
) + p
1
·E {B
2
} + p
2
· E {B
1
}
E {B
n
} = N ·
n
X
i=1
p
i
+ p
1
· E { B
n−1
} + p
2
· E { B
n−2
} + . . . +
271

+ p
n−1
· E { B
1
}
Beispiel, n=1
N = 60 Maschinen; c
r
= 300; c
v
= 100.
E{B
1
} = N · p
1
= 60 · 0.0 5 = 3
E{C
r
(1)} = c
r
·
E{B
1
}
1
= 300 ·
3
1
= 900
E{C
v
(1)} = c
v
· 60/1 = 100 ·
60
1
= 6000
E{C
g
(1)} = 6900
Beispiel, n=2
E{B
2
} = E{B
1
} · p
1
+ N · (p
1
+ p
2
)
= 3 · 0.05 + 60 · (0.05 + 0.05) = 6.15
E{C
r
(2)} = c
r
·
E{B
2
}
2
= 300 ·
6.15
2
= 922.50
E{C
v
(2)} = c
v
·
60
2
= 100 ·
60
2
= 3000
E{C
g
(2)} = 3922.50
272
Beispiel, n=3
E{B
3
} = N · (p
1
+ p
2
+ p
3
) + p
1
· E{B
2
} + p
2
·E{B
1
}
= 60 · (0.30) + 0.05 · 6.15 + 0.05 · 3
= 18.4575
E{C
r
(3)} = c
r
·
E{B
3
}
3
= 300 ·
18.4575
3
= 300 · 6 .1525
= 1845.75
E{C
v
(3)} = c
v
·
60
3
= 100 ·
60
3
= 2000
E{C
g
(3)} = 3845.75
Kosten
f¨ur Ausfallreparaturen
E{C
r
} = c
r
·
N
E{T
b
}
= 300 ·
60
4
= 4500
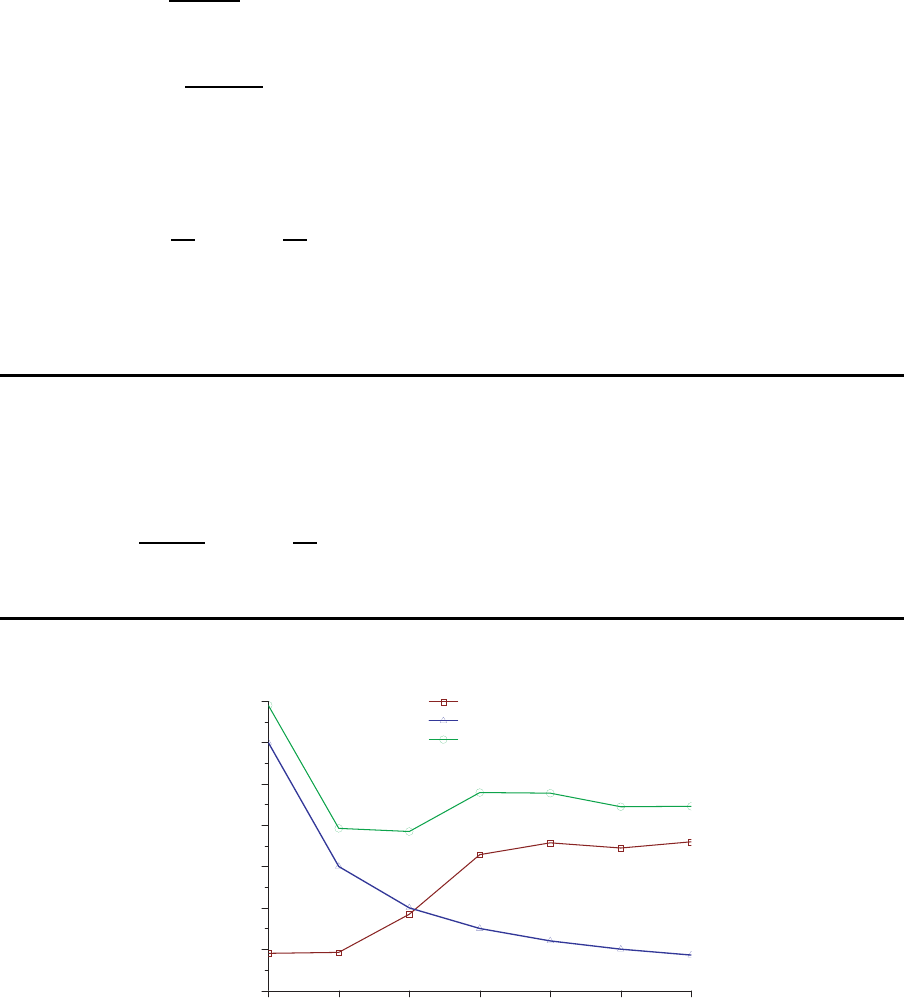
Kosten
0
1000
2000
3000
4000
5000
6000
7000
Kosten
1 2 3 4 5 6 7
Instandhaltungsintervall
Kosten der Ausfallreparaturen
Kosten der vorbeugenden Reparaturen
Gesamtkosten
273