
2
5 Standortp lanung mit bekannten potentiellen Stan-
dorten
Annahmen
• gegebene Menge von potentiellen Standorten
• gegebene Entfernungen in einem Straßennetz
• Transportkosten pro Mengeneinheit konstant
5.1 Standardmodell: Simple Plant Location Model
Modell STAND ORT
Symbole
b
i
Produk tionskapazit¨at des Standorts i
c
ij
Transportkosten zwischen Standort i und Abnehmerzentrum j (pro
Mengeneinheit)
d
j
Bedarfsmenge des Abnehm er zentrums j
f
i
Fixkosten pro Jahr am Standort i
I Anzahl der potentiellen Standorte (i = 1, 2, ..., I)
J Anzahl der Abnehmerzentren (j = 1, 2, ..., J)
Modell STAND ORT (SPLP, Simple Plant Location Problem)
Minimiere Z =
I
X
i=1
f
i
· γ
i
+
I
X
i=1
J
X
j=1
c
ij
· x
ij
u. B. d. R.
I
X
i=1
x
ij
= d
j
j = 1, 2, ..., J
J
X
j=1
x
ij
≤ b
i
· γ
i
i = 1, 2, ..., I
x
ij
≥ 0 i = 1, 2, ..., I; j = 1, 2, ..., J
10

Modell STAND ORT
γ
i
∈ {0, 1} i = 1, 2, ..., I
Disaggregierte Formulierung (Valid inequalities)
x
ij
≤ d
j
· γ
i
i = 1, 2, ..., I; j = 1, 2, ..., J
Diese Neb enbedingungen werden zum Modell STANDORT hinzugef¨ugt.
5.2 Erl¨auterungen zur disaggregierten Formulierung
Das Modell STANDORT (SPLP, Simple Plant Location Problem) ist ein gemischt-ganz-
zahliges Optimierungsproblem. Zu seiner L¨osung kann man ein Branch-and-Bound-
Verfahren einsetzen. Dabei ersetzt man die Restriktionen γ
i
∈ {0, 1} durch 0 ≤ γ
i
≤ 1 f¨ur
alle oder einige der γ-Variablen. Man relaxiert das Modell. Ein so entstandenes (partiell)
relaxiertes Modell ist ein kontinuierliches LP-Modell, das mit dem Simplex-Verfahren op-
timal gel¨ost werden kann. Die optimale L¨osung enth¨alt normalerweise nicht-ganzahlige
(und damit auch f¨ur da s urspr¨ungliche Modell nicht-zul¨assige, d. h. nicht-bin¨are) Werte
der γ-Variablen. Der Zielwert der optimalen L¨osung des relaxierten Modells bildet
eine unter e Schranke (lower bound, LB) des optimalen Zielwertes f¨ur das Modell mit
zul¨assigen (bin¨aren) Werten der γ-Variablen.
Sind alle γ-Variablen in der optimalen L¨osung eines relaxierten LP-Modells ganzzahlig,
dann hat man eine zul¨assige L¨osung gefunden. Ihr Zielwert bildet eine obere Schranke
(upper bound, UB) f¨ur den optimalen Zielwert des Modells STANDORT. Die Differenz
dieser beiden Schranken gibt die maximale Abweichung einer gefundenen L¨osung vom
exakten Optimum an, das zwischen diesen beiden Schranken liegt.
Im Rahmen des Branch&Bound-Verfahrens verzweigt man ¨uber eine ausgew¨ahlte γ-
Variable und zerteilt den L¨osungsraum dabei in zwei disjunkte Teilmengen, f¨ur die j eweils
ein (partiell, d. h. nur bez¨uglich einiger Bin¨ar variablen) relaxiertes LP-Modell entsteht.
Nach der L¨osung eines (par t iell) relaxierten Problems kann der Verzweigungsprozeß an
dem betreffenden Ast des L¨osungsbaums abgebrochen werden,
1. wenn das relaxierte Problem keine zul¨assige L¨osung hat
2. wenn alle ganzzahligen Variablen auch tats¨achlich ganzzahlige Werte annehmen
(dann hat man m¨oglicherweise eine bessere obere Schranke gefunden)
3. wenn der optimale Zielwert des aktuellen (relaxierten) Problems schlechter
ist als der Zielwert der besten bekannte g anzzahligen L¨osung (obere Schranke). In
diesem Fall f¨uhren weitere Verzweigungen nur noch zu L¨osungen, die nicht besser
sein k¨onnen als die beste bisher bekannte zul¨assige L¨osung.
Das folgende Bild zeigt einen Teil des L¨osungsbaums f¨ur ein Problem mit drei potentiellen
Standorten.
11
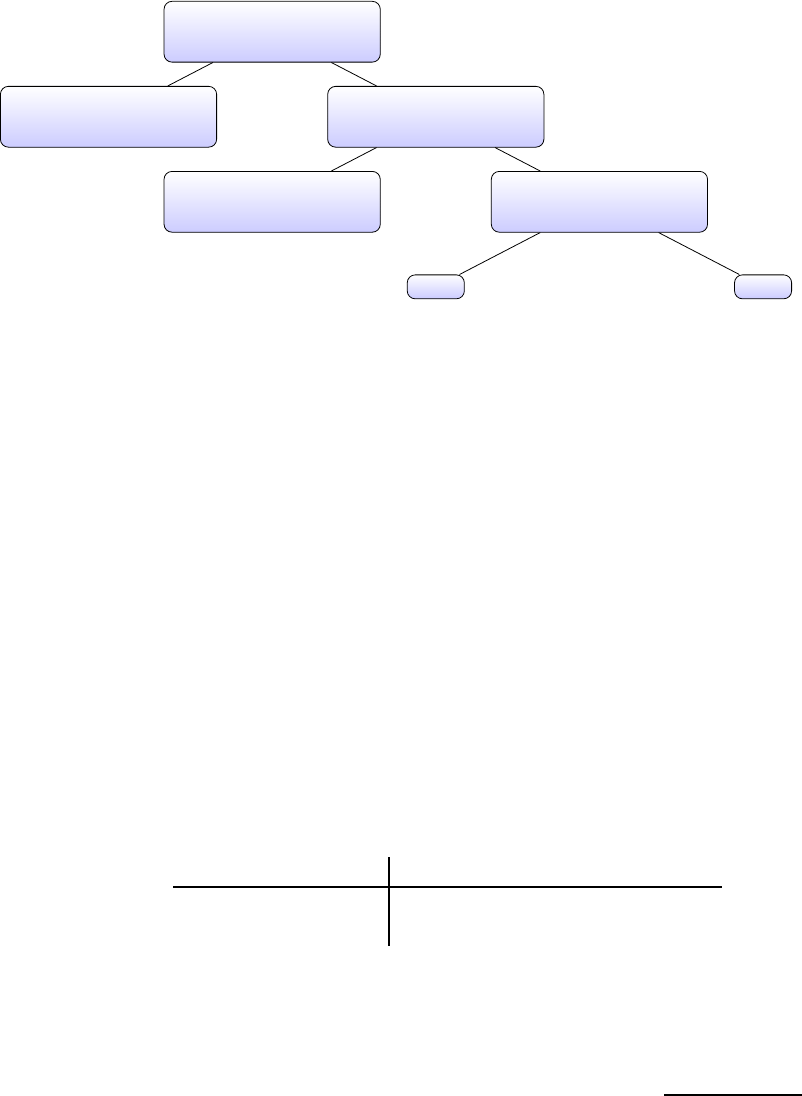
Branch-and-Bound
LP
0
:
γ
1
≥ 0, γ
2
≥ 0, γ
3
≥ 0
LP
1
:
γ
1
= 0, γ
2
≥ 0, γ
3
≥ 0
LP
2
:
γ
1
= 1, γ
2
≥ 0, γ
3
≥ 0
LP
5
:
γ
1
= 1, γ
2
= 0 , γ
3
≥ 0
LP
6
:
γ
1
= 1, γ
2
= 1 , γ
3
≥ 0
usw. usw.
Je h¨oher der Zielwert eines relaxierten Modells ist, umso eher kann die weitere Verzwei-
gung in dem betreffenden Ast des L¨osungsbaums abgebrochen werden. Die disag-
gregierte Formulierung (mit valid inequalities, cutting planes, Schnittebenen) soll
dazu f¨uhren, daß die Zielwert e der par tiell relaxierten LP-Modelle m¨oglichst hoch sind.
Betrachten wir einmal die Nebenbedingungen
J
X
j=1
x
ij
≤ b
i
· γ
i
(1)
F¨ur das urspr¨ungliche Modell mit bin¨aren γ-Var iablen erf¨ullen diese Bedingungen ihren
Zweck, n¨amlich sicherzustellen, daß nur vo n einem gew¨ahlten Standort Transpo r tstr¨ome
ausgehen.
L¨ost man f¨ur das Beispiel aus Abschnitt 5.4 das relaxierte Modell, da nn werden die
γ-Variablen sehr klein, wenn f¨ur einen Standort i nur ein kleiner Teil der Kapazit¨at
genutzt wird. Im Beispiel erh¨alt man z. B. die optimalen Werte γ
1
= 0.48, γ
2
= 0.54286,
γ
3
= 0.14286 und γ
4
= 0.44 mit dem Zielwert 167265.71. Die optimale zul¨assige L¨osung
hat ¨ubrigens den Zielwert 222 280.
Variable γ
1
γ
2
γ
3
γ
4
Optimale L¨osung 0 1 1 0
Relaxiertes Modell 0.48 0.54286 0.14286 0.44
Table 1: L¨osungen des Beispiels
In der relaxierten L¨osung sind alle vier Standorte (wenigstens zum Teil) ge¨offnet, w¨ahrend
die optimale L¨osung nur zwei Standorte enth¨alt. Die relative Differenz zwischen der
unteren Schranke des Zielwertes und dem optimalen Zielwert ist
222280−167265.71
222280
= 24.7%.
Die aggregierte Nebenbedingung (1) stellt sicher, daß die gesamte Transportmenge,
die den Standort i verl¨aßt, nicht gr¨oßer ist als die Kapazit¨at b
i
dieses Standortes. Man
kann aber noch eine strengere Beziehung zwischen den Transpo r tmengen und den γ-
Variablen formulieren: Fall s der Standort i genutzt wird, dann kann die Transportmenge
von diesem Standort zum Abnehmer j nicht gr¨oßer sein als die Nachfragemenge dieses
Abnehmers.
12

Also kann man zus¨atzlich zu (1) noch verla ngen:
x
ij
≤ d
j
· γ
i
i = 1, 2, . . . , I; j = 1, 2, . . . , J (2)
Diese Bedingungen sind in der optimalen L¨osung des urspr¨unglichen Modells (mit ganz-
zahligen Werten der γ-Variablen) immer erf¨ullt. In einem relaxierten Modell muß das
aber nicht sein. Dies f¨uhrt dazu, daß L¨o sungen des relaxi erten Modells, die im Hinblick
auf (1) zul¨assig sind, nun im Hinbl i c k auf (2) unzul¨assig sind und damit aus der L¨osung
ausgeschlo ssen werden.
Betrachten wir die LP-Relaxation des aggregierten Modells aus der obigen Tabelle. F¨ur
Standort i = 1 ist γ
1
= 0.48 und aus der Kapazit¨atsrestriktion ergibt sich
J
X
j=1
x
ij
≤ b
i
· γ
i
→ 0 + 0 + 0 + 120
|{z}
x
14
+0 ≤ 250
|{z}
b
1
·0.48
Setzt man diesen Wert in (2) ein, dann ergibt sich f¨ur j = 4:
x
14
≤ d
4
· γ
1
→ 120 ≤ 0.48 · 120 → 120 57.6
F¨uhrt man also die Bedingungen
x
1j
≤ d
j
· γ
1
j = 1, 2, 3, 4 , 5
zus¨atzlich in das relaxierte LP-Modell ein, dann ist γ
1
= 0.48 keine zul¨ass i ge L¨osung des
relaxierten Modells. St attdessen erh¨alt man
Variable γ
1
γ
2
γ
3
γ
4
L¨osung 0 0.54286 0.48571 0.44
Table 2: Relaxiertes Modell (1)
F¨ur Standort i = 2 ist γ
2
= 0.54286 und a us der Ka pazit¨atsrestriktion ergibt sich
J
X
j=1
x
ij
≤ b
i
· γ
i
→ 100
|{z}
x
21
+ 90
|{z}
x
22
+0 + 0 + 0 ≤ 350 ·0.54286
Jetzt werden j = 1 und j = 2 beliefert. Wir pr¨ufen die L¨osung bez¨uglich der Nebenbe-
dingungen (2).
j = 1 : x
21
≤ d
1
·γ
2
→ 100 ≤ 100 · 0.54286 → 100 54.286
j = 2 : x
22
≤ d
2
·γ
2
→ 90 ≤ 90 · 0.5 4286 → 90 48.86
Die L¨osung ist also bez¨uglich (2) unzul¨assig. Um diese L¨osungen auszuschließen, f¨uhren
wir nun zus¨atzlich die Bedingungen
x
2j
≤ d
j
· γ
2
j = 1, 2, 3, 4 , 5
13
in das relaxierte LP-Modell ein und erhalten
Variable γ
1
γ
2
γ
3
γ
4
L¨osung 0 1 0.14286 0.44
Table 3: Relaxiertes Modell (2)
Die Transportmengen vom Standort 2 aus (m
21
= 100, m
22
= 90 und m
24
= 120) erf¨ullen
nun alle Restriktionen. F¨ur Standort 3 ergibt sich m
35
= 50.
x
35
≤ d
5
· γ
3
→ 50 ≤ 50 · 0.14286 → 50 7.143
Wir f¨uhren nun die Bedingungen
x
3j
≤ d
j
· γ
3
j = 1, 2, 3, 4 , 5
zus¨atzlich in das relaxierte LP-Modell ein und erhalten
Variable γ
1
γ
2
γ
3
γ
4
L¨osung 0.097436 0.95897 0 0.4 4
Table 4: Relaxiertes Modell (3)
Die Transportmengen sind jetzt
j 1 2 3 4 5
x
1j
4.102564103 3.692307692 0 11.6923076 9 4.871794872
x
2j
95.8974359 86.30769231 0 108.3076923 45.12820513
x
3j
0 0 0 0 0
x
4j
0 0 110 0 0
d
j
100 90 110 120 50
Table 5: Relaxiertes Modell (3) Transportmengen
Die Mengen von den Stando r ten 1 bis 3 erf¨ullen alle Restriktionen. F¨ur Standort 4 werden
die Nebenbedingungen (2) nicht erf¨ullt, da 110 110 ·0.44. Deshalb f¨uhren wir jetzt die
letzte Gruppen von Restriktionen
x
4j
≤ d
j
· γ
4
j = 1, 2, 3, 4 , 5
in das relaxierte LP-Modell zus¨atzlich ein und erhalten eine bez¨uglich (1) und (2) zul¨assige
L¨osung, die obendrein auch noch optimal ist.
Eine solche Nebenbedingung, die auch f¨ur alle (ganzzahligen) zul¨assigen L¨osungen eines
ganzzahligen Optimierungsmodells erf¨ullt ist, nennt man valid inequality. Damit sie
die LP-Relaxation verbessert, muß sie L¨osungen aus dem relaxierten Modell entfernen,
die bez¨uglich des urspr¨unglichen ganzzahligen Modells unzul¨assig sind.
Durch die schrittweise Einf¨uhrung der Restriktionen (2) ergeben sich folgende Zielwerte
14

Schritt 0 1 2 3 4
LB 167265.71 186688 .57 193722.86 202924.103 222280
Table 6: Entwicklung der unteren Schranke
F¨ur das betrachtete Beispiel erh¨alt man bereits mit dem vollst¨andig relaxierten Modell
und den Bedingungen (2 ) die optimale ganzzahlige L ¨osung. Ein weiteres Verzweigen im
Branch&Bound-Verfahren ist daher hier nicht mehr n¨otig.
Das ist aber nicht immer so. Betrachten wir das folgende OPL-Modell f¨ur ein Beispiel
mit 8 potentiellen Standorten und 14 Abnehmerzentren.
// Daten:
Abnehmer = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14;
Standort = 1, 2, 3, 4, 5, 6, 7, 8;
d = [ 250 150 1000 80 50 800 325 100 475 220 900 1500 430 200]; //
Nachfrage
b = [ 5000 5000 5000 5000 5000 5000 5000 5000]; // Kapazit¨at
f = [ 2400 7000 3600 1600 3000 4600 9000 2000]; // Fixkosten
c = [
[ 1.25 0.80 0.70 0.90 0.80 1.10 1.40 1.30 1.50 1.35 2.10 1.80 1.60 2.00 ]
[ 1.40 0.90 0.40 1.20 0.70 1.70 1.40 1.50 1.90 1.60 2.90 0.26 2.00 2.40 ]
[ 1.10 0.90 0.80 1.40 0.60 1.10 1.25 1.00 1.70 1.30 2.40 2.20 1.90 2.00 ]
[ 0.90 1.30 1.70 0.50 0.70 0.60 0.80 1.10 1.30 1.30 1.90 1.80 1.90 2.20 ]
[ 1.50 1.40 1.60 1.55 1.45 0.90 0.80 0.70 0.40 1.00 1.10 0.95 1.40 1.50 ]
[ 1.90 2.20 2.50 1.70 1.80 1.30 1.00 1.50 0.80 1.20 2.00 0.50 1.00 1.20 ]
[ 2.00 2.10 2.05 1.80 1.70 1.30 1.00 1.50 0.70 1.10 0.80 2.00 0.90 1.10 ]
[ 2.10 1.80 1.60 1.40 1.30 1.40 1.10 1.00 0.80 0.70 1.20 1.00 0.80 0.80 ]
];
// Modell:
// SPLP
int Abnehmer = ...;
int Standort = ...;
int b[Standort] = ...; // Kapazit¨at
int d[Abnehmer] = ...; // Nachfrage
int f[Standort] = ...; // Fixkosten
float c[Standort,Abnehmer] =...; // Transportkosten
dvar float+ m[Standort,Abnehmer];
dvar float+ gamma[Standort] in 0..1; // relaxiert
minimize sum(i in Standort, j in Abnehmer) c[i,j] * m[i,j] +
sum(i in Standort)f[i]* gamma[i];
subject to{
forall(i in Standort)
sum(j in Abnehmer) m[i,j] <= b[i] * gamma[i];
forall (j in Abnehmer)
sum(i in Standort) m[i,j] == d[j] ;
}
Mit der vollst¨andig relaxierten Variante des Modells STANDORT erh¨alt man folgende
L¨osung:
Variable γ
1
γ
2
γ
3
γ
4
γ
5
γ
6
γ
7
γ
8
Relaxiertes Modell 0.23 0 0 0.301 0.115 0 0 0.65
15

Der Zielwert betr¨agt 8036.6. Dieser Wert ist eine unter e Schranke f¨ur den optimalen
Zielwert des urspr¨unglichen Modells. Die optimale zul¨assige L¨osung hat einen Zielwert
von 10153. Daraus ergibt sich eine relative Differenz zwischen der optimalen L¨osung und
der unteren Schranke von
8036.6−10153
10153
= 20.84%.
Wir erg¨anzen das obige OPL-Modell nun um folgende Nebenbedigungen:
forall (i in Standort, j in Abnehmer)
m[i,j] <= d[j] * gamma[i];
Der optimale Zielwert dieses immer noch relaxierten Modells betr¨agt 10033.685. Die
relative Differenz zwischen dem optimalen Zielwert des urspr¨unglichen Modells und dieser
unteren Schranke betr¨agt aber nur noch 1.1 7%.
Variable γ
1
γ
2
γ
3
γ
4
γ
5
γ
6
γ
7
γ
8
Relaxiertes Modell ohne (2) 0.23 0 0 0.301 0.115 0 0 0.65
Relaxiertes Modell mit (2) 0 0 0 0.53 72 0 0 0 1
Je h¨oher die untere Schra nke, umso schneller wird im jetzt noch durchzuf¨uhrenden
Branch&Bound-Verfahren die optimale L¨osung gefunden.
16

5.3 Verlauf der Zielfunktion
Literaturhinweis
Tempelmeier (2018), Aufgabe A1.3
AMPL-Modell; L¨osung mit CPLEX; Branch&Bound-Verfahren
set ORIG; # potentielle Standorte
set DEST; # Abnehmerzentren
param supply {ORIG} >= 0; # Kapazit¨aten
param demand {DEST} >= 0; # Bedarfsmengen
param vcost {ORIG,DEST} >= 0; # variable
Transportkosten
var Trans {ORIG,DEST} >= 0; # Transportmengen
param fcost {ORIG} >= 0; # Fixkosten
var Gamma {ORIG} binary; # = 1 Bin¨arvariable
# Zielfunktion
minimize total cost:
sum {i in ORIG, j in DEST} vcost[i,j] * Trans[i,j]
+ sum {i in ORIG} fcost[i] * Gamma[i];
AMPL-Modell; L¨osung mit CPLEX; Branch&Bound-Verfahren
# Angebotsrestriktionen
subject to Supply {i in ORIG}: sum {j in DEST}
Trans[i,j] <= supply[i] * Gamma[i];
# Nachfragerestriktionen
subject to Demand {j in DEST}: sum {i in ORIG}
Trans[i,j] = demand[j];
# Festlegung der gew¨unschten Anzahl Standorte
subject to Anzahl: sum {i in ORIG} Gamma[i]= 1;
AMPL
Daten
set ORIG := DO HB KA PA WU N;
set DEST := HH B M K F KS;
param supply := DO 900 HB 900 KA 900 PA 900 WU 900 N
900;
param demand := HH 100 B 90 M 110 K 120 F 50 KS 40;
param fcost := DO 20000 HB 20000 KA 20000 PA 20000 WU
20000 N 20000;
param vcost : HH B M K F KS:=
DO 342 500 612 94 219 165
HB 119 390 745 324 467 281
KA 631 687 277 313 145 323
PA 827 639 195 630 443 489
WU 526 470 273 325 116 223
N 607 431 162 432 223 304;
17