4
40.2
¨
Ubertragung des R¨ustzustands im CLSP-L
Das Modell CLSP basiert auf der Annahme, daß ein neuer R¨ustvorgang notwendig ist,
sobald in einer Periode produziert wird. Dabei wird der Fall vernachl¨assigt, daß die
Produktion am Ende einer Periode unterbrochen und am Beginn der n¨achsten Peri-
ode ohne einen R¨ustvorgang fortgesetzt werden kann. Diese Situation tritt u. a. a uch
dann auf, wenn man sehr kurze Planungsperio den verwendet. In diesem Fall muß die
¨
Ubertragung des R¨ustzustands zwischen aufeinanderfolgenden Perioden im Modell er-
faßt werden. Das folgende Bild zeigt einen Produktionsplan, bei dem der R¨ustzustand
der Ressource ber¨ucksichtigt wird.
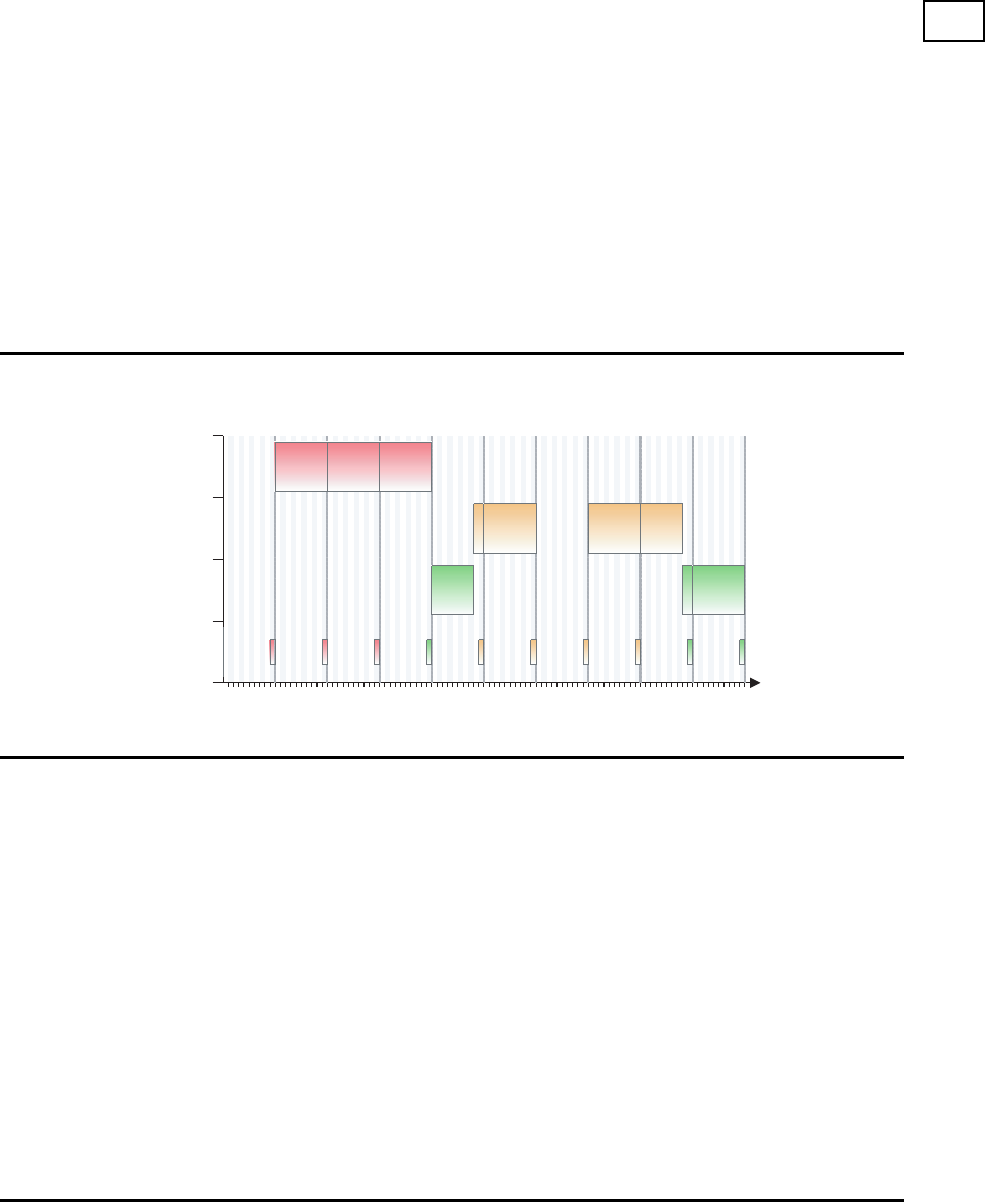
Ein typischer Produktionsplan
50 100 150 200 250 300 350 400 450 500
Zeit
P-1
P-2
P-3
Rüst
Produkt
50 50 50
10 50 50 40
40 10 50
1 1 1 3 2 2 2 2 3 3
¨
Ubertragung des R¨ustzustands
a) ein Produkt wird als letztes in Periode t − 1 und als erstes in Periode t produziert
b) a m Ende der Periode t −1 wird Leerzeit der Maschine genutzt, um f¨ur das erste in
Periode t zu produzierende Produkt umzur¨usten
Falls in der Periode t − 1 ¨uberhaupt nicht produziert wird,
c) kann ger¨ustet und der R¨ustzustand in die n¨achste Periode ¨ubertragen werden
d) kann der aus der Vorperiode ¨ubernommene R¨ustzustand in die n¨achste Periode
¨ubertragen werden
250
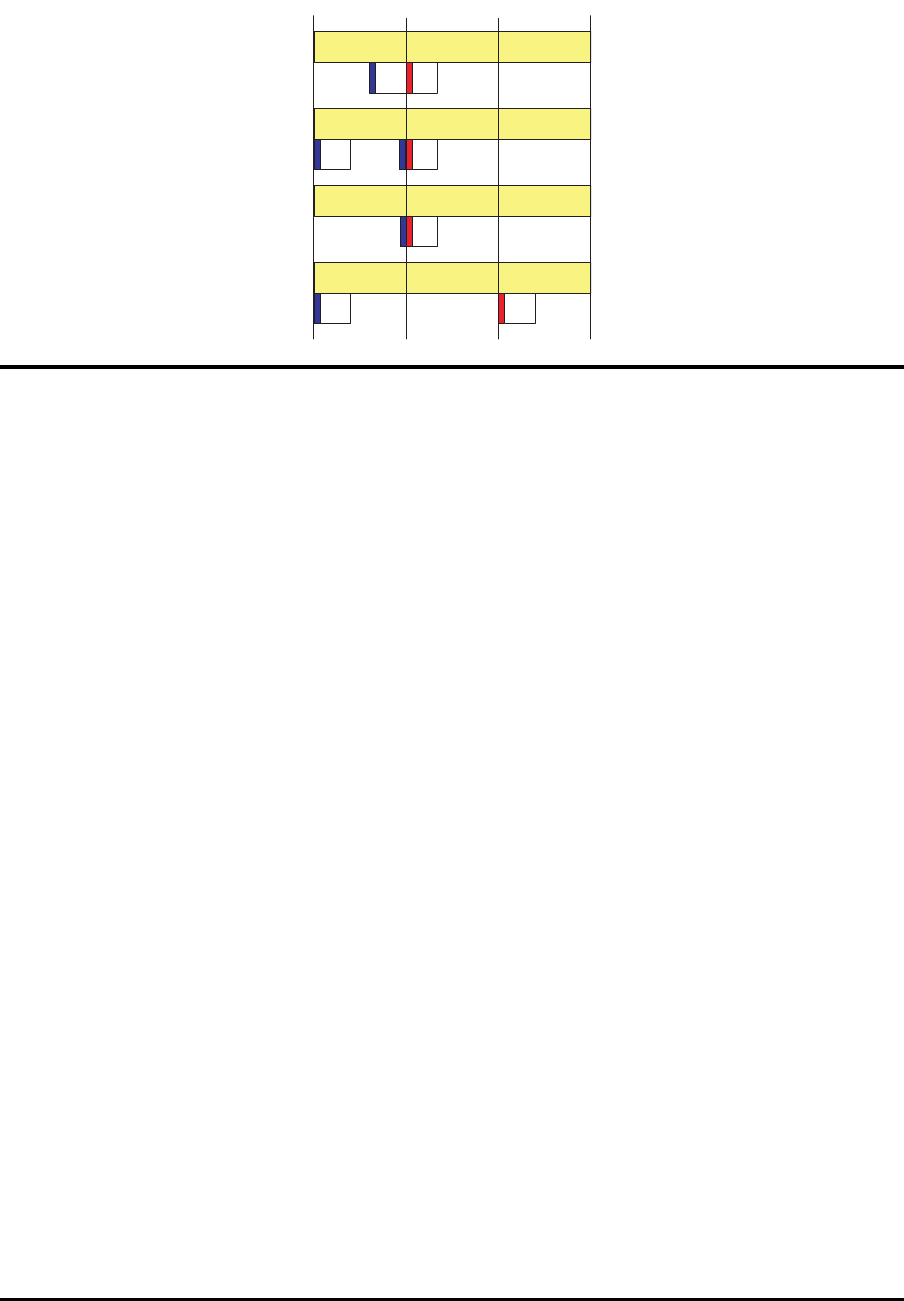
¨
Ubernahme des R¨ustzustands
100 80
20
80
50
80 80
Fall A
Fall B
Fall C
Fall D
1 2 3
Modell CLSP-L
Minimiere Z =
K
X
k=1
T
X
t=1
s
k
· γ
kt
+
K
X
k=1
T
X
t=1
T
X
τ =t
h
ktτ
· δ
ktτ
u. B. d. R.
τ
X
t=1
δ
ktτ
= 1 k = 1, 2, ..., K; τ = 1, 2, ..., T
δ
ktτ
≤ γ
kt
+ ω
kt
k = 1, 2, ..., K; t = 1, 2, ..., T;
τ = t, t + 1, ..., T ; d
τ
> 0
K
X
k=1
"
T
X
τ =t
tb
k
· d
kτ
· δ
ktτ
+ tr
k
· γ
kt
#
≤ b
t
t = 1, 2, ..., T
K
X
k=1
ω
kt
≤ 1 t = 1, 2, ..., T
ω
kt
≤ γ
k,t−1
+ ω
k,t−1
k = 1, 2, ..., K; t = 2, ..., T
Neue Hilfsvariable: v
t
ω
kt
+ ω
k,t+1
≤ 1 + v
t
k = 1, 2, ..., K; t = 1, 2, ..., T − 1
v
t
+ γ
kt
≤ 1 k = 1, 2, ..., K; t = 1, 2, ..., T
251
Modell CLSPL II
Daten d es Beispiel s
Bedarfsmengen Kosten und Zeiten
Periode t
Produkt k 1 2 3 4 5 6 h
k
s
k
tb
k
tr
k
1 30 – 80 – 40 – 4 400 1 10
2 – – 30 – 70 – 3 150 1 10
3 – – 40 – 60 – 2 100 1 10
4 – – 20 – – 10 2 100 1 10
5 – – 60 – 50 – 1 100 1 10
Modell CLSPL III
Optimale L¨osung de s Beispiels aus Tempelm eier (2017 )
Periode t
Produkt k 1 2 3 4 5 6
1 ✕❒ ❒ ❒ – – –
2 – – ✕❒ ➠ ❒ –
3 – – ✕❒ – ✕❒ –
4 ✕❒ – – – – ✕❒
5 ✕❒ – – – ✕❒ –
1 30 10 110 – – –
2 – – 30 – 70 –
3 – – 40 – 60 –
4 20 – – – – 10
5 60 – – – 50 –
Belastung 140 10 200 – 200 20
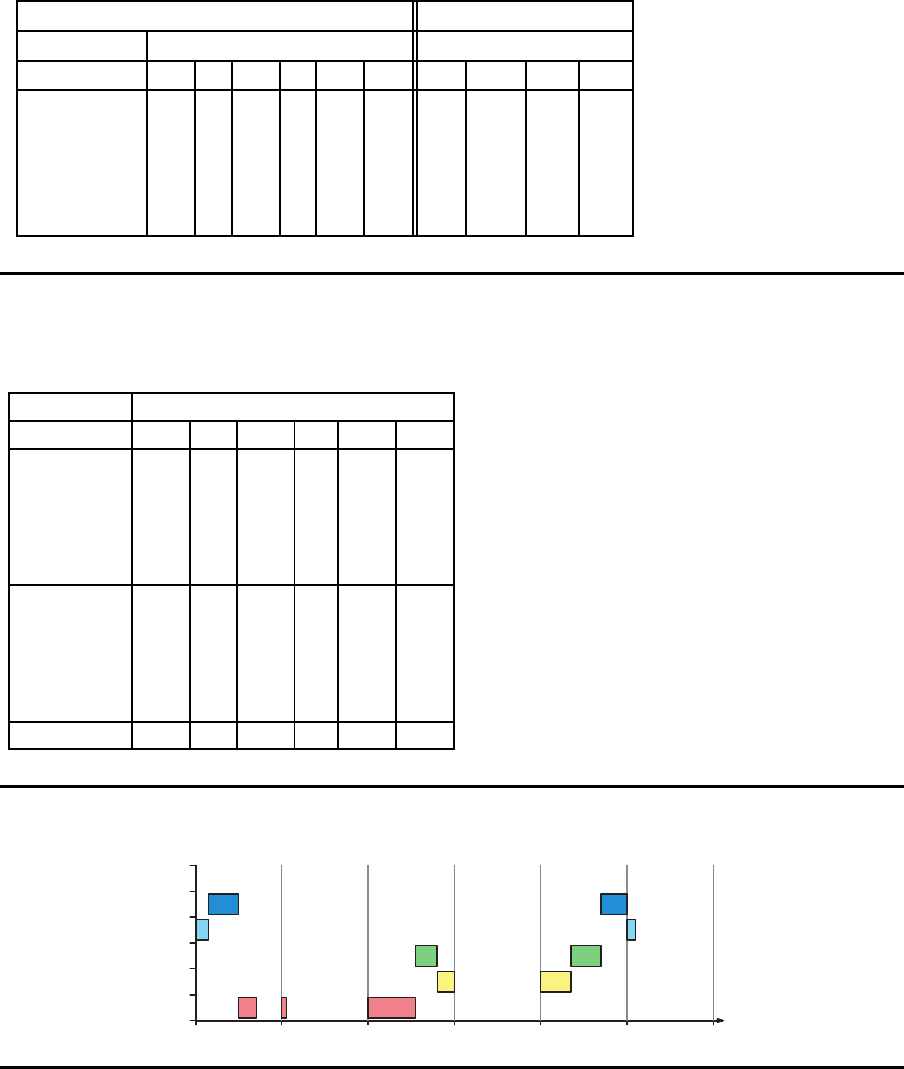
Modell CLSPL V
0 200 400 600 800 1000
120
P1
P2
P3
P4
P5
Z
10+30
0+10 0+110
10+30 0+70
10+40
10+60
10+20
10+10
10+60 10+50
1 1 2 2
0
CLSP-L¨osung
252
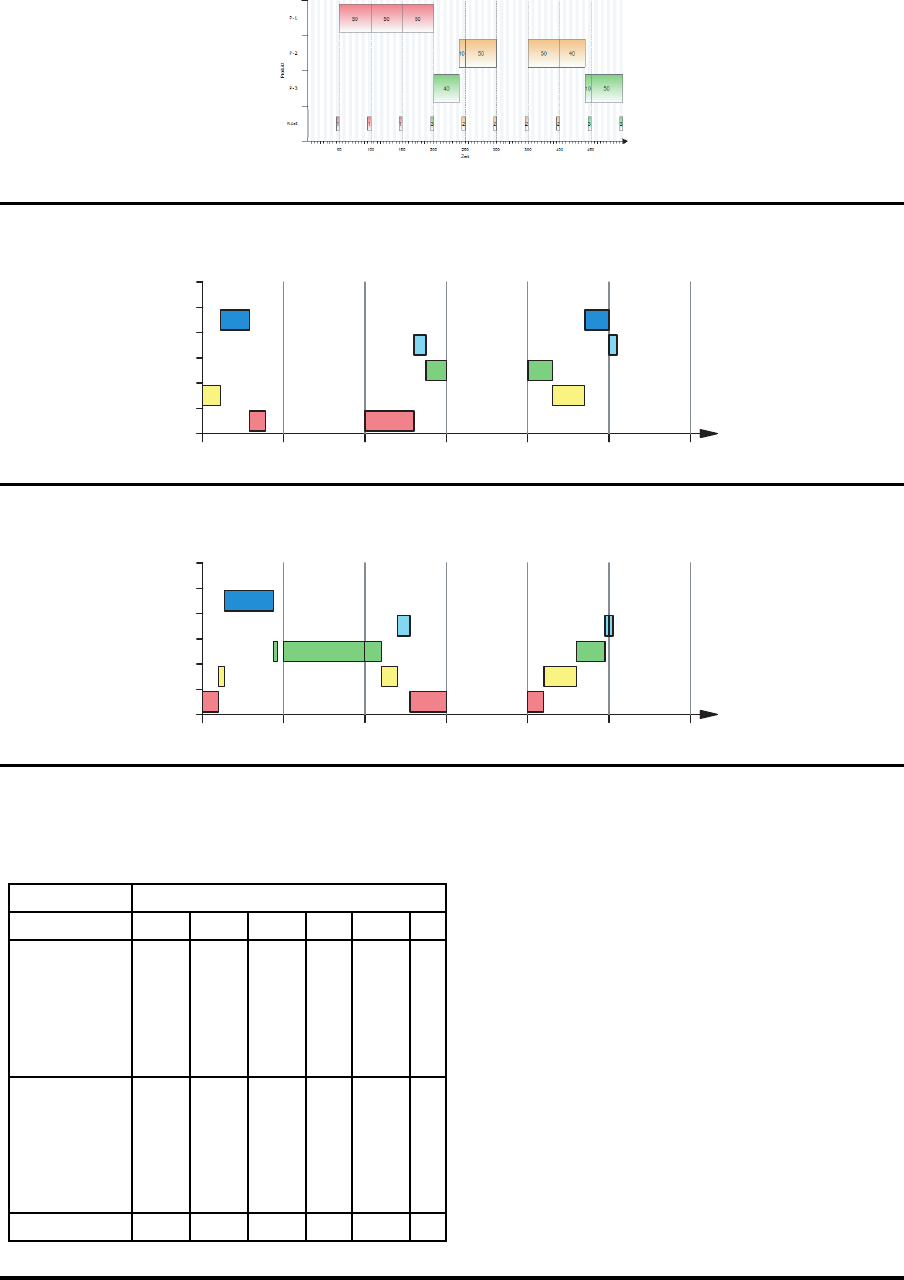
Modell CLSPL VI
0 200 400 600 800 1000 1200
P1
P2
P3
P4
P5
Z
10+30
0+120
10+35 10+70
10+40 0+60
10+20
10+10
10+60 10+50
1 1 3 3
Modell CLSPL VII
0 200 400 600 800 1000 1200
P1
P2
P3
P4
P5
Z
10+30 10+80 0+40
10+5 10+30 10+70
10+0 0+200 0+40 10+60
10+20 10+0 0+10
10+110
3 3 1 1 4
Modell CLSPL-A I
Optimale L¨osung de s Beispiels bei einmalig e r
¨
Ubertragung des R¨ustzustandes
Periode t
Produkt k 1 2 3 4 5 6
1 ✕❒ – ✕❒ ❒ – –
2 – – ✕❒ – ✕❒ –
3 – – ✕❒ ✕ ❒ –
4 – ✕❒ ❒ – – –
5 – ✕❒ – – ✕❒ –
1 30 – 80 40 – –
2 – – 30 – 70 –
3 – – 40 – 60 –
4 – 10 20 – – –
5 – 60 – – 50 –
Belastung 40 90 200 50 200 –
253
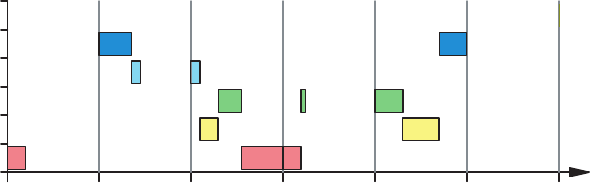
Modell CLSPL-A II
0 200 400 600 800 1000 1200
P1
P2
P3
P4
P5
Z
10+30 10+80 0+40
10+30 10+70
10+40 10+0 0+60
10+10 0+20
10+60 10+50
4 1 3
254
Modell CLSP-L-PM
SPL
Minimiere Z =
K
P
k=1
M
P
m=1
T
P
t=1
s
k
· γ
m
kt
+
K
P
k=1
M
P
m=1
T
P
t=1
T
P
τ =t
h
ktτ
· δ
m
ktτ
u. B. d. R.
M
P
m=1
τ
P
t=1
δ
m
ktτ
= 1 k = 1, 2, . . . , K; τ = 1, 2, . . . , T
δ
m
ktτ
≤ γ
m
kt
+ ω
m
kt
k = 1, 2, . . . , K; m = 1, 2, . . . , M
t = 1, 2, . . . , T ; τ = t, t + 1, . . . , T ; d
kτ
> 0
K
P
k=1
T
P
τ =t
tb
k
· d
kτ
·δ
m
ktτ
+ tr
k
· γ
m
kt
≤ b
m
t
m = 1, 2, . . . , M
t = 1, 2, . . . , T
K
P
k=1
ω
m
kt
≤ 1
m = 1, 2, . . . , M; t = 1, 2, . . . , T
ω
m
kt
≤ γ
m
k,t−1
+ ω
m
k,t−1
k = 1, 2, . . . , K; m = 1, 2, . . . , M
t = 1, 2, . . . , T
ω
m
kt
+ ω
m
k,t+1
≤ 1 + v
m
t
k = 1, 2, . . . , K; m = 1, 2, . . . , M
t = 1, 2, . . . , T − 1
v
m
t
+ γ
m
kt
≤ 1
k = 1, 2, . . . , K; m = 1, 2, . . . , M
t = 1, 2, . . . , T
ω
m
ˆ
k
m
1
= 1, ω
m
k1
= 0
k = 1, 2, . . . , K; k 6=
ˆ
k
m
; m = 1, 2, . . . , M
δ
m
ktτ
≥ 0
k = 1, 2, . . . , K; m = 1, 2, . . . , M
t = 1, 2, . . . , T ; τ = t, t + 1, . . . , T
γ
m
kt
, ω
m
kt
∈ {0, 1}
k = 1, 2, . . . , K; m = 1, 2, . . . , M
t = 1, 2, . . . , T
255
Modell CLSP-L-SD
SPL
Minimiere Z =
T
P
t=1
K
P
i=1
K
P
k=1
s
ik
· χ
ikt
+
K
P
k=1
T
P
t=1
T
P
τ =t
h
ktτ
·δ
ktτ
u. B. d. R.
τ
P
t=1
δ
ktτ
= 1 k = 1, 2, . . . , K; τ = 1, 2, . . . , T
δ
ktτ
≤
K
P
i=1
χ
ikt
+ ω
kt
k = 1, 2, . . . , K; t = 1, 2, . . . , T
τ = t, t + 1, . . . , T ; d
kτ
> 0
K
P
k=1
T
P
τ =t
tb
k
· d
kτ
·δ
ktτ
+
K
P
i=1
tr
ik
· χ
ikt
≤ b
t
t = 1, 2, . . . , T
K
P
k=1
ω
kt
= 1
t = 1, 2, . . . , T
ω
k,t+1
= ω
kt
+
K
P
i=1
χ
ikt
−
K
P
i=1
χ
kit
k = 1, 2, . . . , K
t = 1, 2, . . . , T
F
kt
≥ F
it
+ 1 − K · (1 − χ
ikt
)
i = 1, 2, . . . , K
k = 1, 2, . . . , K; k 6= i
t = 1, 2, . . . , T
ω
ˆ
k1
= 1, ω
k1
= 0
k = 1, 2, . . . , K; k 6=
ˆ
k
δ
ktτ
≥ 0 k = 1, 2, . . . , K; t = 1, 2, . . . , T ; τ = t, t + 1, . . . , T
ω
kt
≥ 0 k = 1, 2, . . . , K; t = 1, 2, . . . , T + 1
F
kt
≥ 0 k = 1, 2, . . . , K; t = 1, 2, . . . , T
χ
ikt
∈ {0, 1} i = 1, 2, . . . , K; k = 1, 2, . . . , K; t = 1, 2, . . . , T
Dabei bedeuten zus¨atzlich zu den bereits bekannten Symbolen:
χ
ikt
bin¨are Umr¨ustvariable vom R¨ustzustand i zum R¨ustzustand k in
Periode t
F
kt
Position des Produkts k in der R¨ustfolge der Periode t
ˆ
k Index des Produkts, f¨ur d as zu Beginn des Planungszeitraums ger¨ustet
worden ist
s
ik
R¨ustkostensatz f¨ur das Umr¨usten vom R¨ustzustan d i zum R¨ustzustand
k
256