
3
Teil XV
Operative Planung bei Sorten- bzw.
Fließproduktion
39 Statische Modelle der Losgr¨oßen- und Reihenfol-
geplanung
39.1 Einf¨uhrung
Zul¨assigkeit I
T · d
k
p
k
T
T
k
T
T
k
·τ
k
Zul¨assigkeit II
K
X
k=1
τ
k
·
T
T
k
+
d
k
p
k
· T
≤ T
K
X
k=1
τ
k
T
k
+
d
k
p
k
≤ 1
Zul¨assigkeit III
243
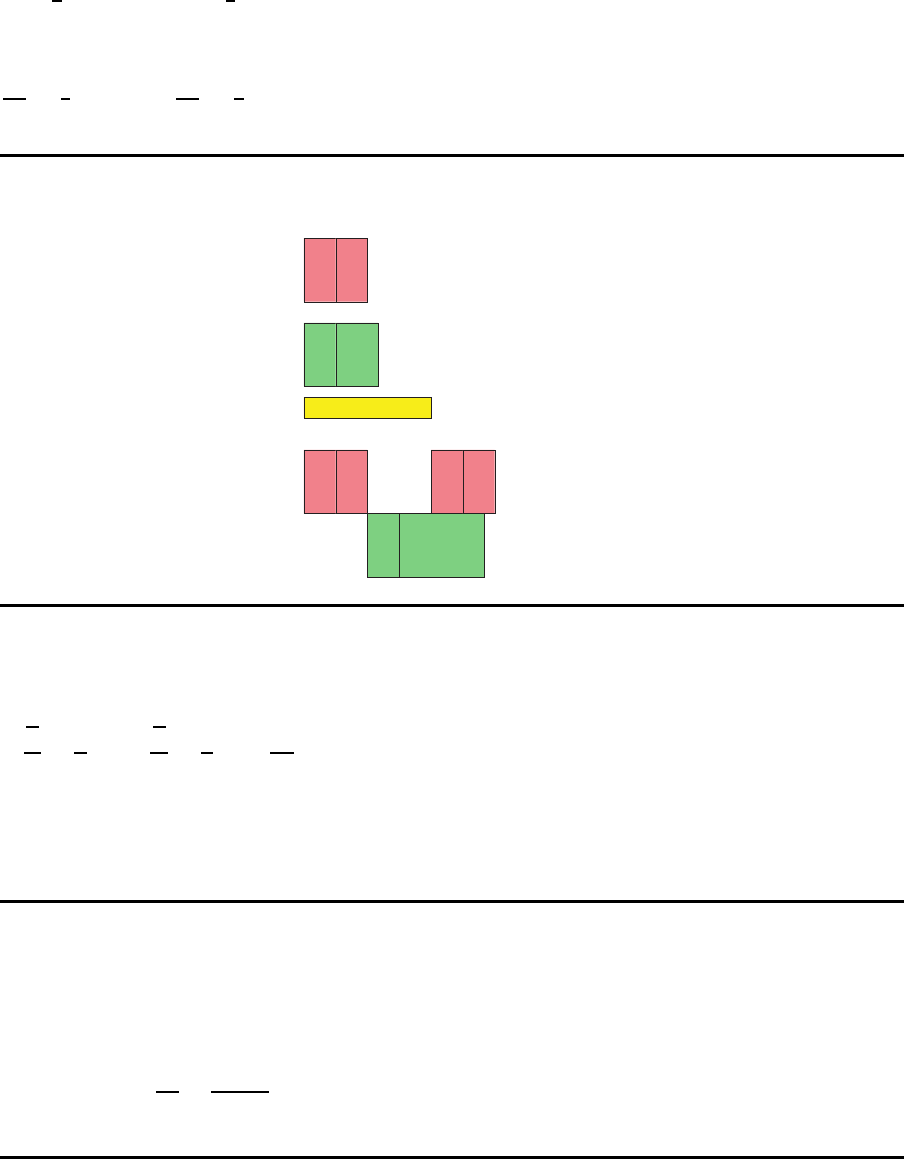
Produkt1 Produkt 2
T
1
= 1 T
2
= 2 Produktionszyklen
t
1
=
1
4
t
2
=
1
4
R¨ustzeiten
d
1
p
1
=
1
4
d
2
p
2
=
1
3
Zul¨assigkeit IV
τ=
1/4
d/p
=
1/4
τ=
1/4
d/p
=
1/3
τ=
1/4
d/p
=
1/4
τ=
1/4
2·d/p
=
2/3
τ=
1/4
d/p
=
1/4
Produkt 1
Produkt 2
Produkt 1
Produkt 2
T
Zul¨assigkeit V
1
4
1
+
1
4
+
1
4
2
+
1
3
=
23
24
39.2 Das ELSP
Identische Produktionszyklen I
T
k
= T k = 1, 2, ..., K
Min Z =
K
X
k=1
s
k
T
+
T · d
k
2
·h
k
· (1 − ρ
k
)
244

Identische Produktionszyklen II
T
opt
=
v
u
u
u
u
u
u
t
2 ·
K
P
k=1
s
k
K
P
k=1
h
k
· d
k
· (1 − ρ
k
)
q
k
= T
opt
·d
k
k = 1, 2, ..., K
Identische Produktionszyklen III
K
X
k=1
τ
k
+
d
k
· T
p
k
≤ T
K
P
k=1
τ
k
1 −
K
P
k=1
ρ
k
≤ T
Identische Produktionszyklen IV
k D
k
p
k
τ
k
s
k
h
k
1 4 150 18 5 0.000005
2 36 150 18 5 0.000005
3 25 150 18 5 0.000005
4 3 150 18 5 0.000005
5 2 150 18 5 0.000005
6 21 150 18 5 0.000005
7 9 150 18 5 0.000005
Identische Produktionszyklen V
T
min
=
126
1 − 0.666667
= 378 Minuten
T
opt
=
r
2 ·7 ·5
0.0004176
= 409.42
245
Isoliert optimale Losgr¨oßen
q
1
2866.91
q
2
9733.29
q
3
7745.97
q
4
2474.36
q
5
2013.47
q
6
6988.36
q
7
4375.95
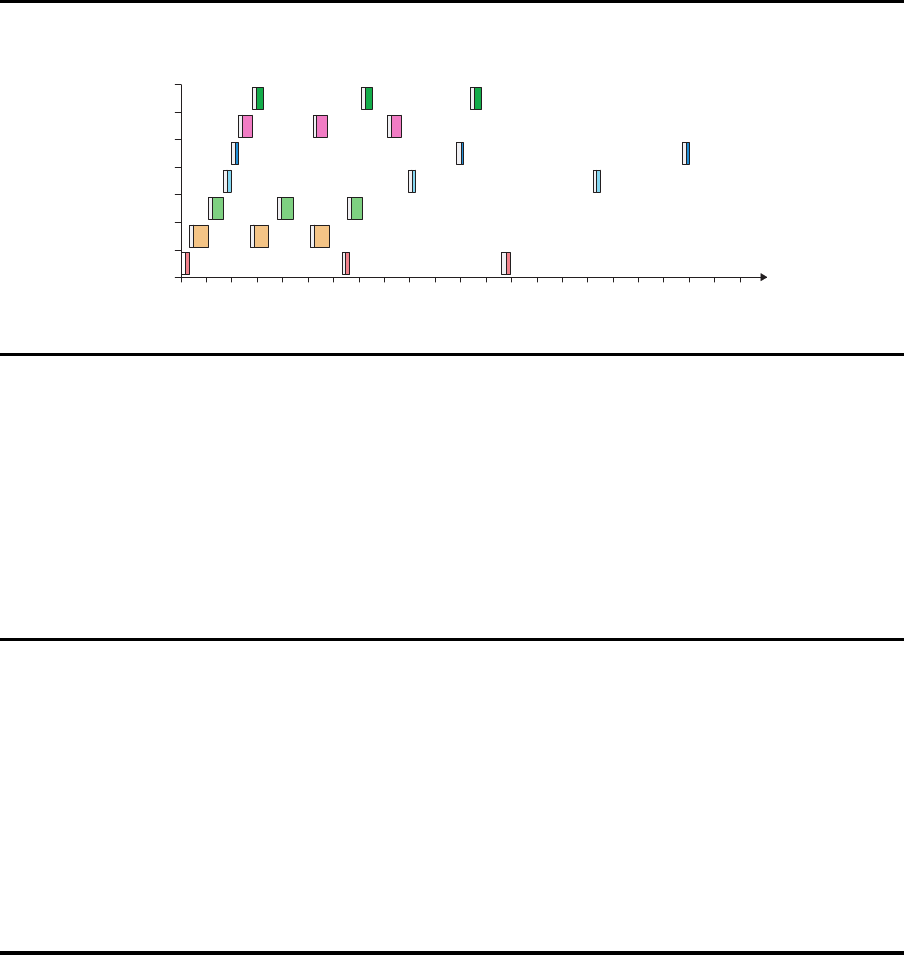
Isoliert optimale Losgr¨oßen: unzul¨assiger Produktionsplan
0 500 1000 1500 2000
1
2
3
4
5
6
7
Zeit
Produkt
Zwischenergebnisse
Summe der R¨ustzeiten: 126.000
Bearbeitungszeiten: 241.322
Belegungsdauer der Anlage: 367.322
Kosten dieser L ¨osung: 0.156
T
min
: 378.000
T
opt
: 409.420
Optimale Losgr¨oßen
q
1
409.420 · 4.00 = 1637.679
q
2
409.420 · 36.00 = 14739.110
q
3
409.420 · 25.00 = 10235.490
q
4
409.420 · 3.00 = 1228.259
q
5
409.420 · 2.00 = 818.839
q
6
409.420 · 21.00 = 8597.814
q
7
409.420 · 9.00 = 3684.778
246
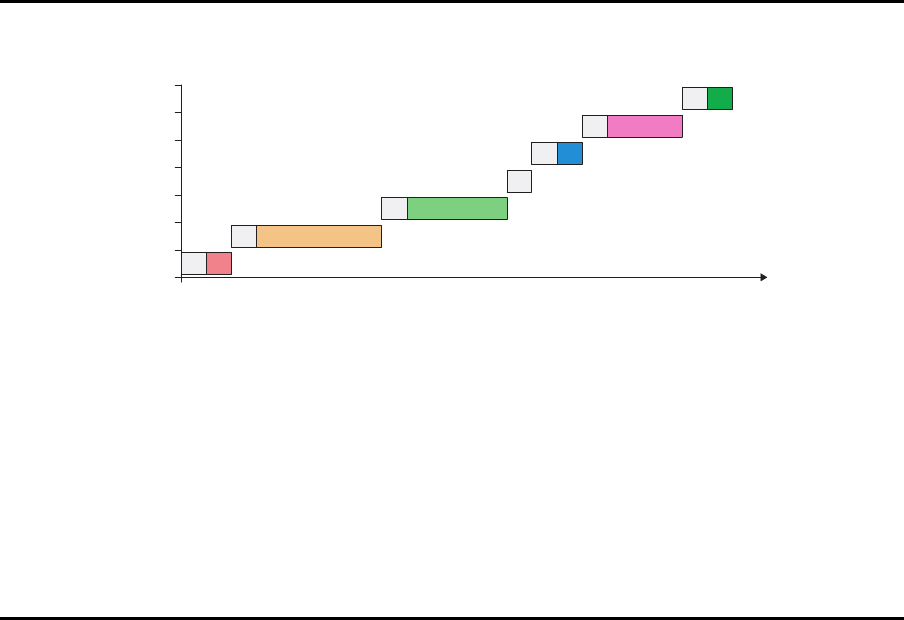
Ergebnisse
Kosten der opt ima len L¨osung: 0.171
Summe der R¨ustzeiten: 126.000
Bearbeitungszeiten: 272.947
Belegungsdauer der Anlage: 398.947
Leerzeit der Anlage pro Zyklus: 10.473
Zul¨assiger Produktionsplan
0
1
2
3
4
5
6
7
Zeit
Produkt
R 1
R 2
R 3
R4
R 5
R 6
R 7
40 Dynamische Modelle der Losgr ¨oßen- und Reih en-
folgeplanung
40.1 Einf¨uhrung
Literatur: Tempelmeier (2017), Abschnitt C.2.1.1.1
Modell C LSP
Modellformulierung
Minimiere Z =
K
X
k=1
T
X
t=1
s
k
· γ
kt
+ h
k
· y
kt
+ p
kt
· q
kt
u. B. d. R.
y
k,t−1
+ q
kt
− y
kt
= d
kt
k = 1, 2, . . . , K; t = 1, 2, . . . , T
q
kt
−M · γ
kt
≤ 0 k = 1, 2, . . . , K; t = 1, 2, . . . , T
247

K
X
k=1
tb
jk
·q
kt
+ tr
jk
· γ
kt
≤ b
jt
j = 1, 2, . . . , J; t = 1, 2, . . . , T
q
kt
≥ 0 k = 1, 2, . . . , K; t = 1, 2, . . . , T
Modell C LSP
SPL
Modellformulierung
Minimiere Z =
K
X
k=1
T
X
t=1
s
k
· γ
kt
+
K
X
k=1
T
X
t=1
T
X
τ =t
h
ktτ
· δ
ktτ
u. B. d. R.
τ
X
t=1
δ
ktτ
= 1 k = 1, 2, . . . , K; τ = 1, 2, . . . , T
δ
ktτ
≤ γ
kt
k = 1, 2, . . . , K; t = 1, 2, . . . , T ;
τ = t, t + 1, . . . , T ; d
kτ
> 0
X
k∈K
j
"
T
X
τ =t
tb
k
·d
kτ
· δ
ktτ
+ tr
k
· γ
kt
#
≤ b
jt
j = 1, 2, . . . , J;
t = 1, 2, . . . , T
δ
kτ t
≥ 0 k = 1, 2, . . . , K; τ = 1, 2, . . . , T ; t = τ, τ + 1, . . . , T
γ
kτ
∈ {0, 1} k = 1, 2, . . . , K; τ = 1, 2, . . . , T
Modell C LSP-P M
Modellformulierung
Minimiere Z =
K
X
k=1
M
X
m=1
T
X
t=1
s
k
· γ
m
kt
+ p
kt
· q
m
kt
+
K
X
k=1
T
X
t=1
h
k
· y
kt
248
u. B. d. R.
y
k,t−1
+
M
X
m=1
q
m
kt
− y
kt
= d
kt
k = 1, 2, . . . , K; t = 1, 2, . . . , T
q
m
kt
−M · γ
m
kt
≤ 0 k = 1, 2, . . . , K; m = 1, 2, . . . , M; t = 1, 2, . . . , T
K
X
k=1
tb
k
· q
m
kt
+ tr
k
·γ
m
kt
≤ b
m
t
m = 1, 2, . . . , M; t = 1, 2, . . . , T
q
m
kt
≥ 0 k = 1, 2, . . . , K; m = 1, 2, . . . , M; t = 1, 2, . . . , T
y
k0
= 0; y
kT
= 0 k = 1, 2, . . . , K
y
kt
≥ 0 k = 1, 2, . . . , K; t = 1, 2, . . . , T
γ
m
kt
∈ {0, 1} k = 1, 2, . . . , K; m = 1, 2, . . . , M; t = 1, 2, . . . , T
249