
6b
37 Nicht-identische Bearbeitungsreihenfo lgen
(Job shop)
Siehe zum Folgenden auch: A. C. Hax und D. Candea, Production and Inventory Man-
agement, Englewood Cliffs (Prentice-Hall), 1984, S. 314–321
Bei dynamischer und stochastischer Produktion, bei der M Werkst¨atten gemeinsam zu
planen sind, treffen Auftr¨age dynamisch in stochastischen Abst¨anden kontinuierlich im
Zeitablauf ein. Man nimmt i. a. a n, daß die Bearbeitungszeiten der Auftr¨age zum Zeit-
punkt ihres Eintreffen bekannt sind.
Vor jeder Werkstatt (ein Arbeitssystem oder eine Gruppe identischer Arbeitssysteme)
befindet sich eine Menge von Auftr¨agen (Warteschlange), die auf ihre Bearbeitung warten.
Nach seiner Bearbeitung wird ein Auftrag zur n¨achsten Werkstatt , die in seinem Arb eits-
plan verzeichnet ist, weitergeleitet und reiht sich dort in die Warteschlange ein.
Unter solchen Bedingungen kann man nicht mehr einen festen Ablaufplan erzeugen, in
dem f¨ur jeden Auftrag an jeder Maschine der Anfangs- und der Endtermin der Bear-
beitung festgelegt sind. Eine M¨oglichkeit besteht darin, das Problem in so viele dynami-
sche und stochastische Ein-Maschinen-Reihenfolgeprobleme zu zerlegen, wie es Werkst¨atten
gibt. An j eder Werkstatt erfolgt die Reihenfolgeplanung dann unter Verwendung einer
Priorit¨atsregel.
Damit stellt sich die Frage, welche Priorit¨atsregel man unter welchen Bedingungen ein-
setzen soll, wenn man ein bestimmtes Ziel verfolgt. Man hat a uf zwei Arten versucht,
Antworten auf diese Fra ge zu geben:
• durch analytische
¨
Uberlegungen auf der Grundlage der Warteschlangen-
theorie
• durch Simulationsstudien
Viele praxisrelevante Aussagen wurden aus Simulationsexperimenten abg eleitet. In einem
Simulationsmodell wird der Produktionsprozeß in einer Werkstatt realistisch abgebildet.
Man erzeugt einen hypothetischen Auftragsbestand, der mit sto chastischen Zwischenan-
kunftszeiten im Produktionsbereich eintrifft. Auch die Bearbeitungszeiten werden h¨aufig
als stochastische Gr¨o ßen vorgegeben.
Die Auftr¨age werden dann entsprechend den vorgegebenen Maschinenfolgen (Arbeits-
pl¨anen) durch die Werkst¨atten geschleust. W¨ahrend der Simulation werden die inter-
essierenden Informationen gesammelt und nach Ende des Simulationslaufs statistisch
ausgewertet.
Die meisten Simulationsstudien dienten zur Gewinnung von Informationen ¨uber Zielgr¨oßen,
die mit folgenden Gr¨oß en in Zusammenhang stehen:
234
Priorit¨atsregeln
• Staueffekte in der Werkstatt (hohe Lagerbest¨ande, la nge Wartezeiten, lange Durch-
laufzeiten)
• Termineinhaltung (Versp¨atungen, Terminabweichungen)
37.1 Priorit¨atsregeln zum Abbau von Staueffekten
In einer Werkstatt auftretende Staueffekte ¨a ußern sich in hohen Lagerbest¨anden und
in langen Durchlaufzeiten. Will man nur die mittlere Durchlaufzeit der Auftr¨age
minimieren, dann empfiehlt sich der Einsatz der K¨urzesten-Operatio nszeit-Regel (KOZ-
Regel). Bei Anwendung dieser Priorit¨atsregel wird aus der Menge der vor einer Maschine
wartenden Auftr¨age immer der Auftrag als n¨achster bearbeitet, der die k¨urzeste Bear-
beitungszeit an der betrachteten Maschine hat.
Diese Regel maximiert die Anzahl bearbeiteter Auftr¨age in einem gegebenen
Zeitraum und damit auch die mittlere Durchlaufzeit der Auftr¨age. Die KOZ-Regel hat
sich auch in komplexeren Netzwerken als g¨unstig im Hinblick auf die mittlere Durch-
laufzeit erwiesen. Als Nachteil der KOZ-Regel wird i. a. angesehen, daß Auftr¨age
mit langen Bearbeitungszeiten, z. B. gr¨oßere Lose, immer wieder nach hinten verschoben
werden. Das hat zur Folge, daß die mittlere D ur chlaufzeit zwar niedrig ist, die Varianz
der Durchlaufzeit aber groß ist. Um diesen Nachteil zu beheben, wurden folgende
Modifikationen vorgeschlagen:
• Simultane Anwendung
Ber¨ucksichtigung der Wartezeit eines Auftrags: die KOZ-Regel wird ange-
wandt, sofern die Auftr¨a ge eine bestimmte maximale Wartezeit nicht ¨uber-
schritten haben. Die Auft r¨age, die schon die maximale Wartezeit ¨uberschritten
haben, werden nicht nach der KOZ-Regel, sondern nach der FCFS-Regel
(First-come-first-served-Regel) bearbeitet. Diese Form der Kombination
von Priorit¨atsregeln kann man als simultane Anwendung bezeichnen.
• Abwechselnde Anwendung
Abwechselnde Anwendung der KOZ-Regel und der FCFS-Regel. Diese
Form der Kombination von Priorit¨atsregeln wurde in verschiedenen Vari-
anten eingesetzt:
• Situationsabh¨angige Anwendung der FCFS-Regel, bis
die Anzahl wartender Auftr¨age eine bestimmte Grenze ¨uberschreitet;
dann
¨
Ubergang zur KOZ-Regel, bis die Anzahl wartender
Auftr¨age eine bestimmte untere Grenze unterschritten hat;
dann wieder
¨
Ubergang zur FCFS-Regel.
• Regelm¨aßiger Wechsel zwischen KOZ-Regel und FCFS-
Regel (in einem festen zeitlichen Rhythmus).
235
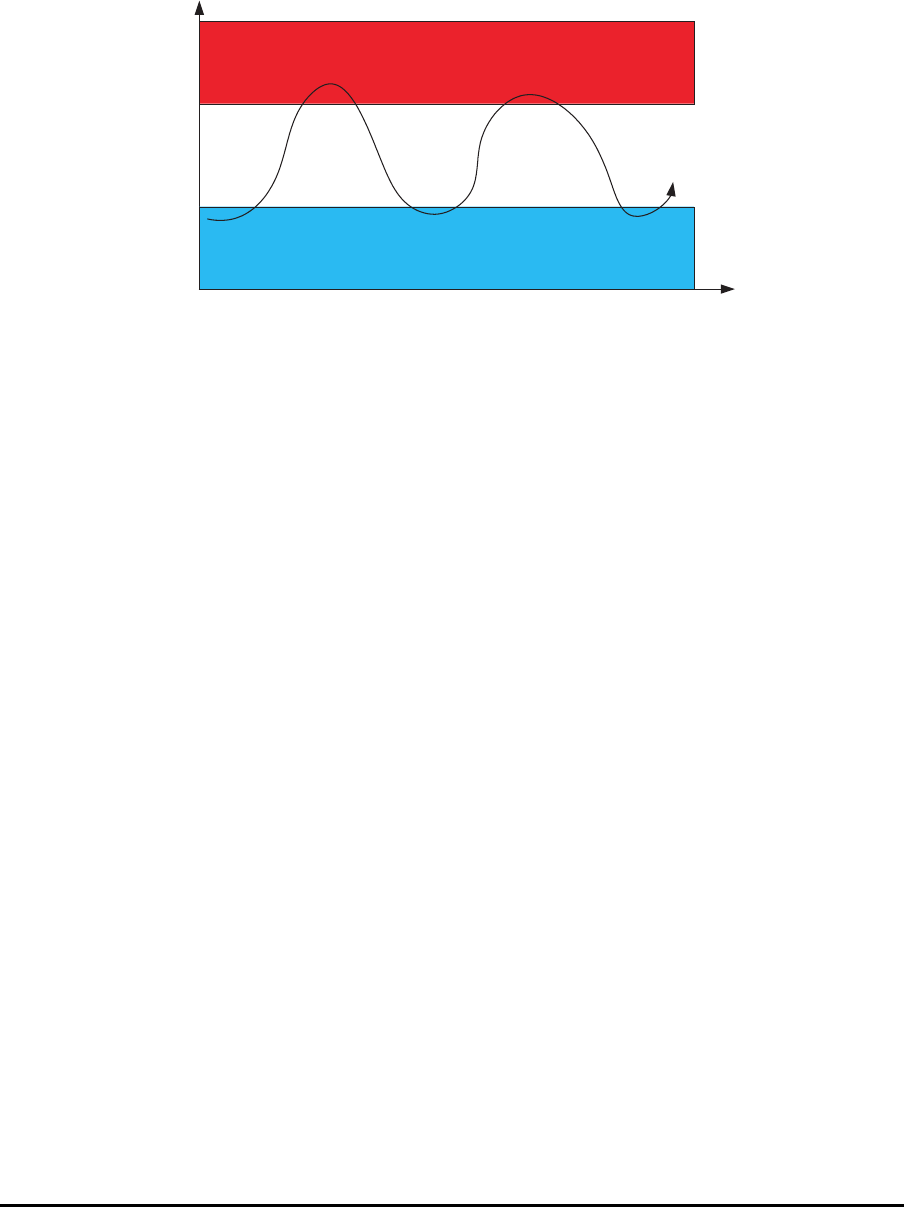
FCFS
KOZ
Anzahl wartender Aufträge
Zeit
Figure 1: Kombinierter Einsatz von KOZ- und FCFS-Regel
Diese kombinierten Prio r it ¨atsregeln sind allerdings nicht gleichwertig. So hat man fest-
gestellt, daß der abwechselnde Einsatz von KOZ-Regel und FCFS-Regel nur zu einem
vergleichsweise geringen Anstieg der mittleren Durchlaufzeit f¨uhrte, w¨ahrend bei der si-
multanen Anwendung von KOZ-Regel und FCFS-R egel ein starker Anstieg der mittleren
Durchlaufzeit zu verzeichnen war.
Da die genannten Priorit¨atsregeln lediglich auf Informationen zur¨uckgreifen, die eine
bestimmte Warteschlange bzw. Maschine betreffen, kann man sie auch als lokale Pri-
orit¨atsregeln bezeichnen. Im Gegensatz dazu verwenden globale Priorit¨atsregeln auch
Informationen, die von anderen Warteschlangen bzw. Maschinen stammen. Solche glob-
alen Priorit¨atsregeln sind die nat¨urliche Erweiterung der lokalen Priorit¨atsregeln bei
mehrstufiger Fertigung von Auftr¨agen in mehreren Arbeitsg¨angen an mehreren Maschi-
nen.
Zwei solche glo balen Priorit¨atsregeln sind
WINQ-Regel (Work in next queue): hier erh¨alt der Auftra g die h¨ochste Pri-
orit¨at, der nach Ablauf der Bearbeitung an der gerade betrachteten Mas-
chine zu der Maschine mit der kleinsten Warteschlange weitergeht.
EWINQ-Regel (Expected work in next queue): hier wird wie oben vorgegangen;
nur wird bei der Bestimmung der L¨ange der Warteschlange an der n¨achsten
Maschine auch noch der erwartete Auftragsz uga ng bis zu dem e rwarteten
Eintreffen des aktuellen Auftrags ber¨ucksichtigt.
Diese beiden Priorit¨atsregeln sind mit Hilfe eines Leitstands bzw. durch die neuen M¨oglichkeiten
von Industrie 4.0 einsetzbar. Simulationsergebnisse zeigen, daß beide Priorit¨atsregeln im
Hinblick auf die mittlere Anzahl wartender Auftr¨age schlechter sind als die KOZ-Regel.
Durch lineare Kombination dieser Regeln mit der KOZ-Regel konnten ab er geringf¨ugige
Verbesserungen festgestellt werden, wie die folgende Tabelle zeigt.
Bestandsorientierte Regeln
Simulationsergebnisse
236

Priorit¨atsregel Mittlere Anzahl wartender Auftr¨a ge
KOZ 23.25
WINQ 40.43
XWINQ 34.03
0.5 · KOZ + 0.5 · WINQ 30.14
0.9 · KOZ + 0.1 · WINQ 23.76
0.95 · KOZ + 0.05 · WINQ 23.00
0.97 · KOZ + 0.03 · WINQ 22.83
0.94 · KOZ + 0.06 ·XWINQ 23.26
0.96 · KOZ + 0.04 ·XWINQ 22.67
0.98 · KOZ + 0.02 ·XWINQ 22.74
37.2 Priorit¨atsregeln zur Einhaltung von Terminen
Die Einhaltung von Terminen wird durch die H¨aufigkeitsverteilung der Termin¨uberschrei-
tungen oder durch die H¨aufigkeitsverteilung der Terminabweichungen beschrieben. Auch
positive Terminabweichungen (zu fr¨uhe Fertigstellungen) k¨onnen ja unerw¨unscht sein,
weil dadurch Kapital zu fr¨uh gebunden wird.
Auch zur Untersuchung der Leistungsf¨ahigkeit von Priorit¨atsregeln im Hinblick auf die
Termineinhaltung wurden Simulationsstudien durchgef¨uhrt. Dabei erweist es sich jedoch
als problematisch, wie man die Liefertermine realisisch bestimmen soll. In der Pra xis
werden diese ja entweder von Kunden oder von der Produktionsplanung festgelegt.
In einer Simulationsstudie wurden folgende Priorit¨a t sregeln untersucht, in denen Infor-
mationen ¨uber die (vorgegebenen) Liefertermine verarbeitet werden:
Lieferterminregel (DDATE): hier erh¨alt der Auftrag die h¨ochste Priorit¨at,
dessen Liefertermin am n¨achsten ist.
Schlupfzeitregel (SLACK): hier erh¨alt der Auftrag die h¨ochste Priorit¨at, f¨ur
den die Differenz aus dem Liefertermin und dem aktuellen Da tum abz¨uglich
der noch verbleibenden Bearbeitungszeiten am geringsten ist.
Schlupf pro Bearbeitungsvorgang-Regel (SLACK/OPN) : hier erh¨alt der
Auftrag die h¨ochste Prior it¨at, f¨ur den der Quotient aus Schlupfzeit und
Anzahl noch verbleib ender Bearbeitungsvorg¨ange minimal ist.
In einem Vergleich dieser Priorit¨atsregeln kam Conway zu folgendem Ergebnis:
Terminorientierte Regeln
Simulationsergebnisse
237
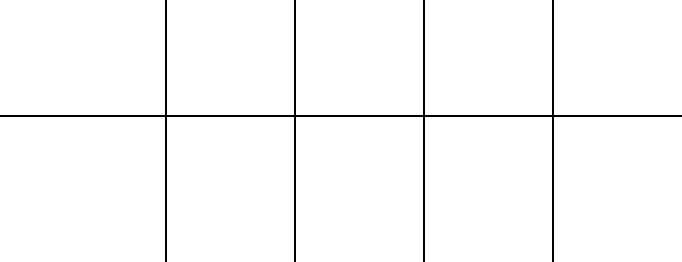
Priorit¨atsregel Anzahl
Auftr¨age
mit
Versp¨atung
mittlere
Terminab-
weichung
Varianz der
Terminab-
weichung
mittlere
Durch-
laufzeit
Liefertermin 15.75% -15.5 432 63.7
Schlupfzeit 22.02% -13.1 433 65.8
Schlupf-pro-AG 3.71% -12.8 266 66.1
KOZ 5.02% -44.9 2878 34.0
FCFS 44.79% -4.5 1686 74.4
In der obigen Tabelle g ing es um eine Werkstatt mit 9 Maschinen, durch die 8700 Auftr¨age
geschleust wurden. Die Liefertermine wurden in der Simulation proportional zur Gesamt-
bearbeitungszeit eines Auftra gs festgesetzt. Einige Anmerkungen zu den Ergebnissen:
• KOZ-Regel:
Die mittlere Terminabweichung ist sehr hoch, d. h. die die Auftr¨age werden zu fr¨uh fertig;
das liegt darin, daß mit der KOZ-Regel die mittlere D urchlaufzeit reduziert wird. D ie
negative Folge dieser Priorit¨atsregel sind hohe Lagerbest¨ande wegen zu fr¨uher Fertigstel-
lung. Die Varianz der Terminabweichung ist erheblich, da die KOZ- Regel nicht auf die
Termineinhaltung abzielt.
Man erkennt auch, daß nur wenige Auftr¨age zu sp¨at fertiggestellt werden.
• Schlupf-pro-AG-Regel (SLACK/OP N):
Diese Regel f¨uhrt, wie man sieht, zu einer wesentlich genaueren Termineinhaltung.
238

38 Zusammenhang zwischen Losgr¨oße und Durch-
laufzeit
38.1 Das Modell von Karmarkar
Das Verhalten eines Werkstattfertigungssystems wird zu einem großen Teil durch die
verwendete Losgr¨oßenpolitik beeinflußt.
Zur Absch¨atzung des Leistungsverhaltens von konventionellen Werkstattfertigungssyste-
men wurden von Karmarkar und Kekre verschiedene Modellierungsans¨atze vorgeschla-
gen. Kern dieser Ans¨atze ist die Annahme, daß die Durchlaufzeiten und Wartezeiten der
Auftr¨age in einem Werkstattfertigungssystem zu wesentlichen Teilen von den Losgr¨oßen
f¨ur die einzelnen Produkte abh¨a ngen, w¨a hr end den in der Ablaufplanung eingesetzten
Priorit¨atsregeln eine geringere Bedeutung zukommt. Die Warteph¨ano mene werden unter
Verwendung von Ergebnissen aus der Warteschlangentheorie analysiert.
Annahmen: M/M/1-Modell
• station¨are Situatio n
• exponentialverteilte Zwischenankunftszeiten von Auftr¨agen
• exponentialverteilte Bearbeitungszeiten
• ein Server (Maschine)
• unbegrenzter Warteraum vor der Maschine
Siehe auch Tempelmeier (2018), Aufgabe C4.1
Das Modell von Karmarkar
Symbole
τ R¨ustzeit
Q Losgr¨oße
P mittlere Produk tionsrate
D mittlere Ankunftsrate von Werkst¨ucken
λ mittlere Ankunftsrate
µ mittlere Abfertigungsrate
239
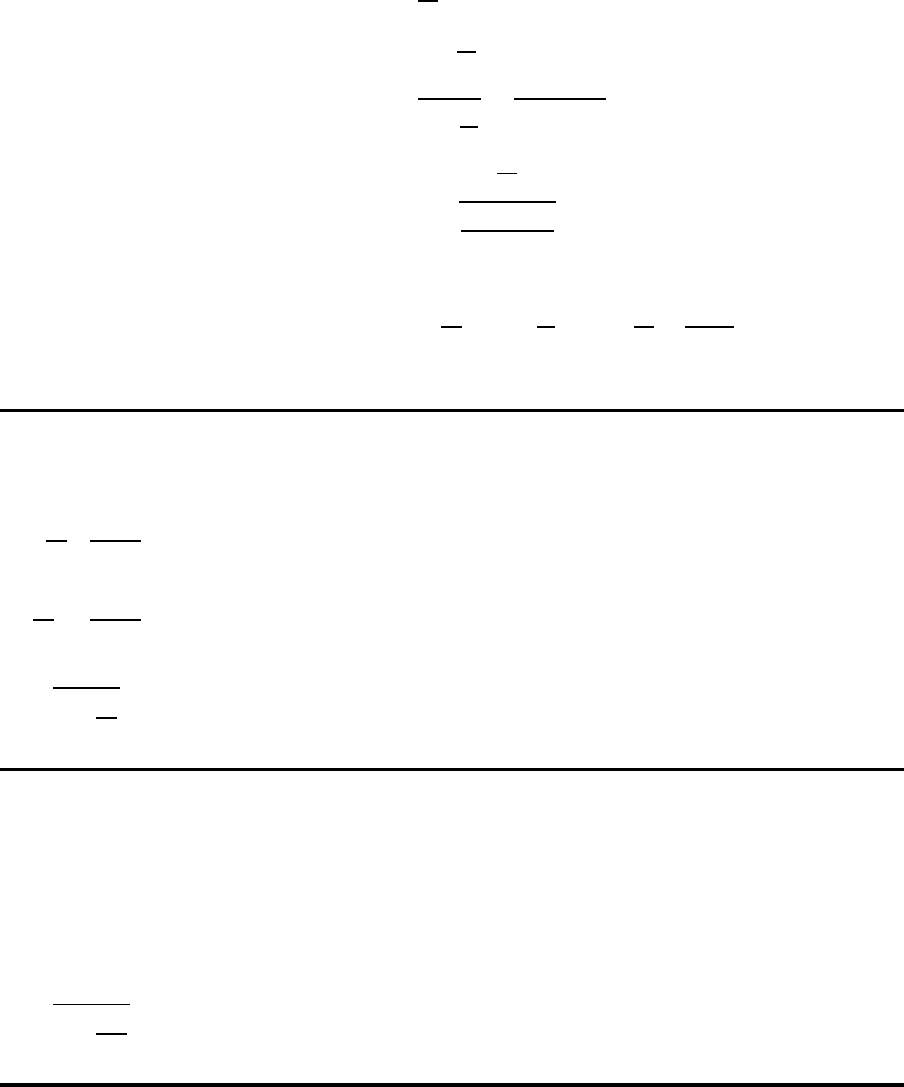
Karmarkar’s Modell I
Ankunftsrate von Losen:
D
Q
Bearbeitungszeit eines Loses: τ +
Q
P
mittlere Abfertigungsrate von Losen:
1
τ +
Q
P
=
P
τ · P + Q
Verkehrsintensit¨at: ρ =
D
Q
P
τ · P + Q
=
=
D
P
·
1 +
P
Q
· τ
=
D
P
+
D · τ
Q
Karmarkar’s Modell II
ρ =
D
P
+
D · τ
Q
< 1
1−
D
P
>
D · τ
Q
Q >
D · τ
1 −
D
P
Karmarkar’s Modell III
D = 1.5 ; τ = 1; P = 2
Q >
1.5 · 1
1 −
1.5
2
= 6
Karmarkar’s Modell IV
240
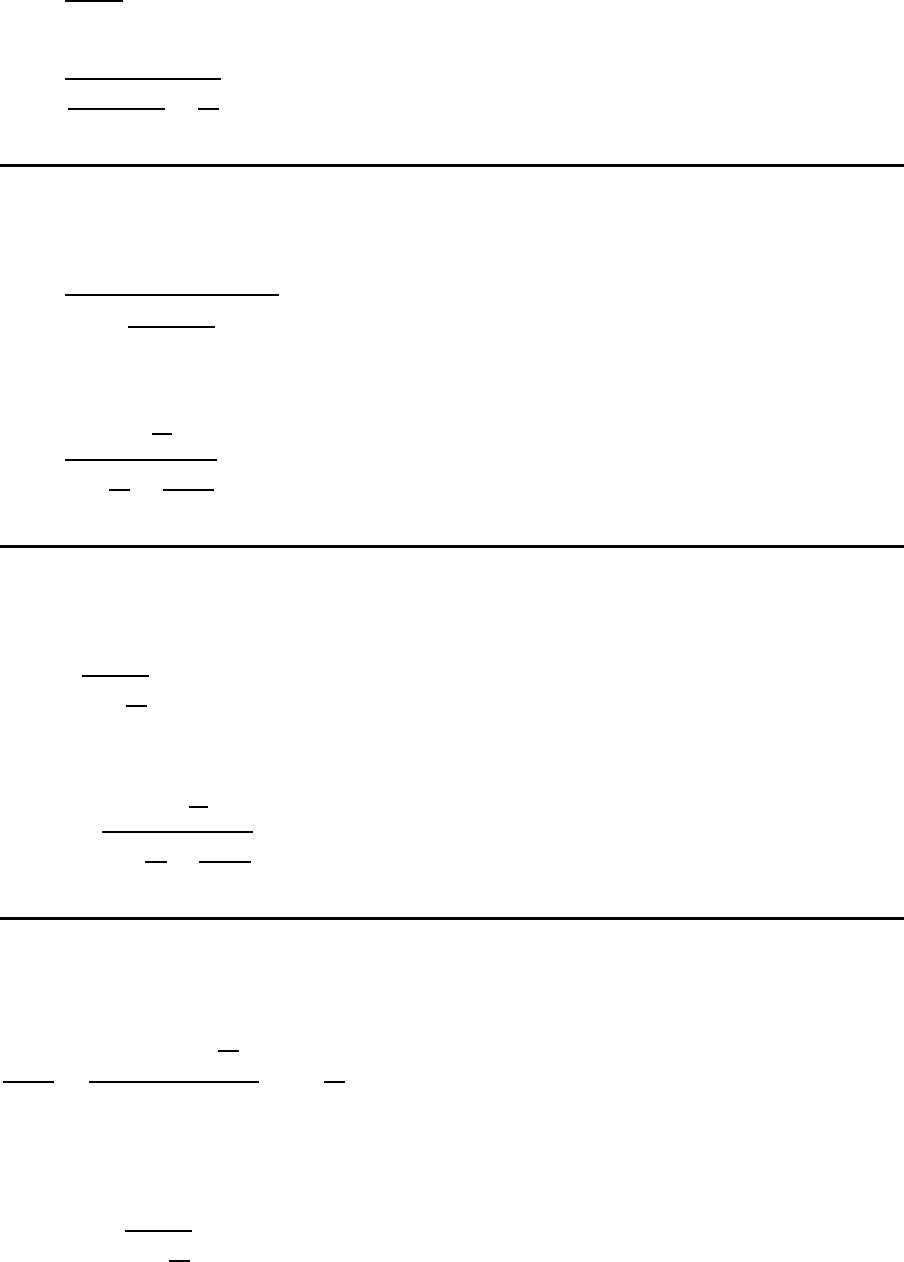
W
s
=
1
µ − λ
W
s
=
1
P
τ ·P + Q
−
D
Q
Karmarkar’s Modell V
W
s
=
τ · P + Q
P −
D · τ · P
Q
+ D
W
s
=
τ +
Q
P
1 −
D
P
−
D · τ
Q
Karmarkar’s Modell VI
Q
min
=
D · τ
1 −
D
P
W
s
(Q) =
τ +
Q
P
1 −
D
P
−
D · τ
Q
Karmarkar’s Modell VII
D · τ
Q
min
=
D · τ ·
1 −
D
P
D · τ
= 1−
D
P
lim W
s
(Q)
Q→Q
min
=
D · τ
1 −
D
P
= ∞
241
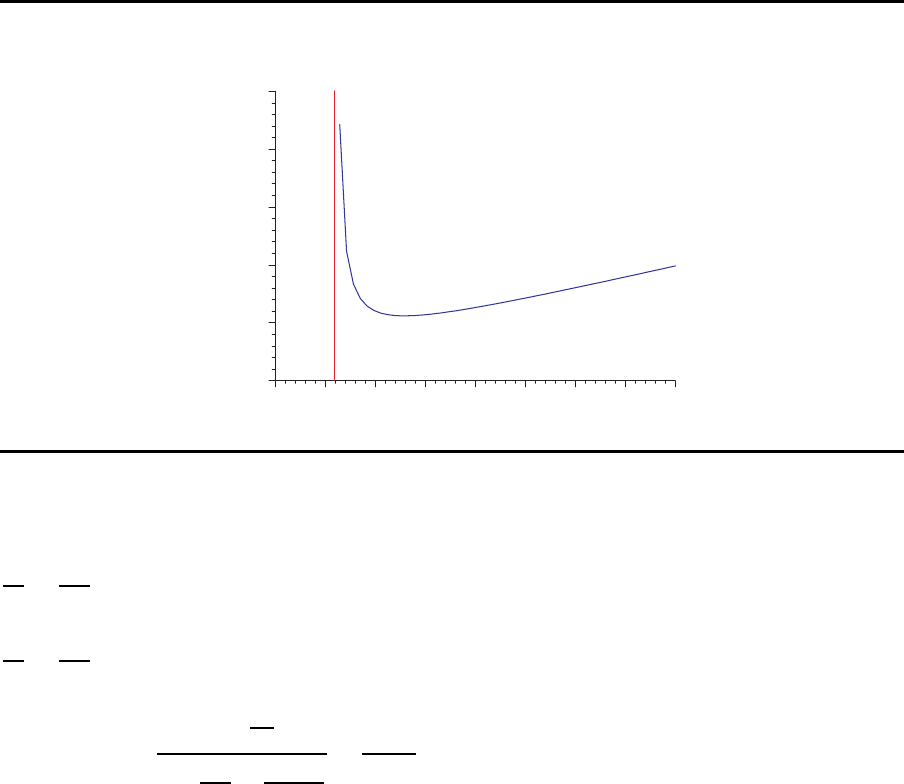
Losgr¨oße und mittlere Durchlaufzeit
0
50
100
150
200
250
Durchlaufzeit
0 5 10 15 20 25 30 35 40
Losgröße
Beispiel
D
P
=
1.5
2
= 0.75
D
Q
=
1.5
12
= 0.125
W
s
(Q = 12) =
1 +
12
2
1 −
1.5
2
−
1.5 · 1
12
=
7
0.125
= 56
242