2
23 Modell 2 – Eine Fabrik, Fremdlieferanten
23.1 Annahmen
Modell 2: Eine Fabrik, Fremdlieferanten
Annahmen
• Eine Fabr ik s ∈ S = {1}.
• Mehrere (End-)Produktgruppen k ∈ K
s
.
• T Perioden (Wochen, Monate, Quartale).
• Produktsp ezifische Nachfr age je Fabrik. Keine Modellierung der Kundenstandorte.
• Produktsp ezifische Fremdlieferanten, bei denen die Produkte bezogen werden
k¨onnen.
• Z ielfunktion: Lagerkosten,
¨
Uberstundenkosten, Beschaffungskosten, variable Pro-
duktionskosten
23.2 Modellformulierung
167

Zielfunktion
Min Z =
P
s∈ S
P
k∈K
s
T
P
t=1
l
s
k
· L
s
kt
| {z }
Lagerkosten
+ c
p
sk
· X
s
kt
| {z }
variable
Produktions-
kosten
+ c
b
sk
· B
s
kt
| {z }
Beschaffungs-
kosten
+
P
s∈ S
T
P
t=1
u
s
t
· U
s
t
| {z }
Kosten f¨ur
¨
Uberstunden
Lagerbilanzgleichung
L
s
k,t−1
| {z }
Anfangsbestand
+ X
s
kt
|{z}
Produktions-
menge
+ B
s
kt
|{z}
Fremdbezugs-
menge
− L
s
kt
|{z}
Endbestand
= d
s
kt
|{z}
Nachfrage
s ∈ S; k ∈ K
s
; t = 1, 2, ..., T
Produktionsmengenbeschr¨ankung f¨ur die technische Kapazit¨at
P
k∈K
s
b
s
k
· X
s
kt
| {z }
technischer
Kapazit¨ats-
bedarf
≤ C
s,max
t
| {z }
technische
Kapazit¨at
s ∈ S; t = 1, 2, ..., T
Produktionsmengenbeschr¨ankung f¨ur die personelle Kapazit¨at
P
k∈K
s
a
s
k
· X
s
kt
| {z }
gesamter
Personalbedarf
− U
s
t
|{z}
¨
Uberstunden
≤ N
s,max
t
| {z }
verf¨ugbare Nor-
malarbeitszeit
s ∈ S; t = 1, 2, ..., T
168

Maximale
¨
Uberstunden
U
s
t
≤ U
s,max
t
| {z }
maximale
¨
Uberstunden
s ∈ S; t = 1, 2, ..., T
Symbole I
Daten:
a
s
k
Produ k tionskoeffizient f¨ur Produktty p k in bezug auf die personelle
Kapazit¨at am S tandort s
b
s
k
Produ k tionskoeffizient f¨ur Produktty p k in bezug auf die technische
Kapazit¨at am S tandort s
c
b
sk
Fremdbezugskosten
c
p
sk
variable Produktionskosten bei Eigenproduktion
C
s,max
t
technische Kapazit¨at in Periode t am Standort s
d
s
kt
Nachfrage f¨ur Produkttyp k in Periode t am Standort s
Symbole II
Daten:
l
s
k
Lagerkostensatz f¨ur Produkttyp k pro Mengeneinheit und Periode am
Standort s
N
s,max
t
personelle Kapazit¨at am Standort s in Periode t
U
s,max
t
maximale personelle Zusatzkapazit¨at am Standort s in Periode t
u
s
t
Kosten f¨u r eine Einheit zus¨atzlicher personeller Kapazit¨at am
Standort s
Symbole III
Variablen:
B
kt
Beschaffungsmenge von Produkttyp k am Standort s in Period e t
L
s
kt
Lagerbestand f¨ur Produkttyp k am Standort s am Ende von Periode t
U
s
t
genutzte personelle Zusatzkapazit¨at am Standort s in Periode t
X
s
kt
Produ k tionsm enge von Produkttyp k am Standort s in Periode t
169
24 Modell 3 – Mehrere Fabriken
24.1 Annahmen
Modell 3: Mehrere Fabriken
Annahmen
• Mehrere Fabriken. s ∈ S = {1 , 2}. Tr ansporte zwischen den Fabriken.
• Mehrere (End-)Produktgruppen k ∈ K
s
.
• T Perioden ( Wochen, Monate, Quartale).
• Produktspezifische Na chfrage je Fabrik.
• Produktionsprogramm (Menge K
s
) je Fabrik.
• Z ielfunktion: Lagerkosten,
¨
Uberstundenkosten, Transport kosten.
Literaturhinweis
Tempelmeier (20 18), Aufgabe B1.4
24.2 Modellformulierung
170
Zielfunktion
Min Z =
P
s∈ S
P
k∈K
T
P
t=1
l
s
k
· L
s
kt
| {z }
Lagerkosten
+
P
s∈ S
T
P
t=1
u
s
t
· U
s
t
| {z }
Kosten f¨ur
¨
Uberstunden
+
T
P
t=1
Perioden
P
k∈K
Produkte
P
s∈ S
von Fabrik
P
i∈ S
nach Fabrik
f
si
k
· F
si
kt
| {z }
Transport”-
kosten
Lagerbilanzgleichung
L
s
k,t−1
| {z }
Anfangsbestand
+
X
i∈ S
F
is
kt
| {z }
Zufluß aus den
anderen
Fabriken
−
X
j∈ S
F
sj
kt
| {z }
Abfluß in die
anderen
Fabriken
+ X
s
kt
|{z}
Produktions-
menge
− L
s
kt
|{z}
Endbestand
= d
s
kt
|{z}
Nachfrage
s ∈ S; k ∈ K
s
; t = 1, 2, ..., T
Produktionsmengenbeschr¨ankung f¨ur die technische Kapazit¨at
P
k∈K
s
b
s
k
· X
s
kt
| {z }
technischer
Kapazit¨ats-
bedarf
≤ C
s,max
t
| {z }
technische
Kapazit¨at
s ∈ S; t = 1, 2, ..., T
Produktionsmengenbeschr¨ankung f¨ur die personelle Kapazit¨at
P
k∈K
s
a
s
k
· X
s
kt
| {z }
gesamter
Personalbedarf
− U
s
t
|{z}
¨
Uberstunden
≤ N
s,max
t
| {z }
verf¨ugbare Nor-
malarbeitszeit
s ∈ S; t = 1, 2, ..., T
171

maximale
¨
Uberstunden
U
s
t
≤ U
s,max
t
| {z }
maximale
¨
Uberstunden
s ∈ S; t = 1, 2, ..., T
Symbole I
Daten
a
s
k
Produ k tionskoeffizient f¨ur Produktty p k in bezug auf die personelle
Kapazit¨at am S tandort s
b
s
k
Produ k tionskoeffizient f¨ur Produktty p k in bezug auf die technische
Kapazit¨at am S tandort s
C
s,max
t
technische Kapazit¨at in Periode t am Standort s
d
s
kt
Nachfrage f¨ur Produkttyp k in Periode t am Standort s
f
si
k
Transportkostensatz f¨ur Produkttyp k pro Mengeneinheit vom Standort
s zum Standort i
K Menge aller Produkte (aus allen Fabriken)
l
s
k
Lagerkostensatz f¨ur Prod ukttyp k pro Mengeneinheit am Standort s
N
s,max
t
personelle Kapazit¨at am Standort s in Periode t
U
s,max
t
maximale personelle Zusatzkapazit¨at am Standort s in Periode t
u
s
t
Kosten f¨u r eine Einheit zus¨atzlicher personeller Kapazit¨at am
Standort s
Symbole II
Variablen
L
s
kt
Lagerbestand f¨ur Produkttyp k am Standort s am Ende von Periode t
U
s
t
genutzte personelle Zusatzkapazit¨at am Standort s in Periode t
X
s
kt
Produ k tionsm enge von Produkttyp k am Standort s in Periode t
F
si
kt
Transportmenge des Produkttyps k vom Standort s zu m Standort i in
Periode t
172
25 Modell 4 – Mehrere Fabriken, Fremdlieferanten
25.1 Annahmen
Modell 4: Mehrere Fabriken, Fremdlieferanten
25.2 Modellformulierung
Zielfunktion
Min Z =
P
s∈ S
P
k∈K
s
T
P
t=1
h
l
s
k
· L
s
kt
| {z }
Lagerkosten
+ c
p
sk
· X
s
kt
| {z }
variable
Produktions”-
kosten
+ c
b
sk
· B
s
kt
| {z }
Beschaffungs-
kosten
i
+
P
s∈ S
T
P
t=1
u
s
t
· U
s
t
| {z }
Kosten f¨ur
¨
Uberstunden
+
T
P
t=1
Perioden
P
k∈K
Produkte
P
s∈ S
von Fabrik
P
i∈ S
nach Fabrik
f
si
k
· F
si
kt
| {z }
Transport-
kosten
Lagerbilanzgleichung
173
L
s
k,t−1
| {z }
Anfangsbestand
+
X
i∈ S
F
is
kt
| {z }
Zufluß aus den
anderen
Fabriken
−
X
j∈ S
F
sj
kt
| {z }
Abfluß in die
anderen
Fabriken
+ X
s
kt
|{z}
Produktions-
menge
+ B
s
kt
|{z}
Fremdbezug
− L
s
kt
|{z}
Endbestand
= d
s
kt
|{z}
Nachfrage-
menge
s ∈ S; k ∈ K
s
; t = 1, 2, ..., T
Produktionsmengenbeschr¨ankung f¨ur die technische Kapazit¨at
P
k∈K
s
b
s
k
· X
s
kt
| {z }
technischer
Kapazit¨ats-
bedarf
≤ C
s,max
t
| {z }
technische
Kapazit¨at
s ∈ S; t = 1, 2, ..., T
Produktionsmengenbeschr¨ankung f¨ur die personelle Kapazit¨at
P
k∈K
s
a
s
k
· X
s
kt
| {z }
gesamter
Personalbedarf
− U
s
t
|{z}
¨
Uberstunden
≤ N
s,max
t
| {z }
verf¨ugbare Nor-
malarbeitszeit
s ∈ S; t = 1, 2, ..., T
maximale
¨
Uberstunden
U
s
t
≤ U
s,max
t
| {z }
maximale
¨
Uberstunden
s ∈ S; t = 1, 2, ..., T
Mindestbestand je Produkt
174
L
s
kt
≥ L
s,min
kt
|{z }
Mindestbestand
s ∈ S; k ∈ K
s
; t = 1, 2, ..., T
Lagerkapazit¨at
X
k∈K
s
L
s
kt
| {z }
Gesamter
Lagerbestand
≤ L
s,max
t
s ∈ S; t = 1, 2, ..., T
175
Teil XI
Aggregierte Gesa mtplanung –
Mehrstufige Probleme
26 Mehrstufige Probleme - Einf¨uhrung
Literaturhinweis
Tempelmeier (20 17), Kapitel B.2
26.1
¨
Ubersicht
¨
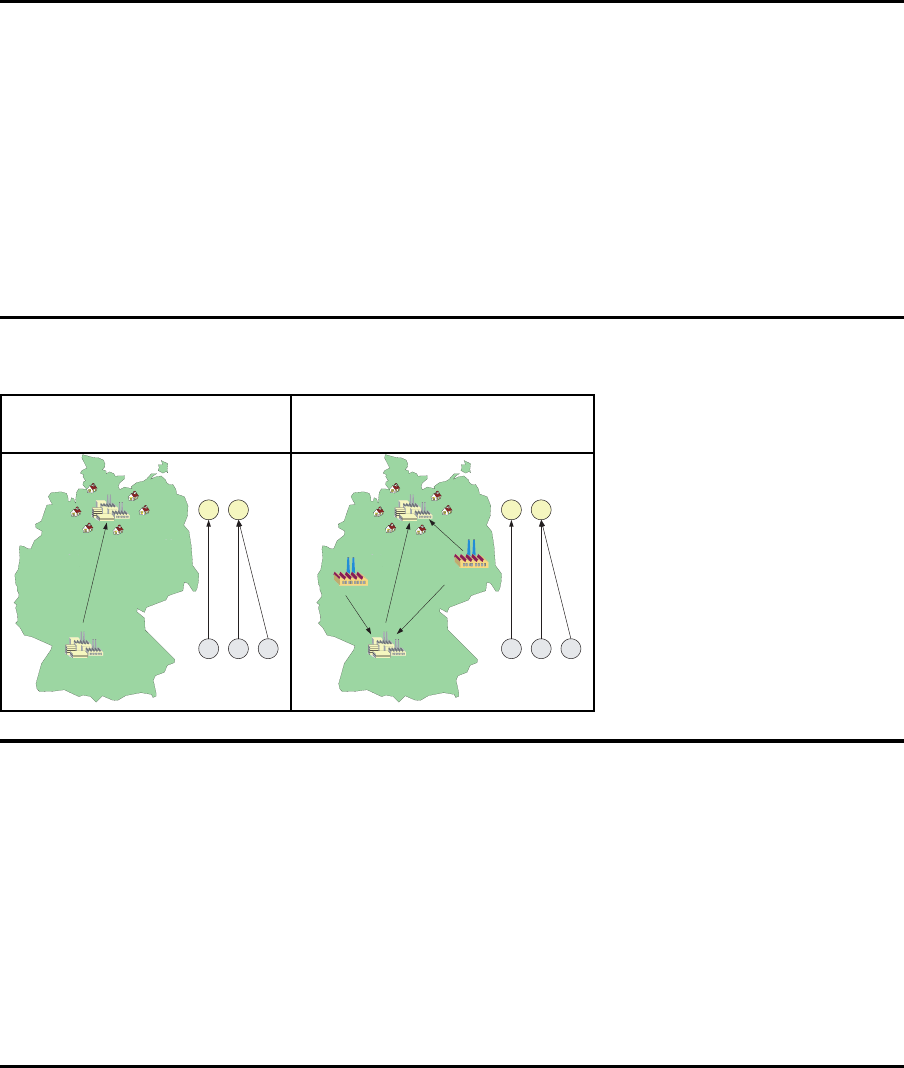
Ubersicht
Mehrere Fabriken Mehrere Fabriken
Lieferanten
Vorprodukte
(Fabrik 2)
Endprodukte
(Fabrik 1)
1 2
a b c
Erzeugnisstruktur
Vorprodukte
(Fabrik 2)
Endprodukte
(Fabrik 1)
1 2
a b c
Erzeugnisstruktur
Lieferanten
Vorprodukte
Endprodukte
Lieferanten
Vorprodukte
Materialflußmatrix
Q =
0 0 0
0 0 0
1 1 0
27 Modell 5 – Mehrstufige Produkt ion
27.1 Annahmen
• mehrere Fabriken (unterschiedliche Produktionsstufen)
176
• mehrere Produkte
• Produktionsstufe 1 liefert an Produktionsstufe 2
Literaturhinweis
Tempelmeier (20 18), Aufgabe B1.5
27.2 Modellformulierung
Ge¨anderte Lagerbilanzgleichungen
L
s
k,t−1
| {z }
Anfangsbestand
+ X
s
kt
|{z}
Produktions-
menge
−
Sekund¨ar-
bedarf
z }| {
X
j∈K
Nachfolge-
produkte
q
kj
|{z}
Direktbedarfs
koeffizient
·X
s
jt
− L
s
kt
|{z}
Endbestand
= d
s
kt
|{z}
Nachfrage
s ∈ S; k ∈ K
s
; t = 1, 2, ..., T
Zielfunktion
Min Z =
P
s∈S
Fabriken
P
k∈K
s
Produkte
T
P
t=1
Perioden
l
s
k
· L
s
kt
| {z }
Lagerkosten
+
P
s∈ S
T
P
t=1
u
s
t
· U
s
t
| {z }
Kosten f¨ur
¨
Uberstunden
Produktionsmengenbeschr¨ankung f¨ur die personelle Kapazit¨at
P
k∈K
s
a
s
k
· X
s
kt
| {z }
gesamter
Personalbedarf
− U
s
t
|{z}
¨
Uberstunden
≤ N
s,max
t
| {z }
verf¨ugbare Nor-
malarbeitszeit
s ∈ S; t = 1, 2, ..., T
177
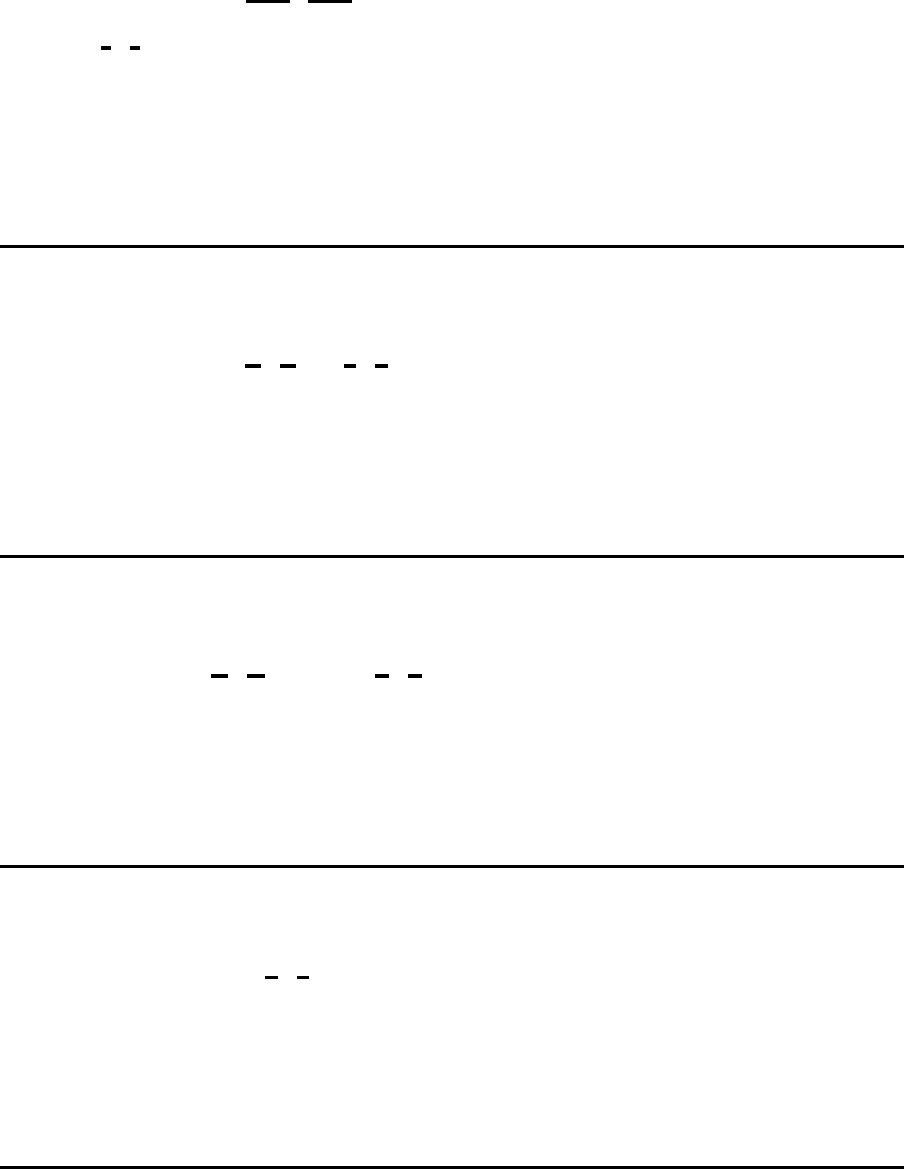
Lagerbilanzgleichung
L
s
k,t−1
| {z }
Anfangsbestand
+ X
s
kt
|{z}
Produktions-
menge
−
Sekund¨ar-
bedarf
z }| {
X
j∈K
Nachfolge-
produkte
q
kj
|{z}
Direktbedarfs
koeffizient
·X
s
jt
− L
s
kt
|{z}
Endbestand
= d
s
kt
|{z}
Nachfrage
s ∈ S; k ∈ K
s
; t = 1, 2, ..., T
Produktionsmengenbeschr¨ankung f¨ur die technische Kapazit¨at
P
k∈K
s
b
s
k
· X
s
kt
| {z }
technischer
Kapazit¨ats-
bedarf
≤ C
s,max
t
| {z }
technische
Kapazit¨at
s ∈ S; t = 1, 2, ..., T
Produktionsmengenbeschr¨ankung f¨ur die personelle Kapazit¨at
P
k∈K
s
a
s
k
· X
s
kt
| {z }
pers oneller
Kapazit¨ats-
bedarf
− U
s
t
|{z}
¨
Uberstunden
≤ N
s,max
t
| {z }
pers onelle
Kapazit¨at
s ∈ S; t = 1, 2, ..., T
Maximale
¨
Uberstunden
U
s
t
≤ U
s,max
t
| {z }
maximale
¨
Uberstunden
s ∈ S; t = 1, 2, ..., T
178
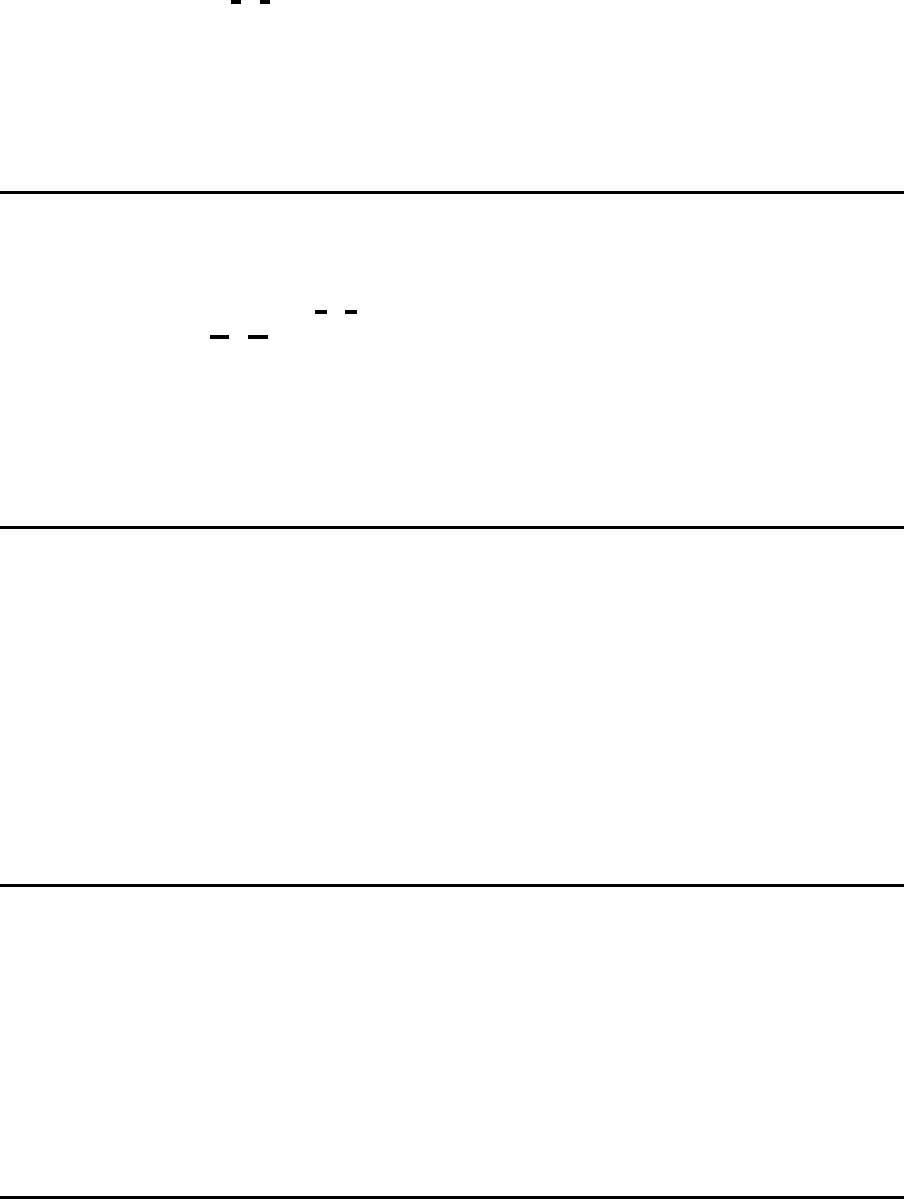
Mindestbestand je Produkt
L
s
kt
≥ L
s,min
kt
|{z }
Mindestbestand
s ∈ S; k ∈ K
s
; t = 1, 2, ..., T
Lagerkapazit¨at
X
k∈K
s
L
s
kt
| {z }
Gesamter
Lagerbestand
≤ L
s,max
t
| {z }
maximaler
Lagerbestand
s ∈ S; t = 1, 2, ..., T
Symbole I
Daten
a
s
k
Produ k tionskoeffizient f¨ur Produktty p k in bezug auf die personelle
Kapazit¨at am S tandort s
b
s
k
Produ k tionskoeffizient f¨ur Produktty p k in bezug auf die technische
Kapazit¨at am S tandort s
C
s,max
t
technische Kapazit¨at in Periode t am Standort s
d
s
kt
Nachfrage f¨ur Produkttyp k in Periode t am Standort s
l
s
k
Lagerkostensatz f¨ur Produkttyp k pro Mengeneinheit und Periode am
Standort s
Symbole II
Daten
N
s,max
t
personelle Kapazit¨at am Standort s in Periode t
U
s,max
t
maximale personelle Zusatzkapazit¨at am Standort s in Periode t
L
s,max
t
maximaler Lagerbestand am Standort s in Period e t
L
s,min
k
Mindestbestand am Standort s f¨ur Produkttyp k
u
s
t
Kosten f¨u r eine Einheit zus¨atzlicher personeller Kapazit¨at am
Standort s
179
Symbole III
Variablen
L
s
kt
Lagerbestand f¨ur Produkttyp k am Standort s am Ende von Periode t
U
s
t
genutzte personelle Zusatzkapazit¨at am Standort s in Periode t
X
s
kt
Produ k tionsm enge von Produkttyp k am Standort s in Periode t
27.3 Beispiel
27.3.1 Version 1
Version 1
Unbesch r¨ankte K apazi t¨at der Fabrik 2
Fabr ik 1
Periode
Technische
Kapazit¨at
Personelle
Kapazit¨at
Maximale
¨
Uberstunden
Nachfrage 1 Nachfrage 2
1 200.0 160.0 100.0 100.0 200.0
2 200.0 160.0 100.0 90.0 190.0
3 200.0 160.0 100.0 110.0 210.0
4 200.0 160.0 100.0 100.0 200.0
Fabr ik 2
Periode
Technische
Kapazit¨at
Personelle
Kapazit¨at
Maximale
¨
Uberstunden
Nachfrage 3
1 400.0 320.0 100.0 0.0
2 400.0 320.0 100.0 0.0
3 400.0 320.0 100.0 0.0
4 400.0 320.0 100.0 0.0
Konstanten – Fabrik 1
Produkt 1
Lagerkostensatz 4.00
Produktionskostensatz 0.00
Personalbedarf pro ME 1.00
Kapazit¨atsbedarf pro ME 0.50
Lager-Anfangsbestand 36.00
Lager-Mindestbestand 0.00
Produkt 2
Lagerkostensatz 4.00
Produktionskostensatz 0.00
Personalbedarf pro ME 0.50
Kapazit¨atsbedarf pro ME 1.00
Lager-Anfangsbestand 220.00
Lager-Mindestbestand 0.00
Sonstiges
Lager-Maximalbestand 99999.00
¨
Uberstundenlohnsatz 5.00
180
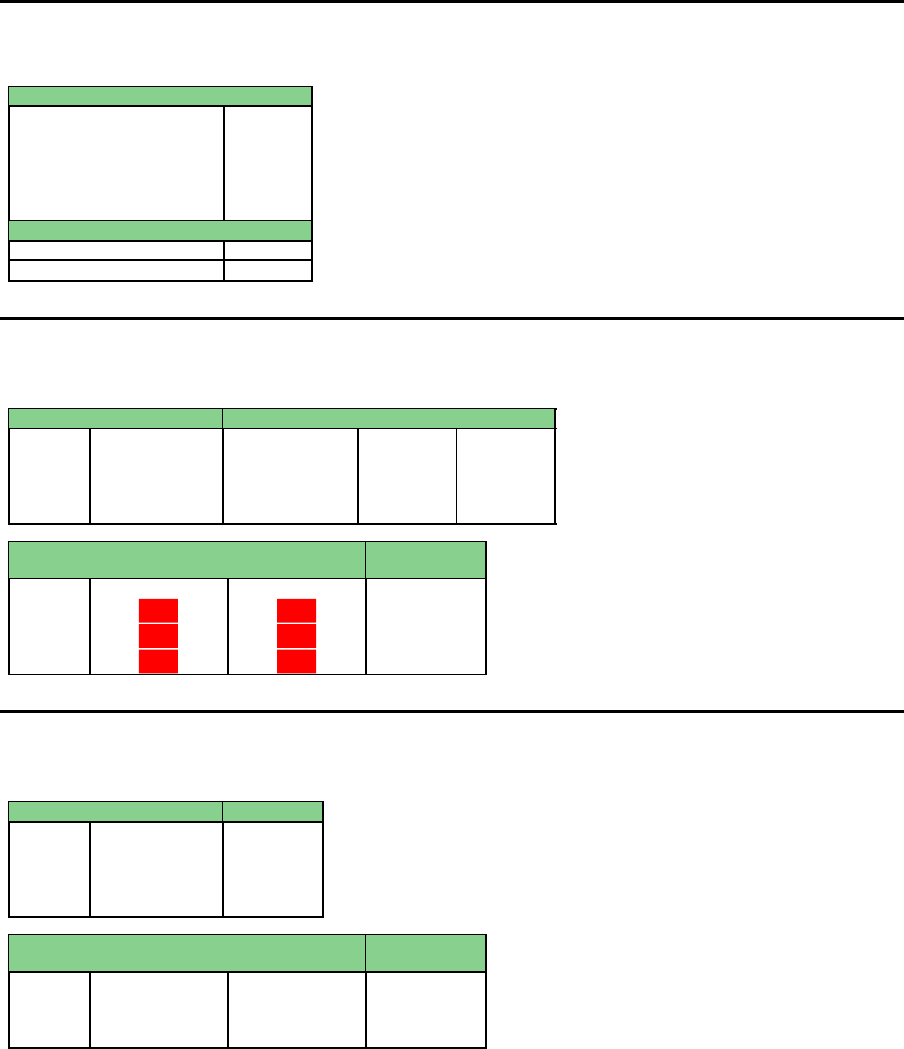
Konstanten – Fabrik 2
Produkt 3
Lagerkostensatz 1.50
Produktionskostensatz 0.00
Personalbedarf pro ME 1.00
Kapazit¨atsbedarf pro ME 1.00
Lager-Anfangsbestand 0.00
Lager-Mindestbestand 0.00
Sonstiges
Lager-Maximalbestand 99999.00
¨
Uberstundenlohnsatz 5.00
L¨osung – Fabrik 1
Periode Prod.-Menge 1 Prod.-Menge 2 Bestand 1 Bestand 2
0 36 220
1 74 125 10 145
2 80 160 - 115
3 110 145 - 50
4 100 150 - -
Periode
Technische
Belastung
Personelle
Belastung
¨
Uberstunden
1 162 136.50 -
2 200 160 -
3 200 160 22.50
4 200 160 15
L¨osung – Fabrik 2
Periode Prod.-Menge 3 Bestand 3
0 -
1 199 -
2 240 -
3 255 -
4 250 -
Periode
Technische
Belastung
Personelle
Belastung
¨
Uberstunden
1 199 199 -
2 240 240 -
3 255 255 -
4 250 250 -
181
27.3.2 Version 2
Version 2
Beschr¨ankte Kapazit¨at der Fa b ri k 2
Fabr ik 1
Periode
Technische
Kapazit¨at
Personelle
Kapazit¨at
Maximale
¨
Ubers tunden
Nachfrage 1 Nachfrage 2
1 200.0 160.0 100.0 100.0 200.0
2 200.0 160.0 100.0 90.0 190.0
3 200.0 160.0 100.0 110.0 210.0
4 200.0 160.0 100.0 100.0 200.0
Fabr ik 2
Periode
Technische
Kapazit¨at
Personelle
Kapazit¨at
Maximale
¨
Ubers tunden
Nachfrage 3
1 250 160 100.0 0.0
2 250 160 100.0 0.0
3 250 160 100.0 0.0
4 250 160 100.0 0.0
Konstanten – Fabrik 1
Produkt 1
Lagerkostensatz 4.00
Produktionskostensatz 0.00
Personalbedarf pro ME 1.00
Kapazit¨atsbedarf pro ME 0.50
Lager-Anfangsbestand 36.00
Lager-Mindestbestand 0.00
Produkt 2
Lagerkostensatz 4.00
Produktionskostensatz 0.00
Personalbedarf pro ME 0.50
Kapazit¨atsbedarf pro ME 1.00
Lager-Anfangsbestand 220.00
Lager-Mindestbestand 0.00
Sonstiges
Lager-Maximalbestand 99999.00
¨
Uberstundenlohnsatz 5.00
Konstanten – Fabrik 2
Produkt 3
Lagerkostensatz 1.50
Produktionskostensatz 0.00
Personalbedarf pro ME 1.00
Kapazit¨atsbedarf pro ME 1.00
Lager-Anfangsbestand 0.00
Lager-Mindestbestand 0.00
Sonstiges
Lager-Maximalbestand 99999.00
¨
Uberstundenlohnsatz 5.00
182
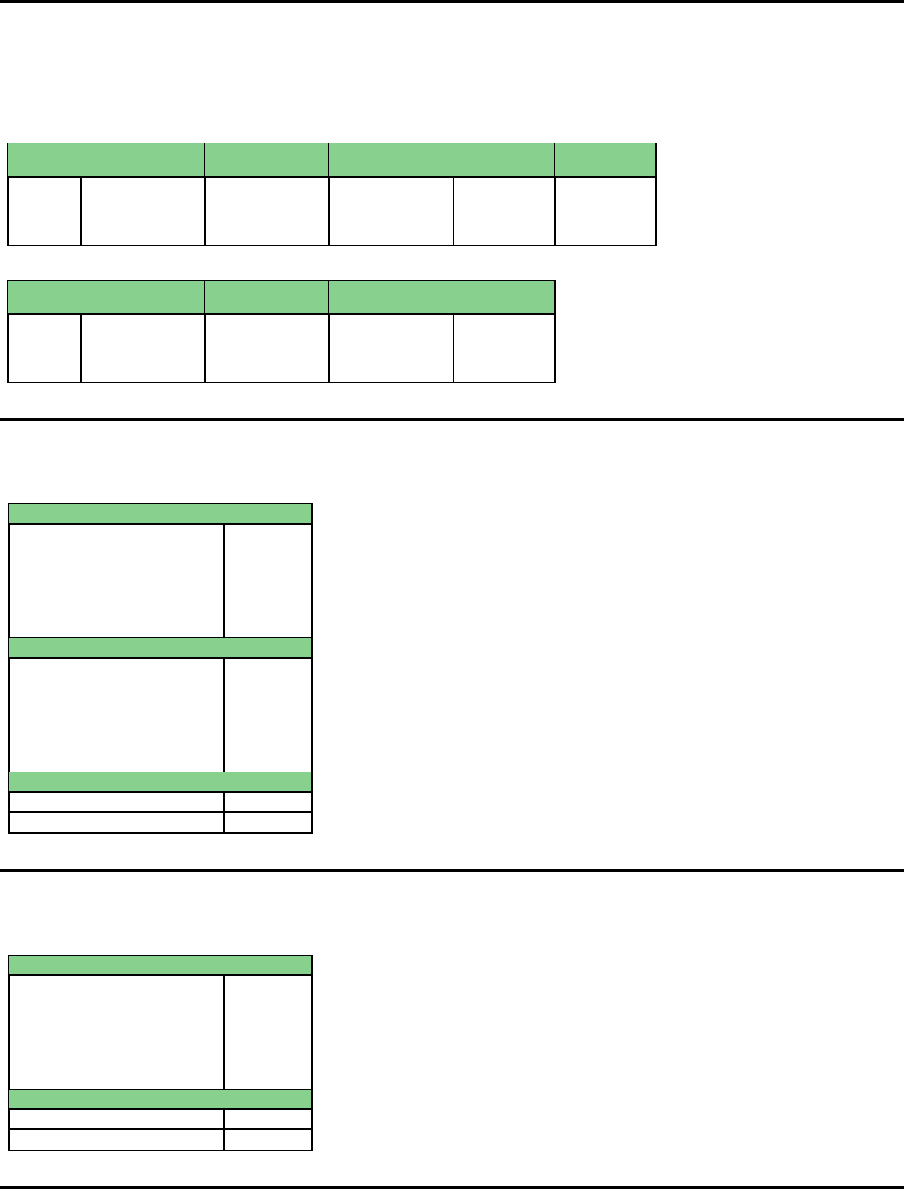
L¨osung – Fabrik 1
Periode Prod.-Menge 1 Prod.-Menge 2 Bestand 1 Bestand 2
0 36 220
1 84 120 20 140
2 80 160 10 110
3 100 150 - 50
4 100 150 - -
Periode
Technische
Belastung
Personelle
Belastung
¨
Uberstunden
1 162 144 -
2 200 160 -
3 200 160 15
4 200 160 15
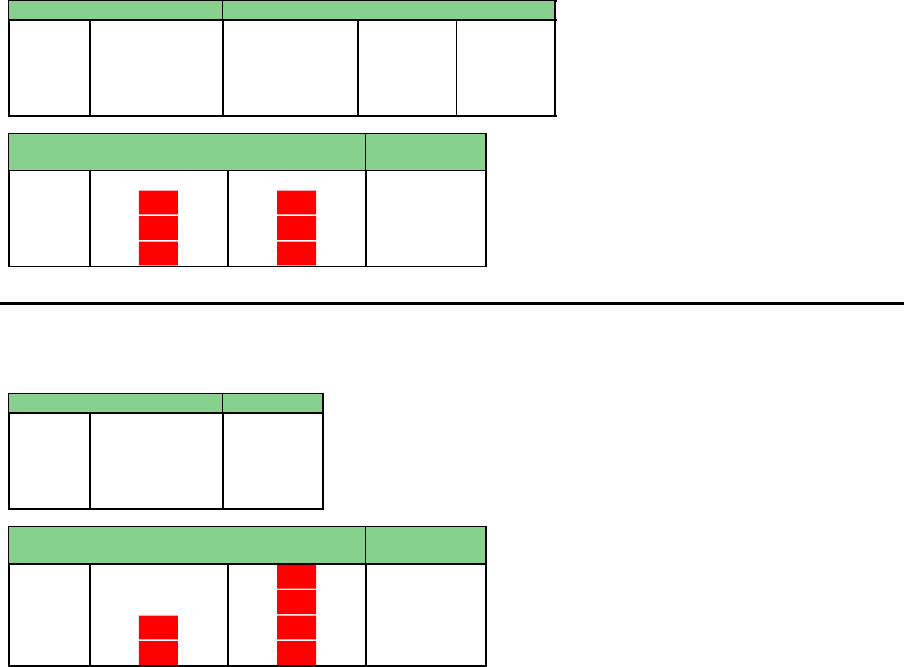
L¨osung – Fabrik 2
Periode Prod.-Menge 3 Bestand 3
0 -
1 204 -
2 240 -
3 250 -
4 250 -
Periode
Technische
Belastung
Personelle
Belastung
¨
Uberstunden
1 204 160 44
2 240 160 80
3 250 160 90
4 250 160 90
183
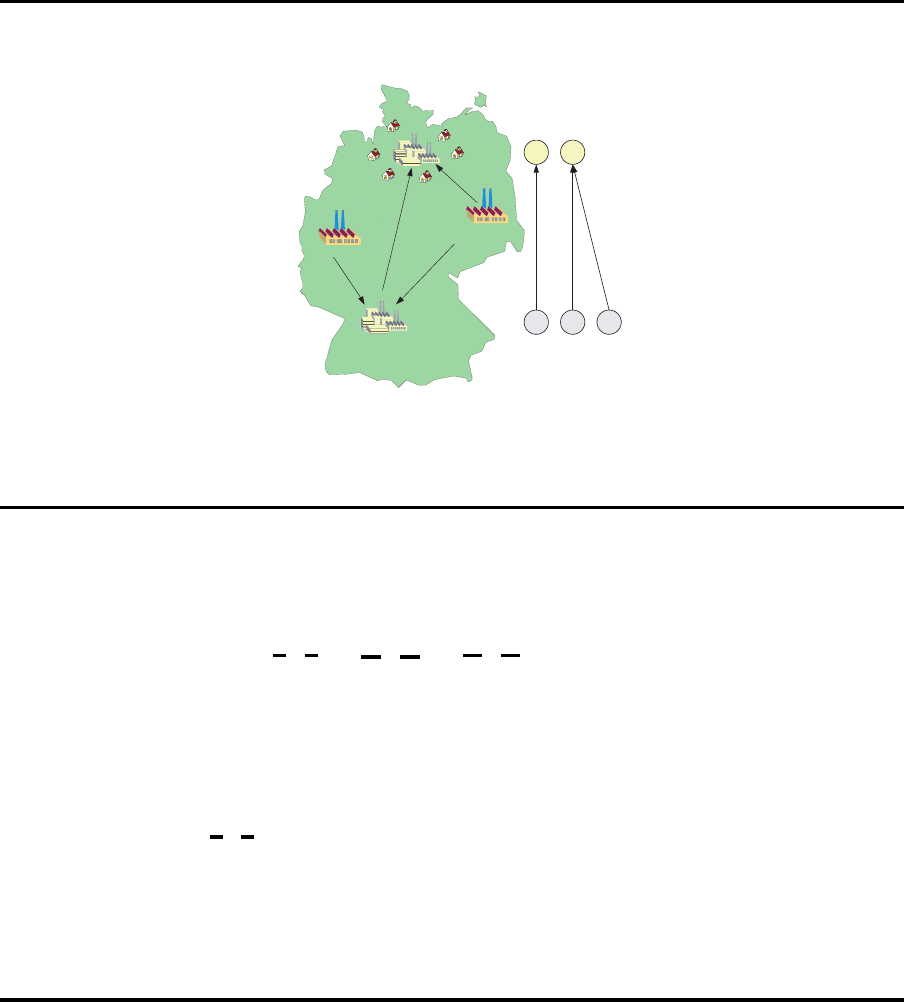
28 Modell 6 – Lieferanten
28.1 Annahmen
Mehrere Fabriken, Lieferanten
Vorprodukte
(Fabrik 2)
Endprodukte
(Fabrik 1)
1 2
a b c
Erzeugnisstruktur
Lieferanten
Vorprodukte
Endprodukte
Lieferanten
Vorprodukte
28.2 Modellformulierung
Zielfunktion
Min Z =
P
s∈S
P
k∈K
s
T
P
t=1
l
s
k
· L
s
kt
| {z }
Lagerkosten
+ c
p
sk
· X
s
kt
| {z }
Produktions-
kosten
+ c
b
sk
· B
s
kt
| {z }
Beschaffungs
kosten
+
P
s∈S
T
P
t=1
u
s
t
· U
s
t
| {z }
Kosten f¨ur
¨
Uber-stunden
Lagerbilanzgleichung
184

L
s
k,t−1
| {z }
Anfangsbestand
+ X
s
kt
|{z}
Produktions-
menge
+ B
s
kt
|{z}
Beschaffungs-
menge
−
X
j∈K
q
kj
· X
s
jt
| {z }
Sekund¨ar-
bedarfsmenge
− L
s
kt
|{z}
Endbestand
= d
s
kt
|{z}
Nachfrage-
menge
s ∈ S; k ∈ K
s
; t = 1, 2, ..., T
Produktionsmengenbeschr¨ankung f¨ur die technische Kapazit¨at
P
k∈K
s
b
s
k
· X
s
kt
| {z }
technischer
Kapazit¨ats-
bedarf
≤ C
s,max
t
| {z }
technische
Kapazit¨at
s ∈ S; t = 1, 2, ..., T
Produktionsmengenbeschr¨ankung f¨ur die personelle Kapazit¨at
P
k∈K
s
a
s
k
· X
s
kt
| {z }
gesamter
Personalbedarf
− U
s
t
|{z}
¨
Uberstunden
≤ N
s,max
t
| {z }
verf¨ugbare Nor-
malarbeitszeit
s ∈ S; t = 1, 2, ..., T
Produktionsmengenbeschr¨ankung f¨ur die personelle Kapazit¨at:
P
k∈K
s
a
s
k
· X
s
kt
| {z }
pers oneller
Kapazit¨ats-
bedarf
− U
s
t
|{z}
¨
Uberstunden
≤ N
s,max
t
| {z }
pers onelle
Kapazit¨at
s ∈ S; t = 1, 2, ..., T
maximale
¨
Uberstunden:
185

U
s
t
≤ U
s,max
t
| {z }
maximale
¨
Uberstunden
s ∈ S; t = 1, 2, ..., T
Mindestbestand je Produkt
L
s
kt
≥ L
s,min
kt
|{z }
Mindestbestand
s ∈ S; k ∈ K
s
; t = 1, 2, ..., T
Lagerkapazit¨at
X
k∈K
s
L
s
kt
| {z }
gesamter
Lagerbestand
≤ L
s,max
t
| {z }
maximaler
Lagerbestand
s ∈ S; t = 1, 2, ..., T
186
Teil XII
Kapazitierte
Hauptproduk ti onsprogrammpla nung
29 Einf¨uhrung
Literaturhinweis
G¨unther and Tempelmeier (2016), Teil D, Einleitung
G¨unther and Tempelmeier (2016), Kapitel 8.3
Stichworte Struktur der Produktionsplanung und -steuerung; Besch¨aftigungsgl¨at t ung ; Haupt-
produktionsprogrammplanung; Kapazit¨aten; Nachfrageprognosen; Belastungs-
faktoren; Kapazit¨atsbelastungsprofil; mehrstufige Produktion; Produktaggr e-
gation; Vorlaufzeiten
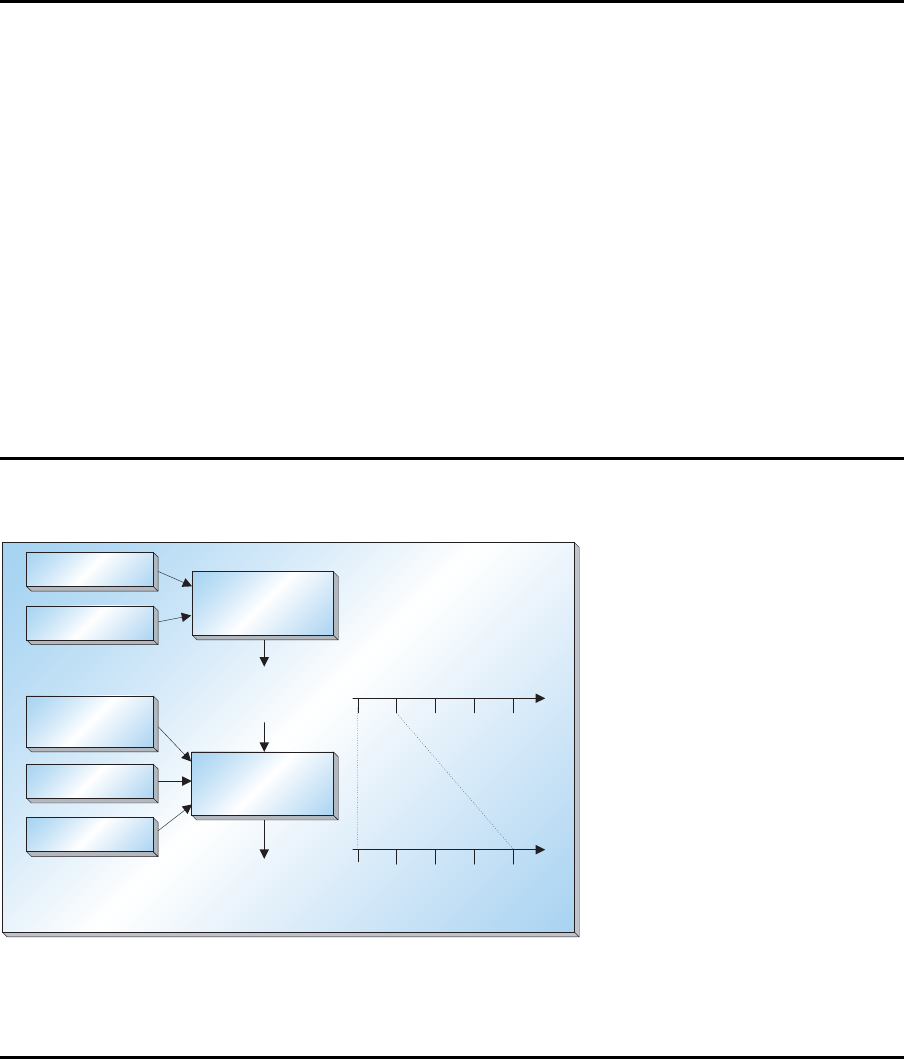
Besch¨aftigungsgl¨attung – Hauptproduktionsprogrammplanung
Nachfrageprognosen;
Kundenaufträge
Kapazitäten
Lagerbestände
kurzfristiges
Hauptproduktions-
programm für
Endprodukte
Hauptproduktions-
programmplanung
aggregierte
Nachfrageprognosen
Beschäftigungs-
glättung
aggregierte
Kapazitäten
Hauptproduktions-
programmplanung
mittelfristiger
Produktionsplan
für Produkttypen
detaillierte
Nachfrageprognosen;
Kundenaufträge
detaillierte
Kapazitäten
Monate
Wochen
aktuelle
Lagerbestände
29.1 Beispiel
187
Beispiel
Periode (4 Wochen) 0 1 2 3
prognostizierte Nachfragemenge - 1200 1100 800
Produktionsmenge - 1000 1000 1000
Lagerbestand (Periodenende) 800 600 500 700
Produktspezifische Nachfrageprognosen
Monat 1
Woche 1 2 3 4
Produkt 1 100 100 100 100
Produkt 2 150 125 125 100
Produkt 3 75 75 75 75
Summe Woche 325 300 300 275
Summe Monat 1200
Monat 2
Woche 5 6 7 8
Produkt 1 100 80 75 75
Produkt 2 75 75 75 65
Produkt 3 100 120 125 135
Summe Woche 275 275 275 275
Summe Monat 1100
Monat 3
Woche 9 10 11 12
Produkt 1 75 75 65 50
Produkt 2 65 65 60 50
Produkt 3 135 60 50 50
Summe Woche 275 200 175 150
Summe Monat 800
Produktionsplan
Monat 1
Woche 0 1 2 3 4
Produkt 1 Prod.- Menge - - 250 -
Produkt 2 Prod.- Menge - 250 - 250
Produkt 3 Prod.- Menge 250 - - -
P
Produktionsmengen 250 250 250 250
Kapazit¨atszuweisung 250 250 250 250
Abweichung 0 0 0 0
Monat 2
Woche 4 5 6 7 8
Produkt 1 Prod.- Menge - - 125 - 125
Produkt 2 Prod.- Menge 250 - 125 - 125
Produkt 3 Prod.- Menge - 250 - 250 -
P
Produktionsmengen 250 250 250 250
Kapazit¨atszuweisung 250 250 250 250 250
Abweichung 0 0 0 0 0
Monat 3
Woche 8 9 10 11 12
Produkt 1 Prod.- Menge 125 - 250 - -
Produkt 2 Prod.- Menge 125 - - 250 -
Produkt 3 Prod.- Menge - 250 - - 250
P
Produktionsmengen 250 250 250 250 250
Kapazit¨atszuweisung 250 250 250 250 250
Abweichung 0 0 0 0 0
188

Lagerbest¨ande
Monat 0 1
Woche 0 1 2 3 4
Produkt 1 400 300 200 350 250
Produkt 2 250 100 225 100 250
Produkt 3 150 325 250 175 100
800 725 675 625 600
Lagerbestand (aggregiert) 800 - - - 600
innerperiodige Abweichung 0 125 75 25 0
Monat 2
Woche 4 5 6 7 8
Produkt 1 250 150 195 120 170
Produkt 2 250 175 225 150 210
Produkt 3 100 250 130 225 120
600 575 550 525 500
Lagerbestand (aggregiert) 600 - - - 500
innerperiodige Abweichung 0 75 50 25 0
Monat 3
Woche 8 9 10 11 12
Produkt 1 170 95 270 205 155
Produkt 2 210 145 80 270 220
Produkt 3 120 235 175 125 325
500 475 525 600 700
Lagerbestand (aggregiert) 500 - - - 700
innerperiodige Abweichung 0 (225) (175) (100) 0
29.2 Globale Belastungsfaktoren
RCCC, RCCP
• Rough-cut capacity check
• auch: Rough-cut capacity check
• keine Planungsfunktion, lediglich Zul¨assigkeit spr¨ufung
RCCC – Globale Belastungsfaktoren
Produktionsplan
P
(K × X)
=
100 80 120 100 120 60
40 0 60 0 40 0
RCCC – Globale Belastungsfaktoren
Faktoren
F
(J × K)
=
0.4 1.6
0.6 2.4
2.0 2.0
189
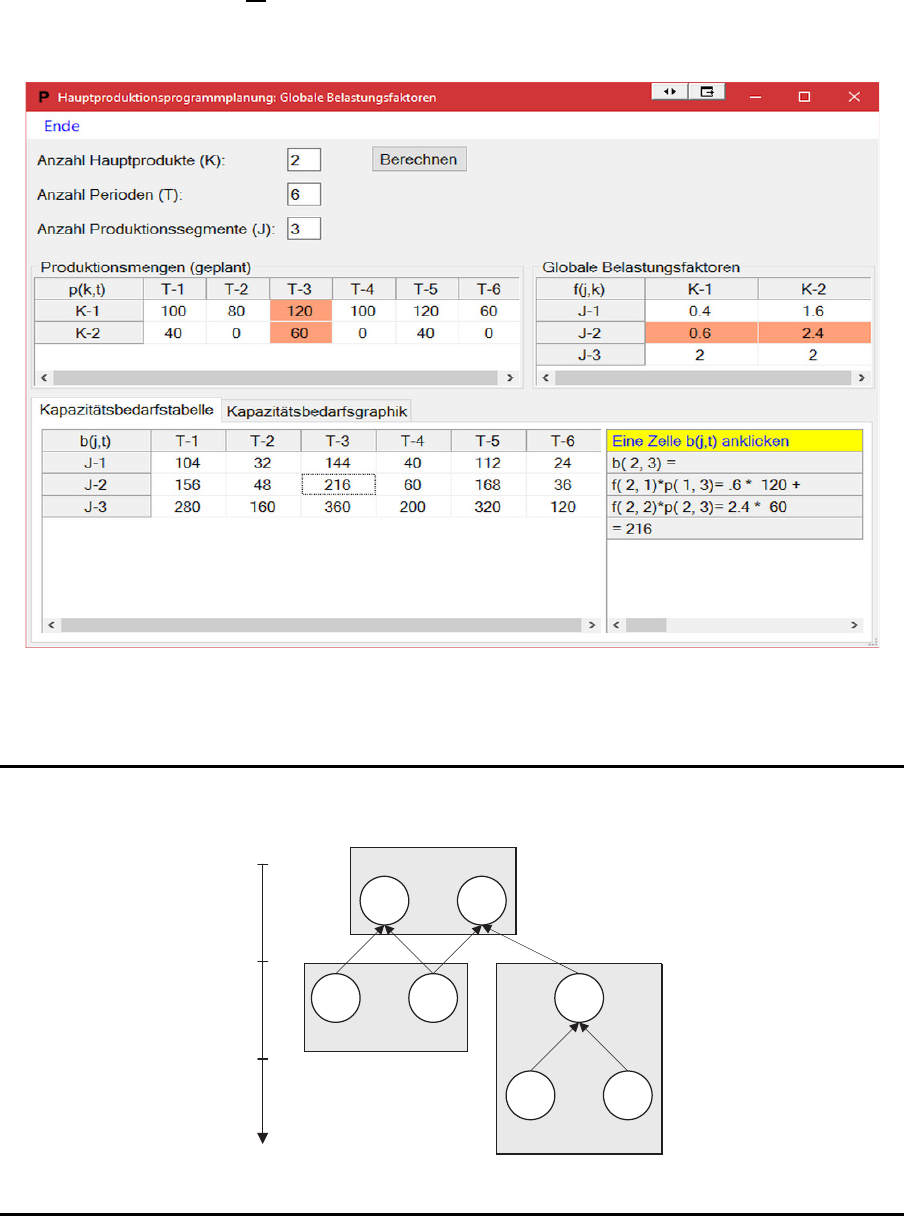
RCCC – Globale Belastungsfaktoren
Belastungen
B
(J × T )
=
104 32 144 40 112 24
156 48 216 60 168 36
280 160 360 200 320 120
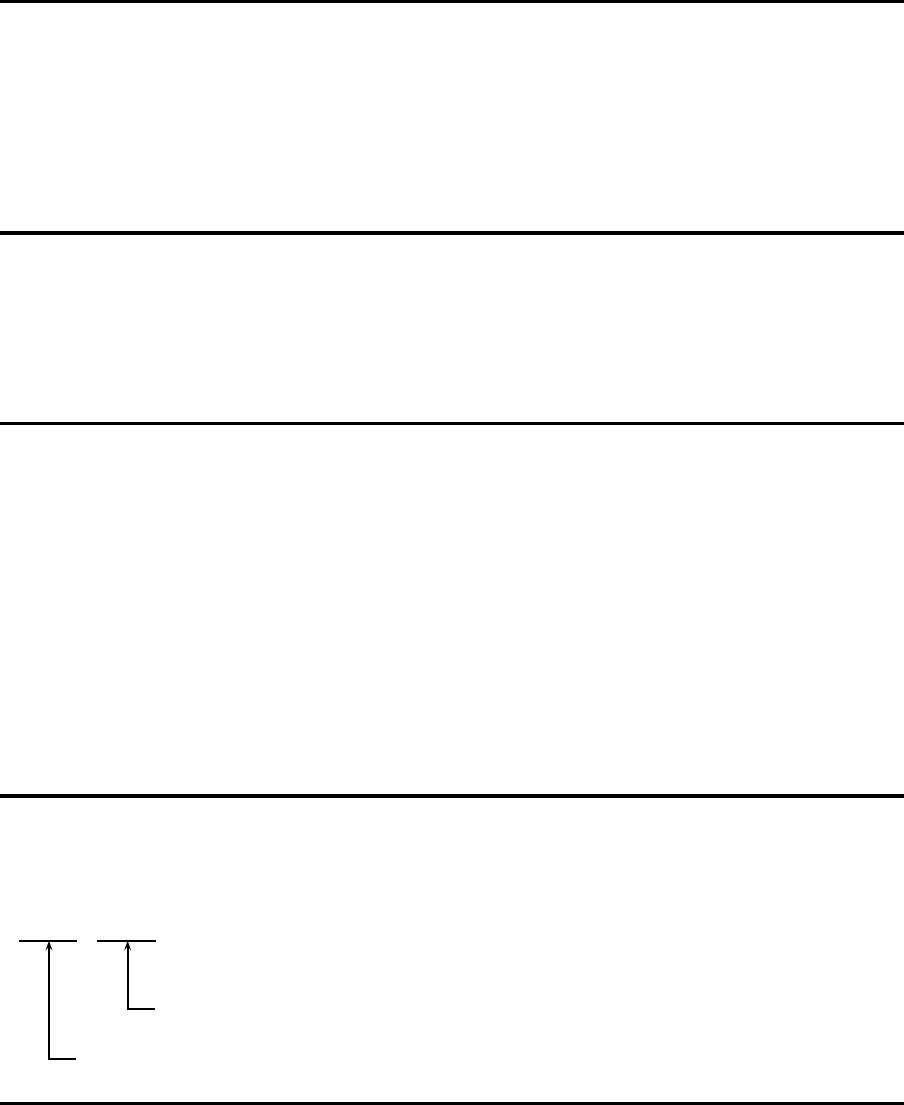
29.3 Kapazit¨atsbelastungsprofil
Erzeugnisstrukturen/Produktionssegmente
Produktionssegment 3
Produktionssegment 2
Produktionssegment 1
A/1
C/1 E/4D/3
F/2
B/2
G/1
0
1
2
Vorlaufzeit
(Perioden)
111 1
11
190

RCCC – Kapazit¨atsbelastungsprofil
Vorlaufperiode 2 1 0
Endprodukt A
Produktionssegment 1 – – 1
Produktionssegment 2 – 4 –
Produktionssegment 3 – – –
Endprodukt B
Produktionssegment 1 – – 2
Produktionssegment 2 – 3 –
Produktionssegment 3 3 4 –
191
30 LP-Modell zur Hauptproduktionsplanung
30.1 Modellformulierung
Literaturhinweis
G¨unther and Tempelmeier (2016), Modell HPP
Zielfunktion
Minimiere Z =
K
X
k=1
T
X
t=1
h
k
· y
kt
+
T
X
t=1
J
X
j=1
u
t
· U
jt
u. B. d. R.
x
kt
+ y
k,t−1
− y
kt
= d
kt
k = 1, 2, . . . , K; t = 1, 2, . . . , T
K
X
k=1
Z
k
X
z=0
f
jkz
·x
k, t+z
− U
jt
≤ b
jt
j = 1, 2, ..., J; t = 1, 2 , ..., T
30.2 Beispiel
Siehe Erzeugnisstruktur aus Abschnitt 29.3.
Beispiel – P rodukte A und B
1 · x
At
Kapazit¨atsbedarf f¨ur das Endpr odukt A
+ 2 ·x
Bt
Kapazit¨atsbedarf f¨ur das Endpr odukt B
− U
1t
≤ b
1t
t = 1, 2, ..., T
192

Beispiel – P rodukte C und D
4 · x
A, t+1
Kapazit¨atsbelastung verursacht durch Vorprodukte
C und D (zugerechnet der Produktion
von Endprod ukt A in der Periode t + 1)
+ 3 · x
B, t+1
Kapazit¨atsbelastung verursacht durch
Vorprodukt D zugerechnet der Produktion
von Endprodukt B in der Periode t + 1)
−U
2t
≤ b
2t
Beispiel – P rodukte E, F und G
4 · x
B, t+1
Kapazit¨atsbelastung verursacht durch
Vorprodukt E (zugerech net der
Produ k tion von End produkt B
in der Per iode t + 1)
+ 3 · x
B, t+2
Kapazit¨atsbelastung verursacht durch
Vorprodukte F und G (zugerechnet
der Produktion von Endpr odukt B in der
Periode t + 2)
− U
3t
≤ b
3t
Nachfragemengen
Periode
1 2 3 4 5 6 7 8
Endprodukt A – 45 30 10 30 50 10 20
B – – 25 30 25 30 20 10
Produktionsmengen
Periode
1 2 3 4 5 6 7 8
Endprodukt A – 47.50 27.50 31.25 31.25 27.5 10.0 20.0
B – – 30.0 25.0 25.0 30.0 20.0 10.0
193
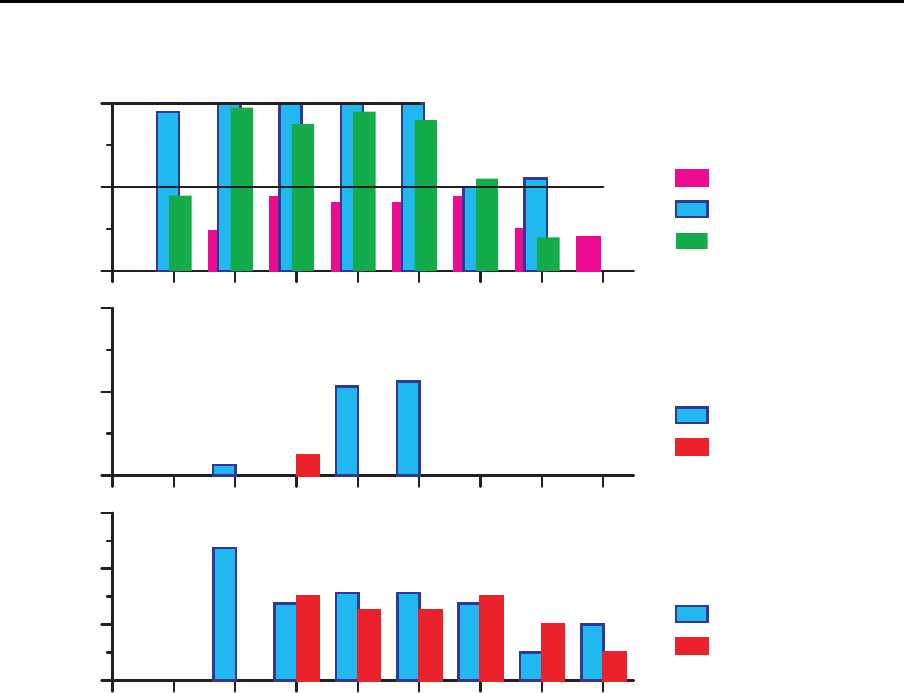
Ergebnis
0
20
40
60
Produktionsmenge
0
20
40
Lagerbestand
0
100
200
Belastung
0 1 2 3 4 5 6 7 8
Periode
Lager A
Lager B
Produktion A
Produktion B
Belastung 1
Belastung 2
Belastung 3
194