
1
Teil IX
Operative Produktionsplanung und
-steuerung
20 Planungssituation
Gegeben ...
Daten
• Produktions- und Marktstrategien
• Standorte
• Infrastruktur (Produktionssegmente, L¨ager, Materialflußsysteme, etc.)
Literaturhinweis
G¨unther and Tempelmeier (2016), Teil D, Einleitung
Stichworte Struktur der Produktionsplanung und -steuerung; Master Planning; Kapazit¨aten;
Nachfra geprognosen
Supply Chain Optimierung
Planungsstruktur
Deterministische Sicht
Bau-
stellen-
produktion
Werkstatt-
produktion
Zentren-
produktion
Fließ-
produktion
JIT-
Produktion
...
Produktionssegmente (Standort 1)
Kapazitätsorientierte Planung (Standort 1)
Bau-
stellen-
produktion
Werkstatt-
produktion
Zentren-
produktion
Fließ-
produktion
JIT-
Produktion
...
Produktionssegmente (Standort N)
Kapazitä
tsorientierte Planung (
Standort N
)
...
Lieferungen Lieferungen Kunden
Standortü
bergreifende Produktions- Beschaffungs- und Transportplanung
(Supply Network Planning, Master Planning, Enterprise Planning)
aggregiert
detailliert
Distribution
Lieferanten
Beschaffung
Stochastische Sicht
Puffe
fferungsmechanismen, Sicherheitsbest
ä
nde, Sicherheitszeiten
Unterstützende Module:
Nachfrageprognose, Verf
ü
gbarkeitspr
ü
onitor
fung (Available-to-promise), Warn-Mon
Supply Network
148

Festzulegen ...
• Nachfra gemengen und Produktionsmengen
• absatzf¨ahige Produkte
• Vo rprodukte
• Produktionsprozesse
Zwei Planungsebenen
• Besch¨aftigungsgl¨attung
• kapazitierte Hauptpro duktionsprogrammplanung
Prognosen
• Aggregierte mehrperiodige Nachfra geprognosen
• Detaillierte kurzfristige Progno sen
149

Teil X
Aggregierte Gesa mtplanung –
Einstufige Probleme
Literaturhinweis
G¨unther and Tempelmeier (2016), Kapitel 8
Tempelmeier ( 2018), Teil B, Abschnitt 1
Tempelmeier ( 2017), Kapitel B.1
Stichworte Planungsebenen; Beziehungen zwischen den Planungsebenen; Advanced Plan-
ning Systems;
¨
Uberstunden; Kurzarbeit; Fremdbezug; Vorratsproduktion; Syn-
chronisation (chase); Emanzipation (level); Supply Network Planning
21 Einstufi ge Probleme – Einf¨uhrung
21.1 Einf¨uhrung
Aggregierte Gesamtplanung
•
¨
Uberstunden bzw. Kurzarbeit
• Fremdbezug bei externen Lieferant en
• saisonbedingte So nder- und Freischichtenregelungen
• Urlaubsplanung
• Verteilung von Produktionsmengen auf verschiedene Produktionsstandorte
21.2 Nachfrageentwick lung und Pro duktion
Synchronisation
150
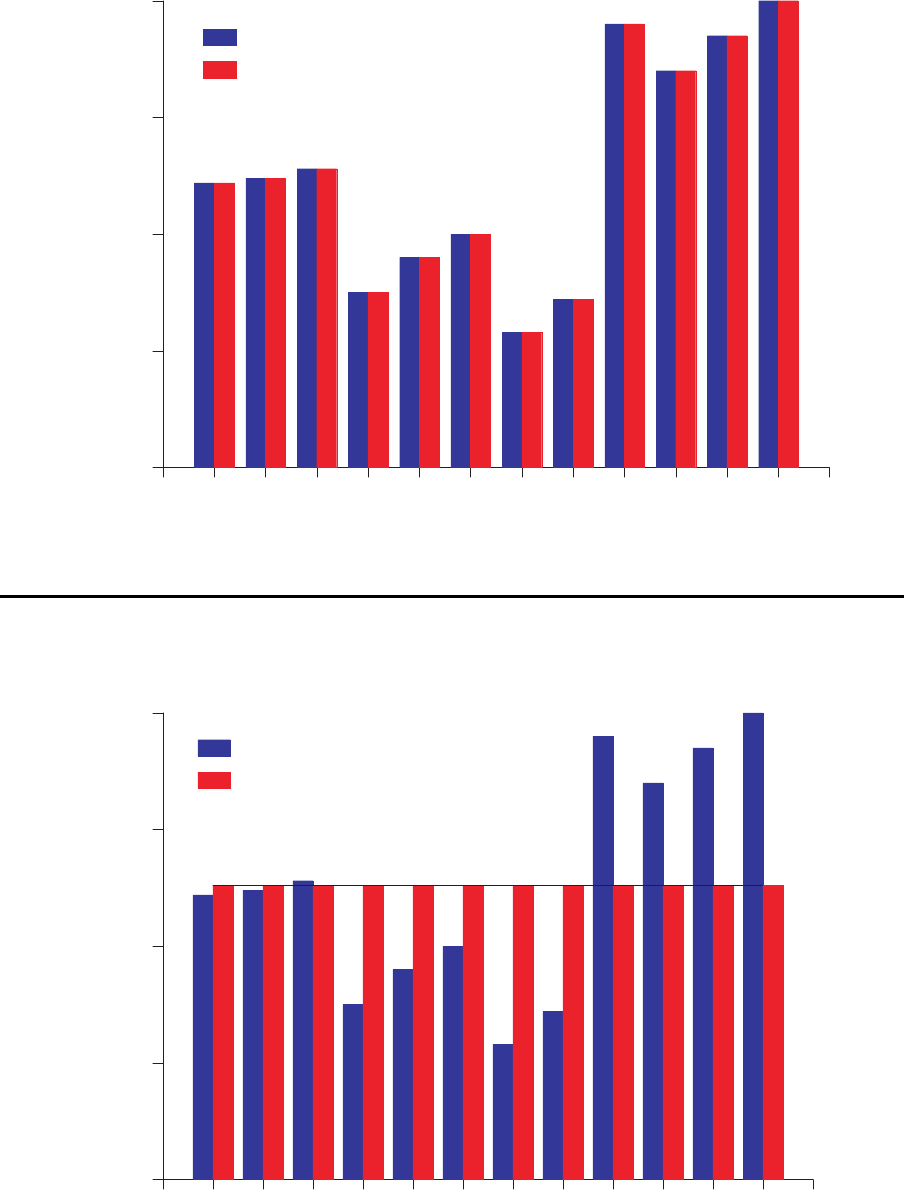
0
50
100
150
200
(in Tausend Stück)
Nachfrage- bzw. Produktionsmenge
Jan Feb Mar Apr Mai Jun Jul Aug Sep Okt Nov Dez
Nachfragemenge
Produktionsmenge
Emanzipation
0
50
100
150
200
(in Tausend Stück)
Nachfrage- bzw. Produktionsmenge
Jan Feb Mar Apr Mai Jun Jul Aug Sep Okt Nov Dez
Nachfragemenge
Produktionsmenge
151
21.3 Problem
Entscheidungsvariablen der Besch¨aftigungsgl¨attung
• Prim¨are Variablen
– Produktionsmengen
– Transportmengen
– Beschaff ung smengen
• Sekund¨are Variablen
– Kurzfristige Stillegung von Betriebseinheiten
– Ver¨anderung der Arbeitszeit
– Ver¨anderung der Arbeitsgeschwindigkeit
– Fremdvergabe von Auftr¨ag en
– Lohnfertigung
Weitere Variablen
• Lagerbest¨ande
• Fehlmengen
Komponenten der Zielfunktion
• Va riable Produktionskosten
• Va riable Bescha ff ung skosten
• Transportkosten
• Produktionsniveau¨anderungsko sten
• Lagerko sten (Kapitalbindung)
• Lagerko sten (Lagerbetrieb)
• (Fehlmengenkosten)
152
Problem
¨
Ubersicht
Beschäftigungs-
glättung
Ziel:
Minimiere Kosten
oder
Glätte Beschäftigung
Entscheidungen:
Abstimmung von
Produktions- und
Nachfragemengen
Produktionsmengen
Personalbestand
Lagerbestände
Transportmengen
Nachfrageprognosen
Startbedingungen
zulässige Optionen
Kostenparameter
Fremdbeschaffungsmengen
21.4 Praxisbeispiel
Betrachten wir eine einfaches Beispiel (entnommen aus Peterson/Silver(1979)) und eine
sehr einfache heuristische L¨osungsmethode, wie sie oft in der Pra xis eingesetzt wird.
In der folgenden Tabelle sind die prognostizierten Nachfrag emengen f¨ur eine Produkt-
gruppe bezogen auf sechs zweimonatige Perioden angegeben.
Ein Beispiel
Periode prognostizierte Nachfragemenge
t absolut kumuliert
1 30 30
2 30 60
3 120 180
4 90 270
5 60 330
6 30 360
Das folgenden Bild zeigt verschiedene manuell erstellte Produktionspl¨ane.
153
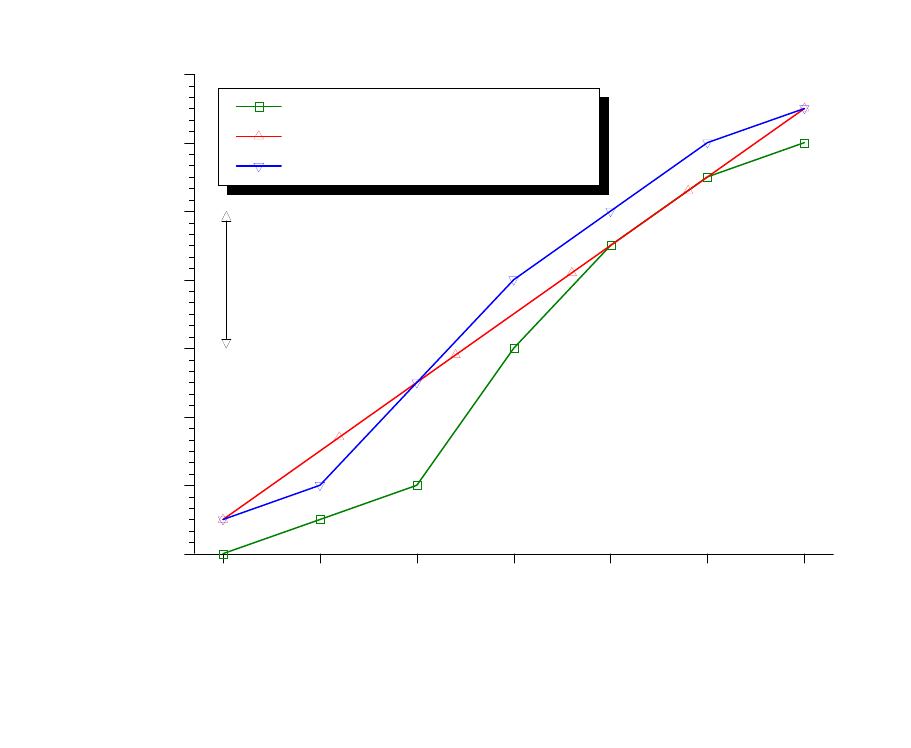
Beispiel - Mehrere Pl¨ane
0
60
120
180
240
300
360
420
Kumulierte Produktionsstunden
0 1 2 3 4 5 6
Ende der Periode
(2 Monate)
g
f
a
b
c
d
e
kumulierte Nachfragemengen
konstante Produktionsmengen
variable Produktionsmengen
max. Lagerbestand
Die Linie a-e markiert die kumulierte Produktionsmenge (ausgedr¨uckt in Stunden), wie
sie sich aufgrund eines Produktionsplanes mit gleichbleibenden Produktionsmengen und
damit gleichm¨aßiger Auslastung ergibt (E manzipation). Dieser Produktionsplan sieht
in jeder Teilperiode eine gleichm¨aßige Produktionsmenge von 30 Stunden pro Monat (60
Std pro Periode) vor . Bei dieser Produktionsmenge ist sichergestellt, daß die Nachfrage-
menge zu jedem Zeitpunkt voll (d. h. ohne Fehlmengen) erf¨ullt wird. Dies kann man an
der Linie der kumulierten Produktionsmengen a blesen, die zu jedem Zeitpunkt ¨uber der
Linie der kumulierten Nachfragemengen liegt. Dieser Produktionsplan ist dann
zul¨assig, wenn die erwartete kumulierte Nachfragemenge eintritt. In der Abbildung wird
angenommen, daß zum Planungszeitpunkt 0 der Lagerbestand eine Monatsproduktion
(d. h. 30 Std.) betr¨agt.
Der vertikale Abstand zwischen der Linie der kumulierten Produktionsmenge und der
Linie der kumulierten Nachfragemenge ist der Lagerbest and bzw. die Fehlmenge. Jeder
Produktionsplan, dessen Linie der kumulierten Produktionsmengen in jeder Periode die
Linie der kumulierten Nachfragemengen nicht unterschreitet, und der in einem Punkt
¨uber dem Punkt f endet, ist ein zul¨assiger Produktionsplan, in dem evtl. auch ein
Lagerbestand am Ende der Planungsperiode vor gesehen sein kann.
In diesem Beispiel ist noch eine Nebenbedingung bez¨uglich der maximalen Lagerbe-
standsmenge zu beachten. Sie ergibt sich aus der Kapazit¨at des Lagers. Der Lagerbe-
stand darf – ausgedr¨uckt in Produktionsstunden – 120 nicht ¨uberschreiten. Dies wird
durch die senkrechte Linie dargestellt. Vergleicht man die vertikale Differenz zwischen
kumulierter Produktionsmenge und kumulierter Nachfragemenge, dann kann man die
154
Zul¨assigkeit eines Produktionsplans einfach feststellen.
Man kann f¨ur das vorliegende Beispiel nun eine ganze Anzahl von verschiedenen zul¨assi-
gen Produktionspl¨anen erzeugen.
So kann man zuerst einen Produktionsplan mit einer konstanten Produktionsleistung
pro Periode erzeugen und dann einen, der etwas mehr a n den Verlauf der kumulierten
Nachfra gemenge angepaßt ist. Zur Auswahl des optima len Produktionsplans m¨ussen die
einzelnen Alternat iven bewertet werden.
Die folg ende Tabelle zeigt den Produktionsplans a-b-c-d-e und die Berechnung der damit
verbundenen Kosten. Dabei sind wir (in Anlehnung an die amerikanische Vorlage) davon
ausgegangen, daß die Produktionsmenge nur durch eine Ver¨anderung des Per-
sonalbest ands (d. h. Erh¨ohung der m¨oglichen No rmalarbeitsstunden) beeinflußt wird.
¨
Uberstunden werden somit nicht als Option ber¨ucksicht igt.
Bewertung des Produktionsplans (Linie a-b-c-d-e)
Personalb estand Produktionsmenge
t Anfang Ende
Einstel-
lungen
Entlas-
sungen
Normal-
arbei t
¨
Uber-
stunden
Nach-
frage
Lager-
bestand
0 30 30
1 30 30 0 0 30 0 30 30
2 30 90 60 0 90 0 30 90
3 90 90 0 0 90 0 120 60
4 90 60 0 30 60 0 90 30
5 60 60 0 0 60 0 60 30
6 60 30 0 30 30 0 30 30
Summen: 360 60 60 360 0 360 270
Kosten pro
Einheit:
0 120 70 200 300 0 40
Kosten: 0 7200 4200 72000 0 0 10800
Summe: 94200
Die Lohnkosten werden als zeitabh¨angige L¨ohne als Funktion des geleisteten Nor -
malarbeitstunden und evtl. der geleisteten
¨
Uberstunden berechnet. Mit dieser einfachen
graphischen Methode findet man zwar einen zul¨assigen Produktionsplan (f¨ur mehrere
Perioden) – allerdings nur im Einproduktfall. Man weiß aber nicht, wie weit dieser Pro-
duktionsplan vom Optimum entfernt ist.
155
Im folgenden werden verschiedene Planungssituationen aus dem Bereich Master Plan-
ning (Supply Network Planning, Besch¨aftigungsgl¨attung) vorgestellt, die mit Modellen
der linearen Optimierung bearbeitet werden k¨onnen. Diese Modelle sind (in erweiterte
Form) in einigen der in der Praxis angebotenen Softwaresysteme zum Advanced Plan-
ning implementiert.
Zun¨achst werden einstufige Probleme betrachtet. Ausgehend von einer gegebenen
Nachfra geprognose geht es zun¨achst nur um Entscheidungen ¨uber die Zuordnung von
Produktionsmengen auf m¨oglicherweise mehrere vorhandene Produktionsstandorte und
evtl. auch um die Frage, ob anstelle der Eigenproduktion in einzelnen Perioden bei einem
Lieferanten beschafft werden soll.
Sp¨ater wird die Modellierung auf echte mehrstufige Wertsch¨o pf ung sketten ausgedehnt.
Dann werden mehrere Produktionsst¨atten betrachtet, wobei eine Gruppe der Produk-
tionsst¨at t en die Vorpr odukte und die andere Gruppe die Endprodukte produziert. Bei
der Entscheidung ¨uber die periodenbezogenen Produktionsmengen in einem Standort, der
Endprodukte produziert, muß dann ber¨ucksichtigt werden, daß rechtzeitig ausreichende
Mengen der ben¨otigten Vorprodukte bereitstehen, die in anderen Standorten produziert
werden.
Die Beispielrechnungen wurden in den meisten F¨allen mit dem Produktions-Management-
Trainer ausgef¨uhrt.
156
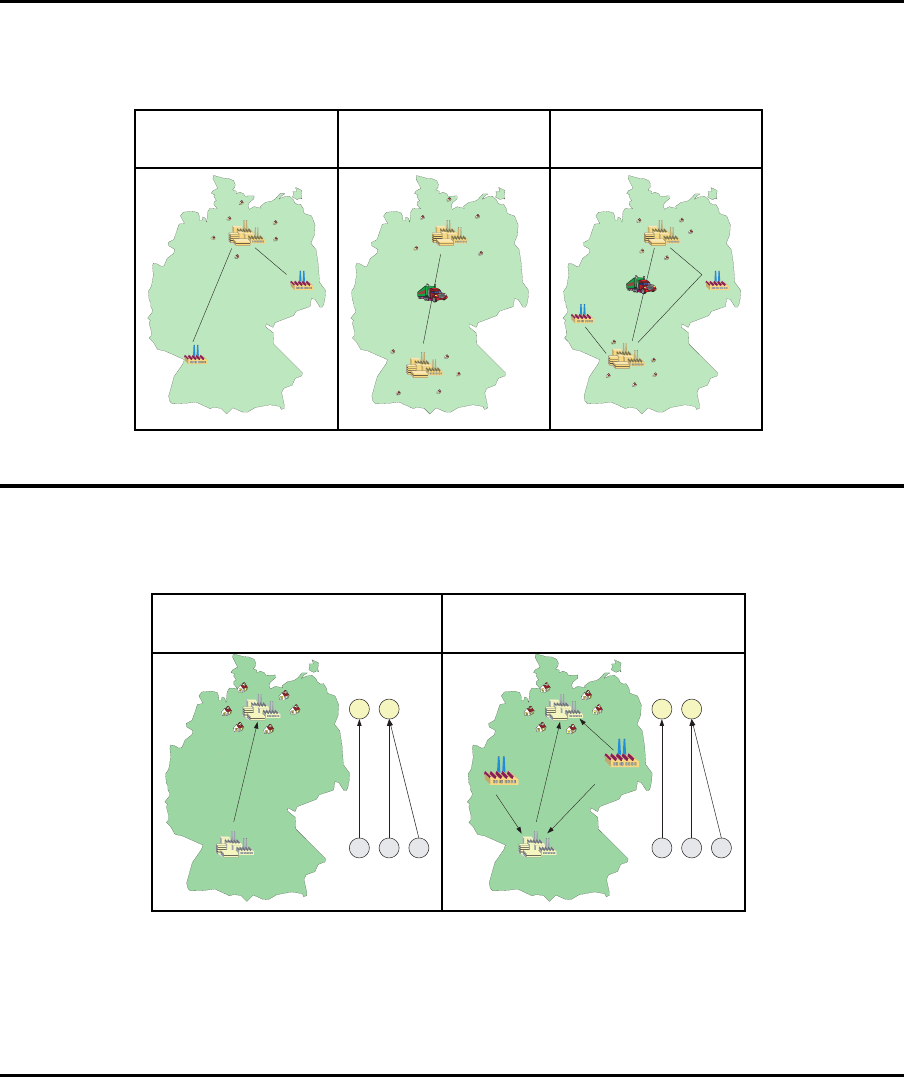
21.5 Modellvarianten
Ein Produktionsstandort
Mehrere
Produktionsstandorte
Ohne Lieferanten Lagerung Lagerung
¨
Uberstun den
¨
Uberstun den
Transporte zwischen
den
Produktionsstandorten
Mit Lieferanten Lagerung Lagerung
¨
Uberstun den
¨
Uberstun den
Beschaffungsmengen
Transporte zwischen
den
Produktionsstandorten
Beschaffungsmengen
157
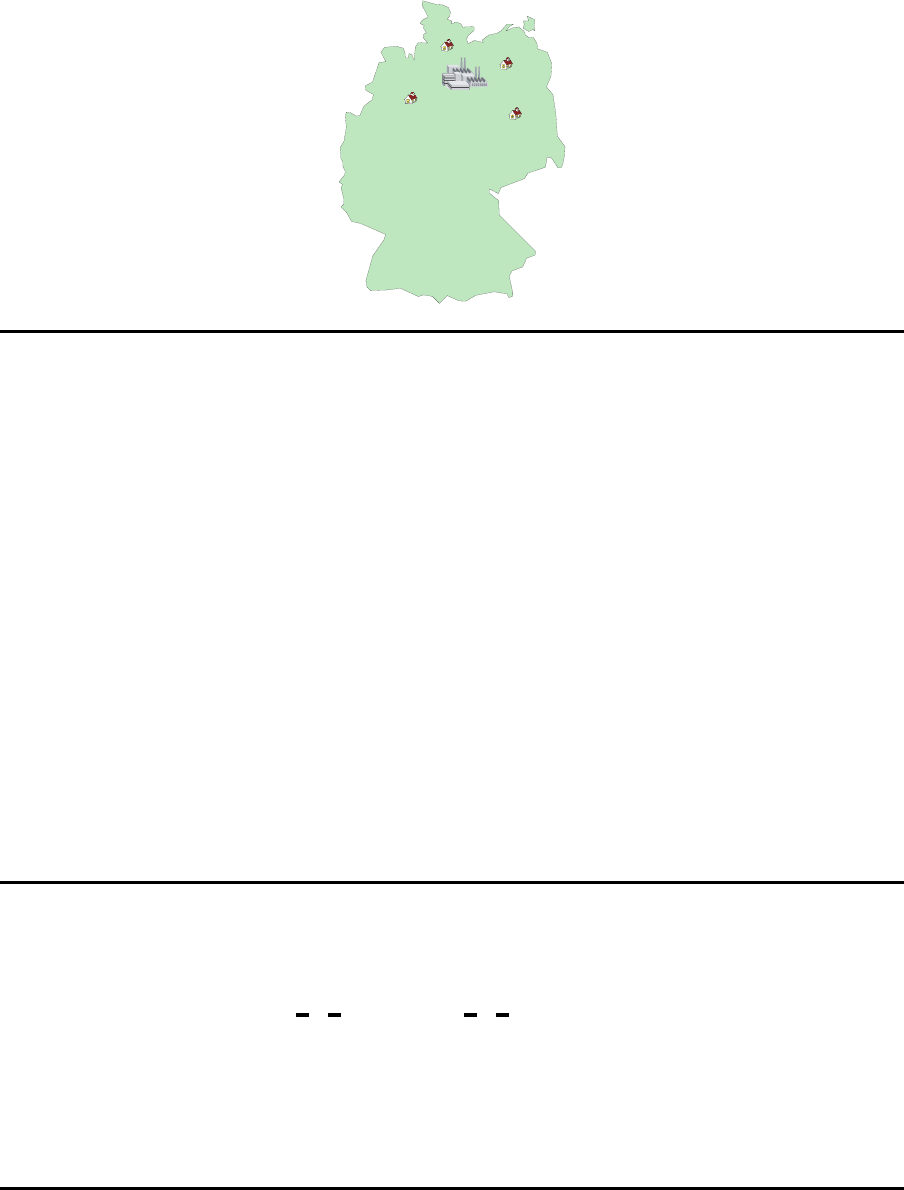
Einstufige Systemstrukt uren
Eine Fabrik Mehrere Fabriken Mehrere Fabriken
Lieferanten Lieferanten
Mehrstufige Systemstrukturen
Mehrere Fabriken Mehrere Fabriken
Lieferanten
Vorprodukte
(Fabrik 2)
Endprodukte
(Fabrik 1)
1 2
a b c
Erzeugnisstruktur
Vorprodukte
(Fabrik 2)
Endprodukte
(Fabrik 1)
1 2
a b c
Erzeugnisstruktur
Lieferanten
Vorprodukte
Endprodukte
Lieferanten
Vorprodukte
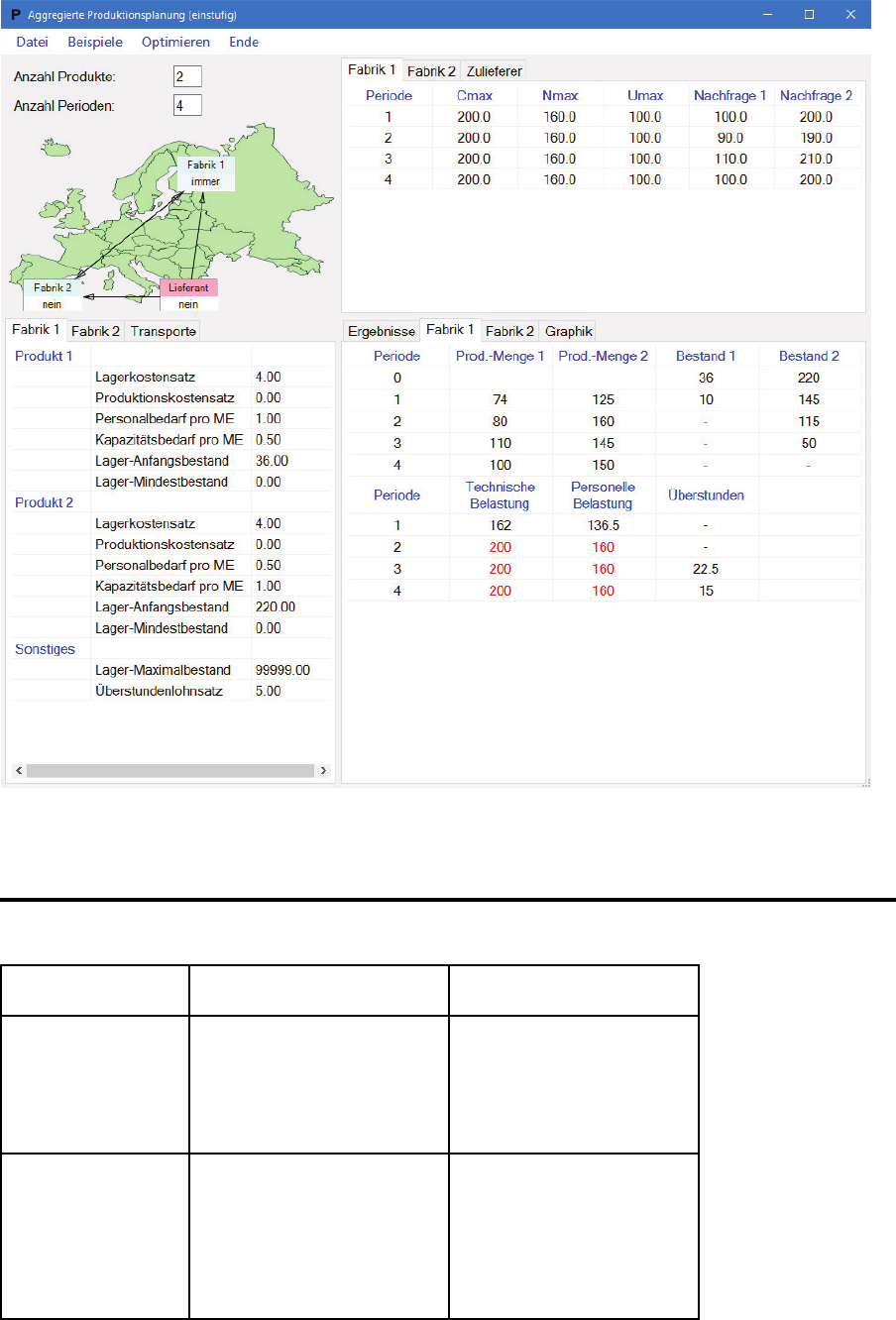
22 Modell 1 – Eine Fabrik
22.1 Annahmen
Modell 1: Eine Fabrik
158
Annahmen
• Eine Fabrik s ∈ S = {1 }.
• Mehrere (End-)Produktgruppen k ∈ K
s
.
• T Perioden (Wochen, Monate, Quartale).
• Produkt- und periodenspezifische Nachfragemengen. Keine explizite Modellierung
der Nachfrager. Der Distributionsprozeß bleibt daher außerhalb der Betrachtung.
• Zielfunktion: Lagerko sten,
¨
Uberstundenkosten
Literaturhinweis
Tempelmeier ( 2018), Aufgabe B1.3
22.2 Modell 1a: Basisversion
Zielfunktion
Min Z =
X
s∈ S
Fabriken
X
k∈K
s
Produkte
T
X
t=1
Perioden
l
s
k
· L
s
kt
| {z }
Lagerkosten
+
X
s∈ S
T
X
t=1
u
s
t
· U
s
t
| {z }
Kosten f¨ur
¨
Uberstunden
159

Lagerbilanzgleichung
L
s
k,t−1
| {z }
Anfangsbestand
+ X
s
kt
|{z}
Produktions-
menge
− L
s
kt
|{z}
Endbestand
= d
s
kt
|{z}
Nachfrage-
menge
s ∈ S; k ∈ K
s
; t = 1, 2, . . . , T
Produktionsmengenbeschr¨ankung f¨ur die technische Kapazit¨at
P
k∈K
s
b
s
k
· X
s
kt
| {z }
technischer
Kapazit¨ats-
bedarf
≤ C
s,max
t
| {z }
technische
Kapazit¨at
s ∈ S; t = 1, 2, ..., T
Produktionsmengenbeschr¨ankung f¨ur die personelle Kapazit¨at
P
k∈K
s
a
s
k
· X
s
kt
| {z }
gesamter
Personal-bedarf
− U
s
t
|{z}
¨
Uberstunden
≤ N
s,max
t
| {z }
verf¨ugbare Nor-
malarbeitszeit
s ∈ S; t = 1, 2, ..., T
maximale
¨
Uberstunden
U
s
t
≤ U
s,max
t
| {z }
maximale
¨
Uberstunden
s ∈ S; t = 1, 2, ..., T
Mindestbestand je Produkt
160

L
s
kt
≥ L
s,min
kt
|{z }
Mindestbestand
s ∈ S; k ∈ K
s
; t = 1, 2, ..., T
Lagerkapazit¨at
X
k∈K
s
L
s
kt
| {z }
Gesamter
Lagerbestand
≤ L
s,max
t
s ∈ S; t = 1, 2, ..., T
Symbole I
Daten
a
s
k
Produktionskoeffizient f¨ur Produkttyp k in bezug auf die pers on elle
Kapazit¨at am Standort s
b
s
k
Produktionskoeffizient f¨ur Produkttyp k in bezug auf die technische
Kapazit¨at am Standort s
C
s,max
t
technische K ap azit¨at in Periode t am Standort s
d
s
kt
Nachfrage f¨ur Produkttyp k in Periode t am Standort s
l
s
k
Lagerkostensatz f¨ur Produkttyp k pro Mengeneinheit und Periode am
Standort s
Symbole II
Daten
N
s,max
t
personelle Kapazit¨at am Stand ort s in Periode t
s Index der Fab riken (in Mod ell nur eine Fabrik s = 1)
S Indexmenge der Fabriken (Vorbereitung f¨ur die folgenden Modelle)
N
s,max
t
personelle Kapazit¨at am Stand ort s in Periode t
U
s,max
t
maximale personelle Zusatzkapazit¨at am Standort s in Perio de t
u
s
t
Kosten f¨ur eine Einheit zus¨atzlicher personeller Kapazit¨at am Standort
s
Symbole III
Variablen
161
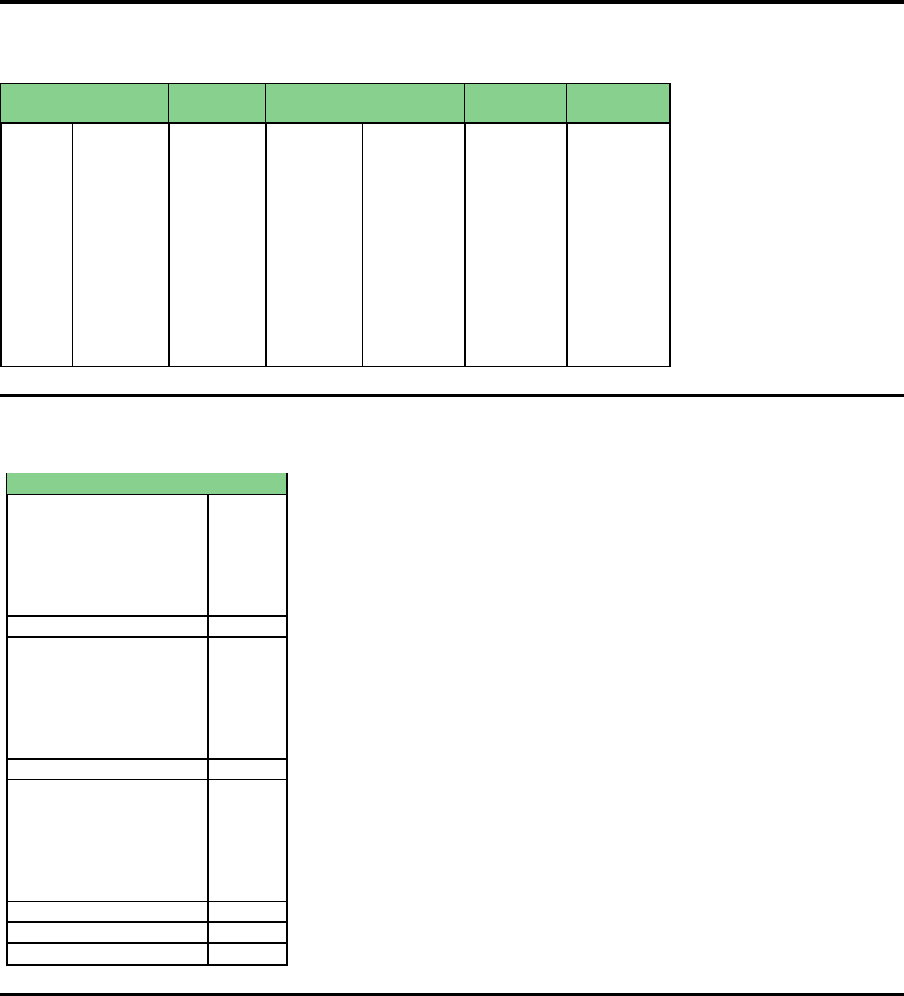
L
s
kt
Lagerbestand f¨ur Produk ttyp k am Standort s am End e von Periode t
U
s
t
genutzte personelle Zusatzkapazit¨at am Standort s in Periode t
X
s
kt
Produktionsm enge von Produkttyp k am Standort s in Periode t
Beispiel: 3 Produkte, 12 Perioden
Periode
Technische
Kapazit¨at
Personelle
Kapazit¨at
Maximale
¨
Uberstunden
Nachfrage 1 Nachfrage 2 Nachfrage 3
1 500.0 260.0 100.0 100.0 200.0 10.0
2 500.0 260.0 100.0 90.0 190.0 140.0
3 500.0 260.0 100.0 60.0 210.0 10.0
4 500.0 260.0 100.0 150.0 200.0 150.0
5 500.0 260.0 100.0 10.0 150.0 100.0
6 500.0 260.0 100.0 50.0 120.0 200.0
7 500.0 260.0 100.0 100.0 100.0 90.0
8 500.0 260.0 100.0 250.0 280.0 50.0
9 500.0 260.0 100.0 60.0 90.0 190.0
10 500.0 260.0 100.0 40.0 50.0 80.0
11 500.0 260.0 100.0 100.0 200.0 90.0
12 500.0 260.0 100.0 180.0 250.0 150.0
Konstanten
Pro dukt 1
Lagerkostensatz 5.00
Pro duktionskostensatz 0.00
Personalbedarf pro ME 1.00
Kapazit¨atsbedarf pro ME 0.50
Lager-Anfangsbestand 36.00
Lager-Mindestbestand 0.00
Pro dukt 2
Lagerkostensatz 5.00
Pro duktionskostensatz 0.00
Personalbedarf pro ME 0.50
Kapazit¨atsbedarf pro ME 1.00
Lager-Anfangsbestand 20.00
Lager-Mindestbestand 0.00
Pro dukt 3
Lagerkostensatz 5.00
Pro duktionskostensatz 0.00
Personalbedarf pro ME 0.80
Kapazit¨atsbedarf pro ME 1.20
Lager-Anfangsbestand 10.00
Lager-Mindestbestand 0.00
Sonstiges
Lager-Maximalbestand 99999.00
¨
Uberstundenlohnsatz 6.00
L¨osung: Mengen
162
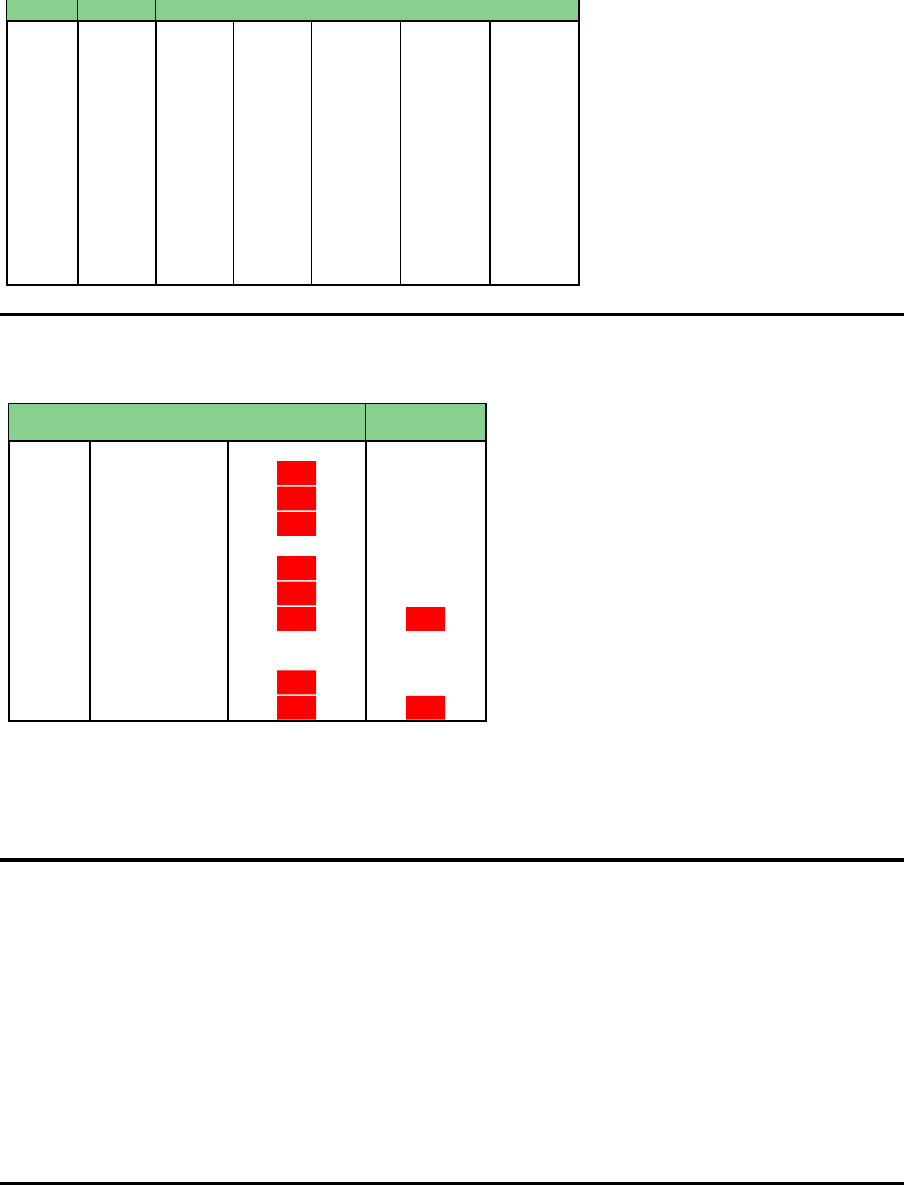
Periode Menge 1 Menge 2 Menge 3 Bestand 1 Bestand 2 Bestand 3
0 36 20 10
1 101 180 - 37 - -
2 53 190 140 - - -
3 147 210 10 87 - -
4 63 200 150 - - -
5 20 150 100 10 - -
6 40 120 200 - - -
7 170 100 90 70 - -
8 180 280 50 - - -
9 60 90 190 - - -
10 117 50 80 77 - -
11 88 200 90 65 - -
12 115 250 150 - - -
L¨osung: Kapazit¨aten
Periode
Technische
Belastung
Personelle
Belastung
¨
Uberstunden
1 230.50 191 -
2 384.50 260 -
3 295.50 260 -
4 411.50 260 23
5 280 175 -
6 380 260 -
7 293 260 32
8 430 260 100
9 348 257 -
10 204.50 206 -
11 352 260 -
12 487.50 260 100
Zielwert = 3260.00
22.3 Modell 1b: Bestandsrestriktionen
Modell 1b
Annahmen
• Es gelten alle Annahmen der Basisversion des Modells 1.
– F¨ur jedes Produkt und jede Periode kann ein Mindestbestand vorgegeben wer-
den.
– F¨ur den gesamten Lagerbestand kann eine Obergrenze vorgegeben werden.
Mindestbestand je Produkt
163
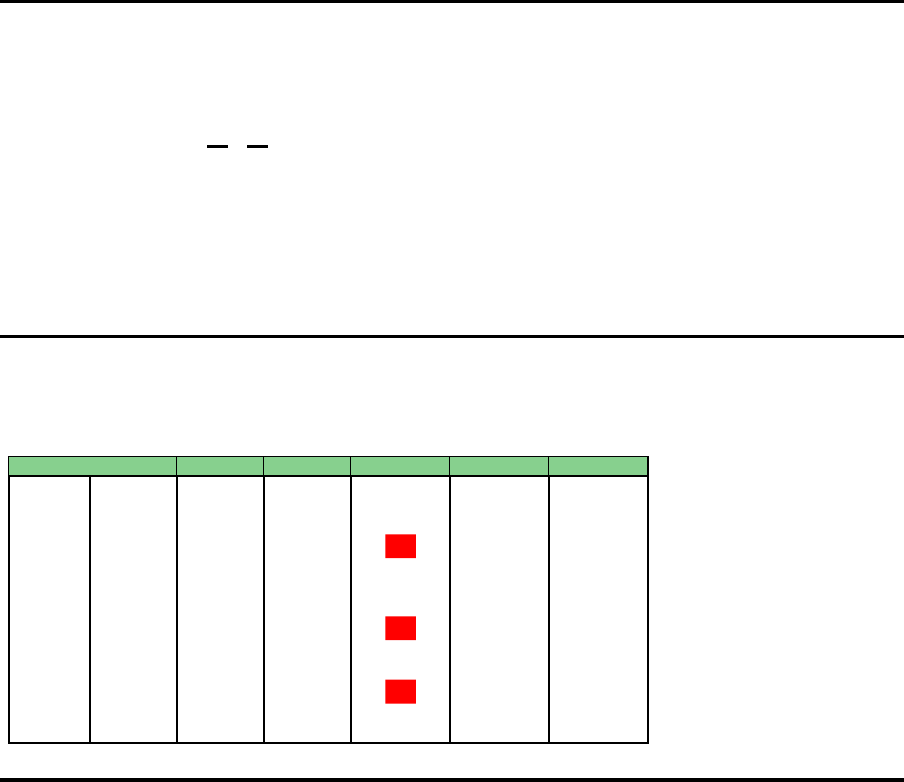
L
s
kt
|{z}
Lagerbestand
f¨ur Produkt k
≥ L
s,min
kt
s ∈ S; k ∈ K
s
; t = 1, 2, ..., T
Lagerkapazit¨at
X
k∈K
s
L
s
kt
| {z }
Gesamt-
Lagerbestand
≤ L
s,max
t
s ∈ S; t = 1, 2, ..., T
Beispiel 2: 3 Produkte, 12 Perioden
L¨osung (Mengen)
Periode Menge 1 Menge 2 Menge 3 Bestand 1 Bestand 2 Bestand 3
0 36 20 10
1 101 180 - 37 - -
2 53 190 140 - - -
3 130 210 10 70 - -
4 80 200 150 - - -
5 20 150 100 10 - -
6 40 120 200 - - -
7 170 100 90 70 - -
8 180 280 50 - - -
9 60 90 190 - - -
10 110 50 80 70 - -
11 95 200 90 65 - -
12 115 250 150 - - -
Beispiel 2: 3 Produkte, 12 Perioden
L¨osung (Kapazit¨a tsbelastung)
164
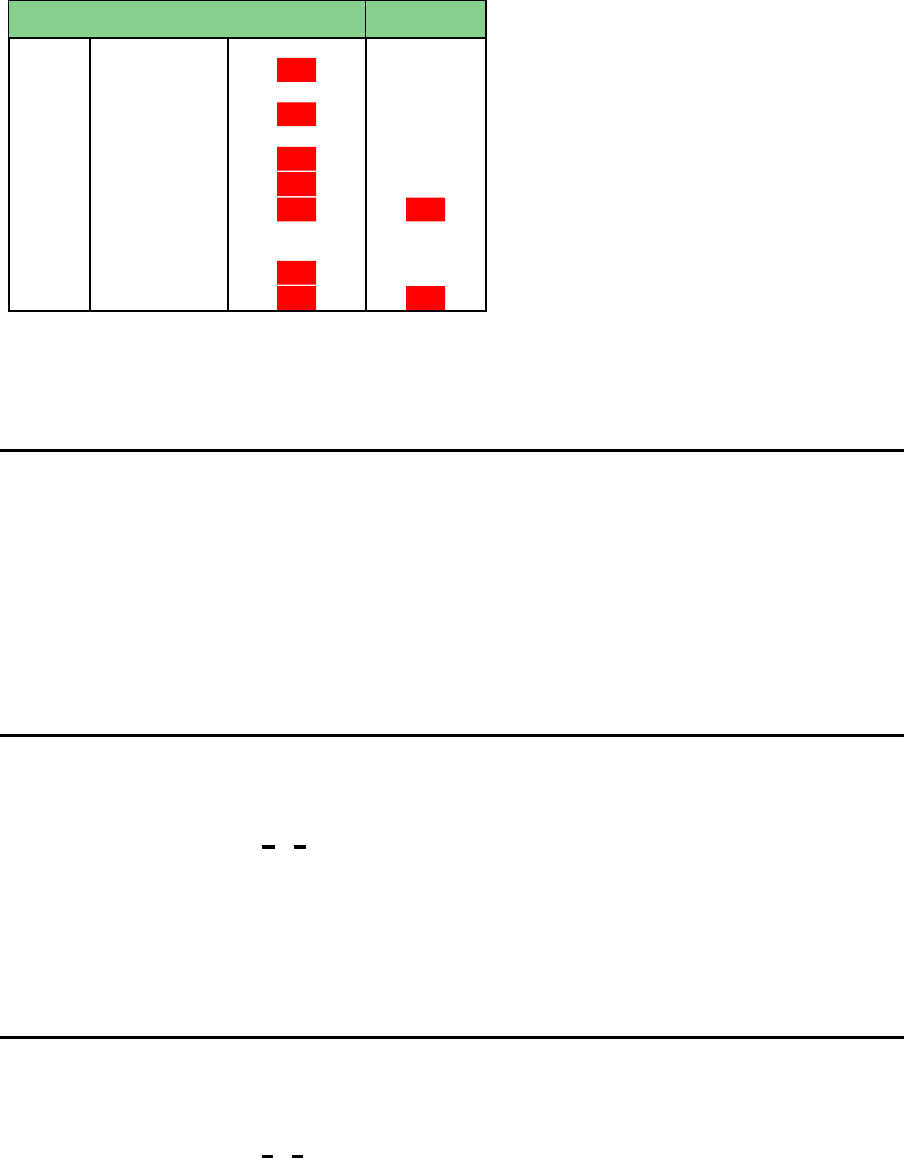
Periode
Technische
Belastung
Personelle
Belastung
¨
Uberstunden
1 230.50 191 -
2 384.50 260 -
3 287 243 -
4 420 260 40
5 280 175 -
6 380 260 -
7 293 260 32
8 430 260 100
9 348 257 -
10 201 199 -
11 355.50 260 7
12 487.50 260 100
Zielwert = 3284.00
22.4 Modell 1c: Mindest¨uberstunden
Modell 1c
Annahmen
• Es gelten alle Annahmen der Basisversion des Modells 1.
– Wenn
¨
Uberstunden in einer Periode t eingeplant werden, dann m¨ussen sie
mindestens U
s,min
t
betragen
Bin¨arvariable setzen
U
s
t
≤ U
s,max
t
| {z }
maximale
¨
Uberstunden
· γ
s
t
|{z}
Bin¨are Variable
s ∈ S; t = 1, 2, ..., T
Wenn
¨
Uberstunden, dann mindestens U
s,min
t
U
s
t
≥ U
s,min
t
| {z }
Mindest-
¨uberstunden
· γ
s
t
|{z}
Bin¨are Variable
s ∈ S; t = 1, 2, ..., T
165

22.5 Modell 1d: Mindestproduktionsmengen
Modell 1d
Annahmen
• Es gelten alle Annahmen der Basisversion des Modells 1.
– Wenn Produktionsmengen f¨ur Produkt k in Periode t in Fabrik s eingeplant
werden, dann m¨ussen sie mindestens X
s,min
kt
betragen
Bin¨arvariable setzen
X
s
kt
≤ M
|{z}
große Zahl
· γ
s
kt
|{z}
Bin¨are Variable
s ∈ S; t = 1, 2, ..., T
Wenn P roduktion, dann mindestens X
s,min
kt
X
s
kt
≥ X
s,min
kt
| {z }
Mindestproduk-
tionsmenge
· γ
s
kt
|{z}
Bin¨are Variable
s ∈ S; t = 1, 2, ..., T
166