
10
19 Flexible Fertigun gssysteme – Optimierung
19.1 Einf¨uhrung
Optimierung
Entscheidungsprobleme
• Zuordnung von Produkten zu Arbeitspl¨anen und Zuordnung von Arbeitsg¨angen zu
Maschinen
Im Vordergrund dieser Problemstellung steht die Festleg ung der Arbeitspl¨ane (Pro-
duktionsverfahren, Operationsfolgen), nach denen ein Produkt im FF-System bear-
beitet werden soll. Die Festlegung der Arbeitspl¨ane der Produkte ist insb. im Hin-
blick auf eine gleichm¨aßige Auslastung der Ressourcen von Bedeutung und wirkt
sich unmittelbar auf die Produktionsrate des FF-Systems aus. Mit Hilfe der Vari-
ablen zur Zuordnung von Produkten und Arbeitspl¨anen kann auch festgelegt wer-
den, ob ein Werkst¨ucktyp ¨uberhaupt in dem betrachteten FF-System bearbeitet
werden soll oder nicht.
• Auswahl der in das FF-System aufzunehmenden Ressourcen
Bei diesen Entscheidungen wird festgelegt, welche Arten von Ressourcen, d. h. Span-
npl¨atze, Maschinen, Fahrzeuge, etc. in welcher Anzahl im FF-System installiert
werden sollen. Die Festlegung dieser Entscheidungsvariablen bestimmt weitgehend
die Kapazit¨at des FF-Systems und damit die durchschnittliche Produktionsmenge.
• Art und Anzahl der Paletten bzw. Werkst¨ucktr¨ager
Sofern die Anzahl der Paletten nicht als unbegrenzt angenommen wird, ist ihre
optimale Anzahl festzulegen. Die Anzahl der in einem FF-System zirkulierenden
Paletten (Werkst¨ucke) bestimmt das Ausmaß, in dem die verf¨ugbare Kapazit¨at der
Ressourcen genutzt wird. Wenn zu wenige Paletten in dem FF-System zirkulieren,
besteht die Gefahr, daß einzelne Maschinen an Materialnachschub leiden. Ist die
Anzahl der Paletten zu hoch, dann tr agen sie zu einer unn¨otigen, unproduktiven
Erh¨ohung des Lagerbestands innerhalb des FF-Systems bei. Zus¨atzlich ist in vielen
FF-Systemen eine Unterscheidung zwischen mehreren Palettentyp en erforderlich.
Optimierung
Modelle
• Arbeitsplanoptimierung
137
Die Arbeitsplanoptimierung bestimmt den Fluß der Werkst ¨ucke durch das FF-
System, indem die gesamte Produktionsmenge einer Produktart a uf alternativ ein-
setzbare Arbeitspl¨ane (Opera t ionenfolgen) aufgeteilt wird oder die Arbeitsg¨ange
alternativ verwendbaren Stationstypen zugeordnet werden. Da das FF-System
bereits bestehen muß, tritt dieser Problemtyp nicht unmittelbar bei der Ko nfi-
gurationsoptimierung auf. Jedoch wird die Arbeitsplanoptimierung in zahlreichen
Entscheidungsmodellen als ein Subproblem betrachtet, dessen L¨osung eine Voraus-
setzung f¨ur die L¨osung des ¨ubergeordneten Problems darstellt. So ist z. B. bei der
Festlegung der Anzahl ersetzender Maschinen a n einer Station zu ber¨ucksichtigen,
nach welchen Arbeitspl¨anen die Produkte das FF-System durchlaufen werden. Eine
¨
Anderung der Arbeitspl¨ane f¨uhrt i. a. auch zu einer
¨
Anderung der Arbeitslast der
Maschinengruppen (Stationen) und hat damit unmittelbar auch Auswirkungen auf
die optimale Anzahl der Maschinen.
Eine typische Fragestellung lautet hier: Sollen alle Werkst¨ucke der Produktart A
ausschließlich nach dem Arbeitsplan A1 bearbeitet werden oder ist eine Aufteilung
auf die Arbeitspl¨ane A1 und A2 in der Weise sinnvoll, daß der Anteil q
1
der
Werkst¨ucke nach Arbeitsplan A1 und der Anteil q
2
nach Arbeitsplan A2 gefertigt
werden?
• Kapazit¨atsoptimierung
Eine Kapazit¨atsoptimierung wird erforderlich, wenn die in das FF-System grund-
s¨atzlich aufzunehmenden Ressourcentypen (z. B. Drehmaschinen, Waschmaschinen,
Spannpl¨atze etc.) b estimmt worden sind. Im Vordergrund der
¨
Uberlegungen steht
nun die Frage, wie vie le Einheiten eines jeden Ressourcentyps installiert werden
sollen. Dabei ist bereits festgelegt worden, nach welchen Arbeitspl¨anen die Pro -
duktarten bearbeitet werden sollen. Es liegt ebenfalls fest, welche Maschinentypen
(Ressourcentypen) welche Arbeitsg¨ange ausf¨uhren sollen. Aufgabe der Modelle
zur Kapazit¨atsoptimierung ist es in dieser Situation, die notwendige Anzahl a n
Ressourcen eines jeden Typs, d.h. die Anzahl der Maschinen pro Station oder die
Anzahl der Transportwagen f¨ur ein Transportsystem zu ermitteln. Modelle zur Ka-
pazit¨atsoptimierung enthalten Ressourcenvariablen und oft auch Palettenvariablen.
Eine typische Fragestellung k¨onnte hier lauten: Werden drei oder vier FTS-Fahrzeu-
ge ben¨ot igt?
• Ressourcenoptimierung
Modelle zur Ressourcenoptimierung dienen zur Vorbereitung der Entscheidung,
welche Typen von Ressourcen prinzipiell in das FF-System aufgenommen werden
sollen. Sie bestimmen sowohl die Art der in das FF-System aufzunehmenden
Maschinen, deren Anzahl als auch ihre Nutzung durch unterschiedliche Arbeit-
spl¨ane. Als Entscheidungsvariablen treten Variablen zur Zuordnung von Arb eit-
spl¨anen zu Produkten sowie Ressourcenvariablen und Palettenvariablen auf. Das
Problem der Ressourcenoptimierung schließt die Bestimmung der Arbeitspl¨ane sowie
die Festlegung der Kapazit¨aten (Anzahl Maschinen je Sta t ion) mit ein. Wird z. B.
ein bestimmter Maschinentyp nicht in das FF-System aufg enommen, dann kann ein
Arbeitsplan, der auf diesen Maschinentyp zugreift, auch nicht ausgew¨ahlt werden.
138
Eine typische Problemstellung der Ressourcenoptimierung lautet: Soll ein uni-
verselles Bearbeitungszentrum oder eine Mehrspindel-Bohrmaschine in das FF-
System aufgenommen werden?
• Produktart- und Ressourcenoptimierung
• Produktionssystem- und Ressourcenoptimierung
• Produktart-, Produktionssystem- und Ressourcenoptimierung
19.2 Arbeitsplanoptimierung (bei unbegrenzter Palettenanzahl)
Das Problem der Arbeitsplanoptimierung besteht da rin, die gesamte Produktionsmenge
einer im FF-System zu fertigenden Produktart auf mehrere alternative Arbeitspl¨ane
(technologische Reihenfolgen, Routen, Operationenfolgen) aufzuteilen. Grundlage dieses
Entscheidungsproblems ist der Tatbestand, daß f¨ur mindestens eine Produktart mehrere
alternativ und/oder kombiniert einsetzbare Arbeitspl¨ane bekannt sind, nach denen die
Werkst¨ucke dieser Produktart im FF -System bearbeitet werden k¨onnen. Jeder Arbeits-
plan beinhaltet einen bestimmten Weg der Werkst¨ucke durch das F F-System und f¨uhrt
zu einer spezifischen Belastung der Ressourcen. F¨ur die weiteren
¨
Uberlegungen kommt
es nicht auf die Reihenfolge der Bearbeitungsvorg¨ange innerhalb eines Arbeitsplans an,
sondern lediglich auf die Bearbeitungszeiten pro Durchlauf eines Werkst¨ucks durch das
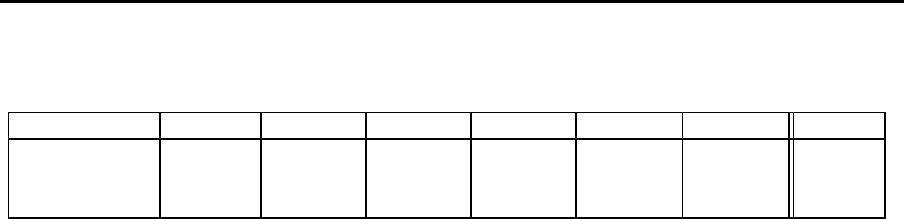
gesamte FF -System. Die folgende Tab elle zeigt drei Arbeitspl¨ane, nach denen eine Pro-
duktart bearbeitet werden kann. Man erkennt, daß die Station ’Dreh-2’ nur dann be-
lastet wird, wenn der Arbeitsplan 2 zum Einsatz kommt. Wird dieser Arbeitsplan nicht
eingesetzt, dann muß die Maschine ’Dreh-2’ auch nicht in die FF-System-Konfiguration
aufgenommen werden.
Alternative Arbeitspl¨ane einer Produktart
mittlere Arbeitsbelastung je Station
Arbeitsplan Spann BAZ-1 BAZ-2 BAZ-3 Dreh-1 Dreh-2 FTS
1 15.00 10.00 5.00 5.00 10.00 – 15.00
2 15.00 – 10.00 30.00 – 5.00 12.00
3 10.00 – 30.00 30.00 – – 9.00
Prinzipiell ist es auch m¨oglich, verschiedene Werkst¨ucke einer Produktart nach unter-
schiedlichen Arbeitspl¨anen bearbeiten zu lassen, z.B. 20% nach Arbeitsplan 1 und 80%
nach Arbeitsplan 2. Diese M¨og lichkeit bietet sich insbesondere dann an, wenn hierdurch
eine gleichm¨aßigere Auslastung der Maschinen des FF-Systems und damit eine h¨ohere
Produktionsrate erzielt werden kann. Die Ber¨ucksichtigung mehrerer Arbeitspl¨ane r
(r = 1, 2, ..., R
k
) f¨ur eine Produktart k ist grunds¨atzlich bereits mit der oben eingef¨uhrten
Darstellung eines FF-Systems m¨oglich. Voraussetzung ist lediglich, daß die Anteile der
Arbeitspl¨ane an der Gesamtproduktionsmenge der Pro duktart k gegeben sein m¨ussen.
Anstelle eines Arbeitsplans f¨ur eine Produktart k werden dann mehrere Arbeitspl¨ane
f¨ur mehrere Dummy-Produktarten k
′
definiert, deren Produktionsmengenanteile α
k
′
sich
zum Produktionsmengenanteil der Produktart k, α
k
, summieren m¨ussen. Im folgenden
139

soll der auf einen Arbeitsplan r der Produktart k bezogene Produktionsmengenanteil
mit q
kr
bezeichnet werden. Modelle zur Arbeitsplanoptimierung betrachten die arbeits-
planbezogenen Produktionsmengenanteile q
kr
als Variablen. Sind f¨ur eine Produktart
k insgesamt R
k
Arbeitspl¨ane gegeben, dann stellt Gleichung (172 ) den Zusammenhang
zwischen den arbeitsplanbezogenen Produktionsmengenanteilen q
kr
und dem gesamten
Produktionsmengenanteil α
k
einer Produktart k her.
Arbeitsplanoptimierung
Arbeitsplanspezifische Produktionsmengenanteile
α
k
=
R
k
X
r=1
q
kr
k = 1, 2, ..., K (172)
w
kmr
= v
kmr
· b
kmr
m = 1, 2, ..., M; r = 1, 2, ..., R
k
; k = 1, 2, ..., K (173)
Wird von einer unbegrenzten Palettenanzahl ausgegangen, dann bedeutet dies, daß die am
h¨ochsten belastete Station des FF-Systems voll ausgelastet ist. Diese Maschine, die den
Engpaß des FF-Systems bildet, muß niemals auf das n¨a chste zu bearbeitende Werkst¨uck
warten, da immer ein unbearbeitetes Werkst¨uck bereits auf das Freiwerden dieser Mas-
chine wart et. Secco-Suardo schl¨agt ein lineares O ptimierungsmodell zur Bestimmung
der optimalen Aufteilung der Produktionsraten der Produkte auf die einzelnen Arbeit-
spl¨ane vor. Ziel ist es dabei, die Produktionsrate des FF-Systems, das mit einer sehr
großen Anzahl von Paletten im S¨attigungsbereich betrieben wird, in Abh¨angigkeit von
der Zuor dnung der Produkte zu den Arbeitspl¨anen zu maximieren. Jede Produktart
k kann nach R
k
Arbeitspl¨anen bearbeitet werden. F¨ur jeden dieser Arbeitspl¨ane r ist
die Arbeitsbelastung der Sta tion m, w
kmr
, beka nnt. Sie kann durch Auswertung der
produktspezifischen Arbeitspl¨ane nach Gleichung (17 3) berechnet werden.
Die Gr¨oßen v
kmr
und b
kmr
unterscheiden sich von den oben definierten Variablen v
km
und
b
km
lediglich durch ihre Bezugnahme auf den Arbeitsplan r. Die Entscheidungsvariablen
des von Secco-Suardo vorgeschlagenen Modells sind die auf die Arbeitspl¨ane bezogenen
Produktionsraten x
kr
der einzelnen Produktarten.
Modell AO-SE (unbegrenzte Anzahl Palett en)
Symbole
140

m Index der Stationen (m = 1, 2, ..., M)
k Index der Produkte (k = 1, 2, ..., K)
r Index der Arbeitspl¨ane (r = 1, 2, ..., R
k
)
α
k
Produktionsmengenanteil der Produktart k
R
k
Anzahl der Arbeitspl¨ane, nach denen Produktart k
bearbeitet werden kann
S
m
Anzahl der Maschinen, Spannpl¨atze, Transportfa hr zeuge etc. an Station m
w
kmr
Arbeitsbelastung der Station m durch den Arbeitsplan r
der Produktart k
X(x) Produktionsrate des FF-Systems
x
kr
Produktionsmenge der Produktart k,
die nach dem Arbeitsplan r produziert wird
Modell AO-SE (unbegrenzte Anzahl Palett en)
Modell
Maximiere X (x) =
K
X
k=1
R
k
X
r=1
x
kr
(174)
u. B. d. R.
R
k
X
r=1
x
kr
= α
k
·
K
X
l=1
R
l
X
r=1
x
lr
k = 1, 2, ..., K (175)
K
X
k=1
R
k
X
r=1
x
kr
· w
kmr
≤ S
m
m = 1, 2, ..., M (176)
x
kr
≥ 0 k = 1, 2, ..., K; r = 1, 2 , ...R
k
(177)
m Index der Stationen (m = 1, 2, ..., M)
k Index der Produkte (k = 1, 2, ..., K)
r Index der Arbeitspl¨ane (r = 1, 2, ..., R
k
)
α
k
Produktionsmengenanteil der Produktart k
R
k
Anzahl der Arbeitspl¨ane, nach denen Produktart k bearbeitet werden kann
S
m
Anzahl der Maschinen, Spannpl¨atze, Transp ortfahrzeuge etc. an Stat ion m
w
kmr
Arbeitsbelastung der Station m durch den Arbeitsplan r der Produktart k
X(x) Produktionsrate des FF-Systems
x
kr
Produktionsmenge der Produktart k, die nach dem Arbeitsplan r
Die Zielfunktion (174) beschreibt die zu maximierende Produktionsrate des gesamten FF-
Systems, d. h. die Summe der Produktionsraten f¨ur alle Produkte ¨uber alle Arbeitspl¨ane.
Die Gleichungen (175) definieren die mengenm¨aßigen Verh¨altnisse der Produktionsraten
141
der verschiedenen Produktarten untereinander. Dabei ist die Summe der Produktions-
raten einer Produktart k ¨uber alle Arbeitspl¨ane gleich dem Produkt aus der Gesamtpro-
duktionsrate des FF-Systems und dem vorgegebenen Produktionsmengenanteil α
k
der
Produktart. Die Neb enbedingungen (176) beschreiben die Kapazit¨atsbeschr¨a nkungen an
den Statio nen. Die mittlere Anzahl besch¨aftigter Maschinen an Station m ergibt sich
aus den mit den Arbeitsbelastungen w
kmr
multiplizierten Produktionsraten. Sie darf die
Anzahl der Maschinen a n der Station nicht ¨uberschreiten. Das Model AO-SE ist ein
kontinuierliches lineares Optimierungsmodell und l¨aßt sich somit z. B. mit dem Simplex-
algorithmus l¨osen. Die Anwendung des Modells AO-SE soll durch ein einfaches Beispiel
erl¨autert werden. Es werden 3 Produkte betrachtet. F¨ur jedes Produkt k sind R
k
ver-
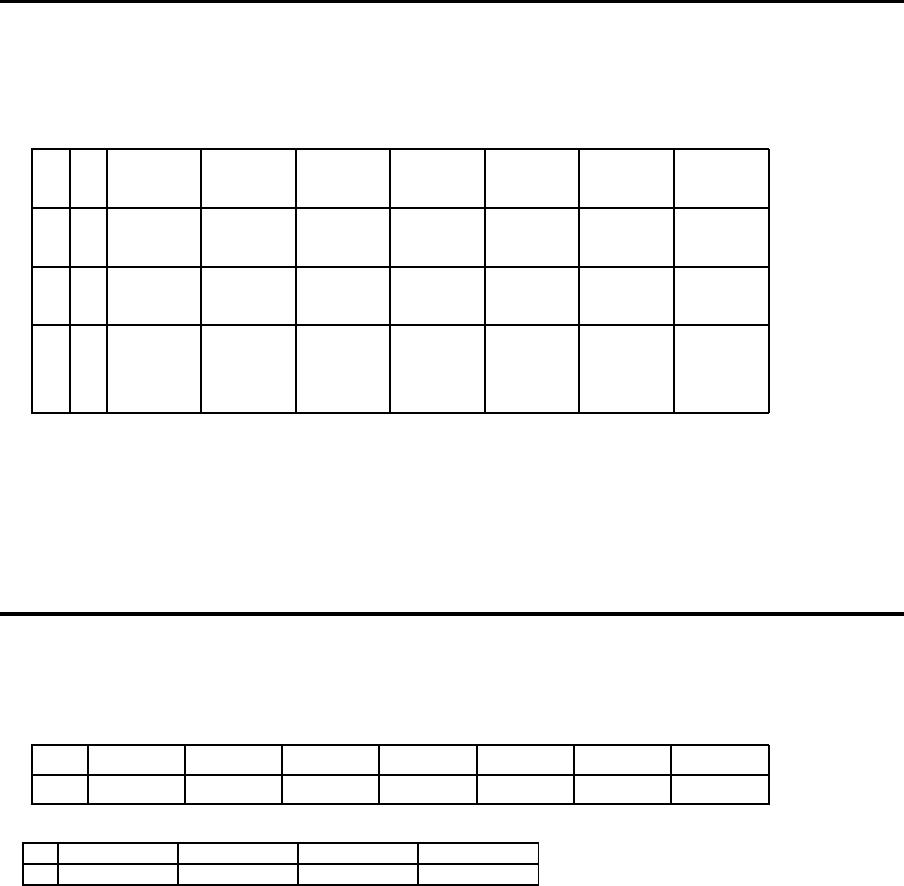
schiedene Arbeitspl¨ane gegeben. In der folgenden Tabelle sind die m¨oglichen Arbeitspl¨ane
zusammengefaßt. Die Angaben in der letzten Spalte (FTS) ergeben sich aus der Anzahl
der durchzuf¨uhrenden Transp orte und der mittleren Fahrzeit von jeweils 3 Minuten.
Arbeitsbelastungen (in Minuten) an den Stationen bei alternativen Arbeit-
spl¨anen
Beispiel 4-1
k r Spann BAZ-1 BAZ-2 BAZ-3 Dreh-
1
Dreh-
2
FTS
1 1 10.00 15.00 30.00 – – – 9.00
2 15.00 20.00 – – 20.00 – 9.00
2 1 5.00 – – 10.00 5.00 16.00 12.00
2 5.00 20.0 0 – – 20.00 – 9.0 0
3 1 15.00 10.00 5.00 5.00 10.00 – 15.00
2 15.00 – 10.00 30.00 – 5.00 12.00
3 10.00 – 30.00 30.00 – – 9.00
In der folgenden Tabelle ist die untersuchte Konfiguration des betrachteten FF-Systems
angegeben, f¨ur die die o ptima le Verteilung der gesamten Produktionsmenge a uf die
verf¨ugbaren Arbeitspl¨ane zu bestimmen ist. Es besteht aus einem Transportsystem mit
drei Fahrzeugen, einer Spannstatio n mit drei Be-/Entladepl¨atzen, verschiedenen Bear-
beitungszentren (BAZ-1, BAZ-2, BAZ-3) und aus zwei Drehzentren (Dreh-1, Dreh-2).
Konfiguration des FF-Systems
(Beispiel 4-1)
Ressourcen
Spann BAZ-1 BAZ-2 BAZ-3 Dreh-1 Dreh-2 FTS
S
m
3 2 2 1 2 2 3
Geplante Produktionsmengenanteile:
k 1 2 3
P
α
k
0.289 0.395 0.316 1.0
LP-Modell:
142

.........................................................................
. . X11 X12 X21 X22 X31 X32 X33 .
.........................................................................
. P-Rate . 1 1 1 1 1 1 1 .
.........................................................................
. Prod-1 . .711 .711 -.289 -.289 -.289 -.289 -.289 = 0 .
. Prod-2 . -.395 -.395 .605 .605 -.395 -.395 -.395 = 0 .
. Prod-3 . -.316 -.316 -.316 -.316 .684 .684 .684 = 0 .
. Spann . 10 15 5 5 15 15 10 <= 3 .
. BAZ-1 . 15 20 20 10 <= 2 .
. BAZ-2 . 30 5 10 30 <= 2 .
. BAZ-3 . 10 5 30 30 <= 1 .
. Dreh-1 . 20 5 20 10 <= 2 .
. Dreh-2 . 16 5 <= 2 .
. FTS . 9 9 12 9 15 12 9 <= 3 .
.........................................................................
Beispiel
Optimale L¨osung
X(k,r) 1 1 0.0554040
X(k,r) 1 2 0.0063990
X(k,r) 2 3 0.0662120
X(k,r) 2 4 0.0182600
X(k,r) 3 5 0.0675770
X(k,r) 3 6 0.0000000
X(k,r) 3 7 0.0000000
X 0.213852
Die arbeitsplanbezogenen Produktionsmengenanteile sind:
q
11
= 0.259 =
0.0554040
0.213852
q
12
= 0.030 =
0.0063990
0.213852
α
1
= 0.289 = 0.259 + 0.030
143

19.3 Ressourcenoptimierung
Das Problem der R essourcenoptimierung besteht darin, neben der Anzahl von Ma-
schinen vor allem auch die Art der Maschinen festzulegen, die in ein FF-System
aufgenommen werden sollen. Offensichtlich in engem Zusammenhang damit steht die
Frage, welche Arbeitsg¨ange in dem FF-System ausgef¨uhrt werden sollen. In der be-
trieblichen Praxis werden derartige
¨
Uberlegungen h¨a ufig angestellt. So wird bisweilen
gepr¨uft, ob eine erg¨anzende Maschine, z. B. eine Waschmaschine, noch als Bestandteil
des FF-Systems eingeplant werden und ¨uber das automatische Transportsystem mit
den anderen Maschinen verbunden werden soll oder ob es g¨unstiger ist, diese Mas-
chine außerhalb des FF-Systems aufzustellen. Das hat dann zur Folge, daß auch der
Arbeitsgang ’Waschen’ aus den auf das FF-System bezogenen Arbeitspl¨anen der Pro-
dukte entfernt werden und extern durchgef¨uhrt werden muß. Derartige
¨
Uberlegungen
k¨onnen offenbar nur ang estellt werden, wenn die technische M¨oglichkeit besteht, alterna-
tive Arbeitspl¨ane vorzusehen. Kommt f¨ur jedes Produkt nur ein Arbeitsplan aufgrund
technischer
¨
Uberlegungen in Betracht, dann kann eine darin enthaltene Maschine auch
nicht aus dem FF-System entfernt werden.
Die unmittelbare
¨
Ubertragung des Modells AO-SE auf die im Rahmen der Ressourcenop-
timierung zu betrachtende Situation, daß die Art und jeweilige Anzahl der in das FF-
System aufzunehmenden Maschinen, Spannpl¨atze und Fahrzeuge noch zu bestimmen ist,
f¨uhrt zu folgendem gemischt-ganzzahligen linearen Optimierungsmodell:
Modell EQS-MIP
unbegrenzte Anzahl Pa l etten
Minimiere Z =
M
X
m=1
C
m
· S
m
+
K
X
k=1
R
k
X
r=1
CO
kr
· x
kr
(195)
u. B. d. R.
R
k
X
r=1
x
kr
= α
k
·
K
X
l=1
R
l
X
r=1
x
lr
k = 1, 2, ..., K (196)
K
X
k=1
R
k
X
r=1
x
kr
·w
kmr
≤ S
m
m = 1, 2, ..., M (197)
Modell EQS-MIP
unbegrenzte Anzahl Pa l etten
K
X
k=1
R
k
X
r=1
x
kr
≥ X
min
(198)
144
x
kr
≥ 0 k = 1, 2, ..., K; r = 1, 2, ..., R
k
(199)
S
m
≥ 0 und ganzzahlig m = 1, 2, ..., M (200)
Zur Veranschaulichung des Modells EQS-MIP betrachten wir das Beispiel 4-4, das durch
Erweiterung des Beispiels 4-1 erzeugt wird. Es wird angenommen, die gew¨unschte Pro-
duktionsrate des FF-Systems sei X
min
= 0.213851 St¨uck/Minute. Weiterhin wird unter-
stellt, daß die Fixkosten pro Ressource, C
m
, gleich den in der folgenden Tabelle angegebe-
nen Werten sind. Lediglich die Kosten einer Maschine an der Station 6 (Dreh-2) wurden
sehr hoch (3000 0 GE) angenommen, damit der Zusammenhang zwischen den Kosten
der Maschinen und dem Einsatz der Arbeitspl¨ane veranschaulicht wird. Von variablen
Produktionskosten wird aus Gr¨unden der Einfachheit abgesehen.
Beispiel 4-4
Kosten der Stationen
1 2 3 4 5 6 7
500 10000 8000 12000 15000 30000 200
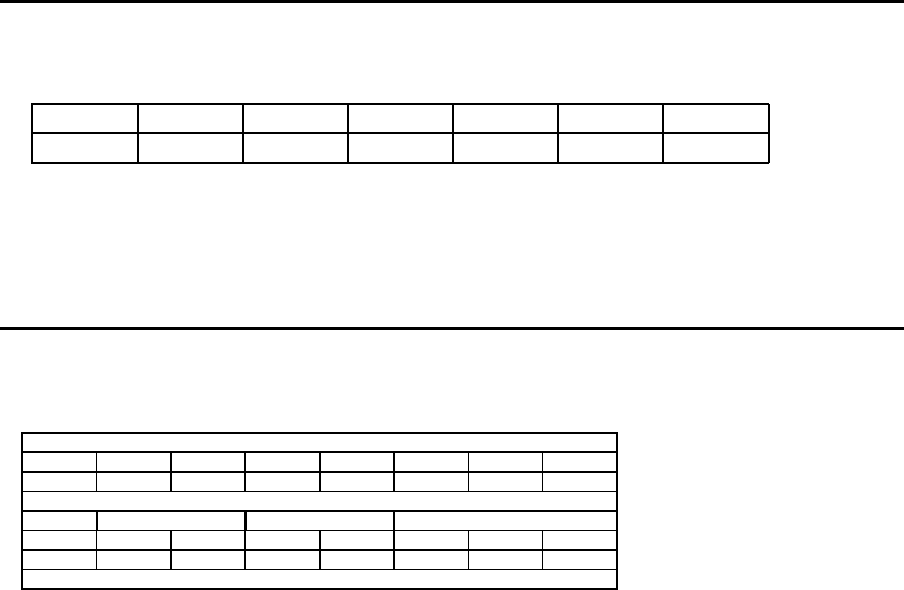
L¨ost man nun das Modell EQS-MIP f¨ur das Beispiel 4-4, dann ergibt sich folgende L¨osung,
deren Kosten 115100 betragen. Die im obigen Modell AO-SE angenommene Anzahl von
Ressourcen f¨uhrt dagegen mit den hier angenommenen Kostens¨atzen zu einem Zielwert
von 140100.
Beispiel 4-4
Optimale L¨osung
Stationen
m 1 2 3 4 5 6 7
S
m
3 4 2 1 3 0 3
Arbeitspl¨ane
k 1 2 3
r 1 2 1 2 1 2 3
x
kr
0.033333 0.028468 0.0 0.084469 0.041090 0.0 0.026485
P
x
kr
= 0.213845
145

19.4 Kapazit¨atsoptimierung
Bei der Konfiguration eines FF-Systems stellt sich regelm¨aßig die Frage, welche Anzahl
von Maschinen eines bestimmten Typs in das FF-System aufgenommen werden soll und
wieviel Paletten in dem F F-System zirkulieren sollen. Wir haben bereits gesehen, daß
von diesen Gr¨oßen ein erheblicher Einfluß auf die Leistung eines FF-Systems ausgehen
kann. Sowohl eine zu geringe Anzahl von Maschinen, Spannpl¨atzen oder Fahrzeugen als
auch eine zu geringe Anzahl von Paletten k¨onnen zur Folge haben, daß ein FF-System
die geforderte Produktionsmenge pro Periode nicht erreicht. Wird zuviel Bearbeitungska-
pazit¨at (Spannpl¨atze, Maschinen, Fahrzeuge) an einer Station vorgesehen, dann bleibt
diese unausgelastet und die Investitionsausgaben f¨ur das FF-System sind h¨oher als das
notwendige Minimum. Zirkulieren zu viele Paletten mit Werkst¨ucken im FF-System,
dann tragen diese nicht mehr wesentlich zu einer Erh¨ohung der Produktionsrate bei,
sondern verbringen die meiste Zeit in Warteschlangen vor den Sta tionen. D a jede einge-
setzte Palette – neben der aus den Anschaffungsauszahlungen resultierenden Kapitalbe-
lastung – mit Lagerbestand (Werkst¨ucke) verbunden ist und zu Platzbedarf in Puffern
f¨uhrt, wird i. d. R. versucht, so wenig Paletten wie m¨oglich im F F-System zirkulieren zu
lassen. Wegen der bestehenden Interdependenzen zwischen der Palettenanzahl und den
Kapazit¨atsauslastungen der einzelnen Stationen ist eine simultane Betrachtung beider
Konfigurationsvariablen erforderlich.
Zur Bestimmung der optimalen Kapazit¨at eines FF-Systems (Systemgr¨oße) schlagen
Vinod und Solberg ein Entscheidungsmodell vor, das die simultane Bestimmung der
optimalen Anzahl an Maschinen, Belade- und Entladestationen, Transportfahrzeugen
und der im FF-System zirkulierenden Paletten zum Gegenstand hat. Die Arbeitspl¨ane
und die Produktionsmengenanteile der Produkte werden als extern gegeben betra chtet
und sind im Gegensatz zu den oben dargestellten Modellen zur Arbeitsplanoptimierung
nun keine Entscheidungsvariablen. Die Zielfunktion des von Vinod und Solberg for-
mulierten Modells umfaßt die vom Investitionsvolumen abh¨angigen Kosten pro Periode
(z. B. kalkulatorische Abschreibungen und Zinsen) sowie die laufenden Kosten des FF-
System-Betriebs. Beide Kostenbestandteile werden als periodenfix in Abh¨angigkeit von
den Anzahl der Maschinen, Spannpl¨atze etc. und der Anzahl zirkulierender Universal-
paletten be-schrieben.
Die so definierten periodenfixen Kosten einer FF-System-Variante sind unter Einhaltung
einer extern vorgegebenen Mindestproduktionsrate X
min
des FF-Systems durch Bestim-
mung der Anzahl Maschinen je Maschinentyp (Station) sowie der Anzahl Spannpl¨atze und
Universalpaletten zu minimieren. Das Entscheidungsmodell bildet damit eine statische
Entscheidungssituation ab und hat folgenden Aufbau:
Modell CA-VS (von Vinod und Solberg)
begrenzte Anzahl Paletten
Minimiere Z(S, N) =
M
X
m=1
C
m
· S
m
+ C
N
· N (182)
146

u. B. d. R.
X(S, N) ≥ X
min
(183)
S
m
, N ≥ 1 und ganzzahlig m = 1, 2, . . . , M (184)
m Index der Stationen (m = 1, 2, ..., M)
C
m
Fixkosten einer Ressource (Maschine, Spannplatz, etc.) an Station m
C
N
Fixkosten einer Universalpalette
X(S, N) Produktionsrate des FF-Systems
X
min
Mindestpro duktionsrate des FF -Systems
N Anzahl Universalpaletten im FF-System
S
m
Anzahl Maschinen, Spannpl¨atze, Fahrzeuge, etc. an Station m
Literaturhinweis
Tempelmeier and Kuhn (1993), Abschnitt 4.3
Das Modell CA-VS zeigt den Z i elkonflikt zwi s chen Maschinenkosten und Palettenkosten.
Mit beiden Ressourcentypen kann man die Produktionsrate beeinflussen.
Wenn man die Anzahl Maschinen S
m
an allen Stationen fixiert, dann kann man die Pro-
duktionsraten f¨ur unterschiedliche Palettenanzahlen mit der Mittelwert- Analyse berech-
nen. Damit kann man dann auch die Mindestanzahl von Paletten bestimmen, die f¨ur die
geforderte Produktionsrate ben¨otigt werden. Das Opt imierungsproblem kann dann auf
die (kombinat orische) Suche nach der optimalen Kombination der Maschinenanzahlen
an den Stationen reduziert werden. Hierzu haben Dallery und Frein ein Suchverfahren
vorgeschlagen.
147