Klassische Bestellmengenformel

Klassische Bestellmenge

Bestellmengenprobleme bzw. Losgrößenprobleme entstehen immer dann, wenn zukünftige Nachfragemengen durch Beschaffungs- oder Produktionsmaßnahmen gedeckt werden müssen und wenn es wegen auftretender fixer Kosten nicht sinnvoll ist, jede auftretende Nachfragemengeneinheit durch einen eigenen Beschaffungs- oder Produktionsvorgang zu decken. In dieser Situation ist es normalerweise sinnvoll, eine größere Menge (Bestellmenge bzw. Losgröße) bereitzustellen und zukünftige Nachfragemengen aus dem auf diese Weise aufgebauten Lagerbestand zu decken. Dies hat den Vorteil, daß fixe Bestellkosten bzw. Produktionskosten eingespart werden. Allerdings sind jetzt Lagerkosten zu berücksichtigen, die durch die Kapitalbindung sowie den Betrieb eines Lagerraums entstehen.

Zwischen die beiden Kostenkomponenten "Fixkosten" und "Lagerkosten" muß nun der optimale Zielkompromiss gefunden werden. Das einfachste Modell geht davon aus, daß die Nachfrage mit einer konstanten Rate pro Zeiteinheit auftritt, z.B. 100 Mengeneinheiten pro Tag. Die Bestellung bzw. Produktion führt zu einem unendlich schnellen Lagerzugang, d.h. der Lagerbestand wird zu Beginn einer Periode bzw. zu einem bestimmten Zeitpunkt aufgefüllt. Weiterhin sind die Fixkosten pro Bestellvorgang, $s$, und die Lagerkosten pro Mengeneinheit und Zeiteinheit, $h$, bekannt.

Die optimale Bestellmenge erhält man, wenn man die Fixkosten und die Lagerkosten pro Zeiteinheit als Funktion der Bestellmenge $Q$ als Gleichung aufschreibt und das Minimum dieser Gleichung bestimmt: Gesamtkosten als Funktion der Bestellmenge $Q$ aufschreiben, 1. Ableitung bilden, Nullsetzen, nach $Q$ auflösen. Das Ergebnis ist die bekannte klassische Wurzelformel zur Bestimmung der kostenminimalen Bestellmenge: $Q_{opt}=\sqrt{\frac{2 \cdot s \cdot D}{h}}$.

Symbole:

$h$	Lagerkostensatz pro Mengeneinheit und Zeiteinheit
$s$	fixer Bestellkostensatz
$D$	durchschnittliche Bedarfsmenge pro Periode
$Q_{opt}$	optimale Bestellmenge

Annahmen:

kontinuierliche und konstante Bedarfsmenge pro Periode
unendlich schneller Lagerzugang
Beschaffungskosten unabhängig von der Bestellmenge Q
es sind keine Fehlmengen erlaubt, d.h. der Lagerbestand darf nicht unter 0 sinken
keine Beschränkungen bzgl. der Bestellmenge Q

Ansicht:

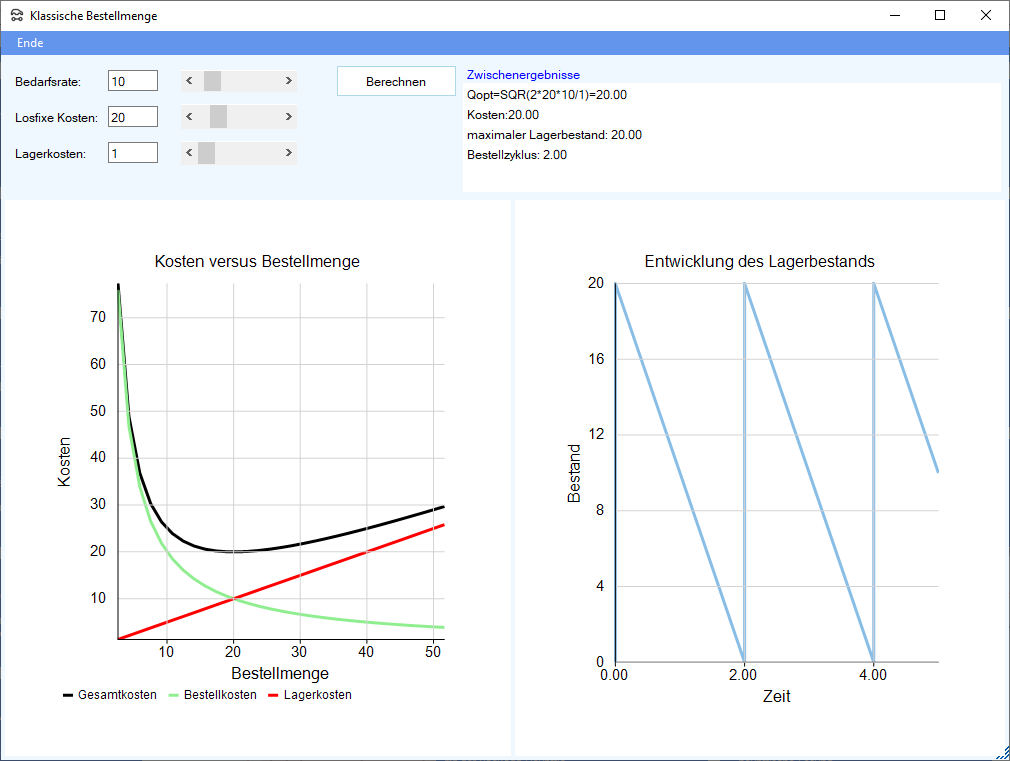
Man sieht, daß exakt an dem Zeitpunkt, an dem der Lagerbestand auf Null gesunken ist, der Bestand wieder auf $Q$ aufgefüllt wird. Dies wiederholt sich unendlich oft.

Literatur:

- Günther/Tempelmeier (2020a)